(Network Analysis)graph centrality measures
Which vertices are important?
(是Youtube上的課程,這兒做筆記學習)
- Graph-theoretic measures:
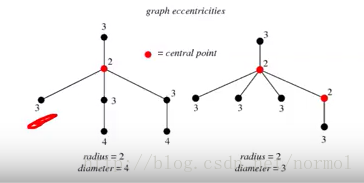
(每個node旁的數字,即這個node的eccentricity,因此diameter就是max(eccentricity),radius就是min(eccentricity),central point是擁有最小的eccentricity的node,圖中標紅的node)
Graph center is a set of vertices with graph eccentricity equal to the graph radius(即center point的集合)
Graph periphery is a set of vertices that have graph eccentricities equal to the graph diameter
(一般理解就是:is those nodes that are far away from the center of the graph)
但以上的這些度量在實際操作中都很難測量,一是因為計算量,二是因為(也是最主要的原因)它們對微小的改變都很敏感。
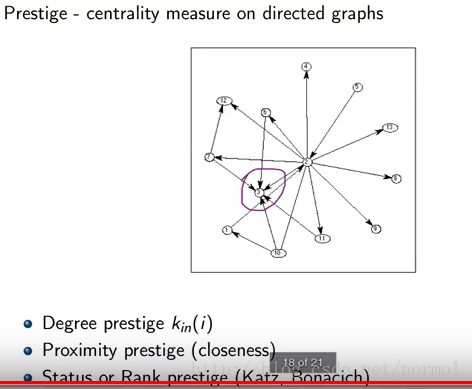
centrality一般指無向圖,
prestige一般指有向圖。
但是現在一般都混用了。
Degree centrality
當需要比較不同圖之間的degree centrality時,需要normalization。
(當沒有標準化時,直接告訴你某個node的的degree centrality是956時沒有任何意義,而標準化之後告訴你degree centrality是0.97,那麼就很明顯的知道,這個node的中心度非常高)Closeness centrality
(但是注意,Closeness centrality只適合計算“connected component”,因為若有一個node是孤立的話,d(i,j)就會無限大,從而會破壞整個公式)
而注意,Harmonic centrality可以避免兩個節點舉例無限大的情況,因為距離無窮大的話,也只會導致一項為0,對總centrality沒有貢獻度而已。因此,實際操作中,這個更常用。Betweenness centrality
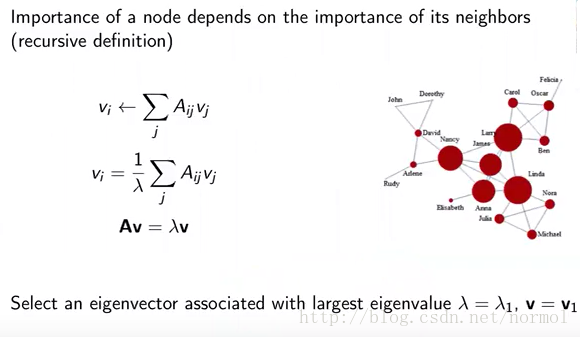
Eigenvector centrality
(之前的degree centrality只考慮了鄰居有多少,而沒有考慮鄰居是誰,而eigenvector centrality就考慮了鄰居是誰的問題)
核心就是:the node is important if node’s neighbors are important
(還要注意的是,pagerank是指的有向圖,而這兒是無向圖)


Katz centrality
(附:
1、注意A代表鄰接矩陣,A^2代表從i-j最短路徑是2的條數,A^3則代表i-j最短路徑是3的條數,後推同理
2、第二行中的vetor e是一個unit vector,其作用就相當於第一行的求和
3、第三行是由於泰勒展開式:
1/(1-k)~=1+k+k^2+……
4、beta將決定最後的k值,當beta=1時,結果將是標準的eigenvector centrality
)
其實,Katz centrality、eigenvector centrality、pagerank的思想都差不多,只不過這兒Katz還可以算鄰居的鄰居,只是距離越大,衰減因數就越大(貢獻越小)Bonacich Centrality
(核心思想:之前的模型都只考慮了“正影響”(positive influence),而沒有考慮negative influence)
當alpha=1,beta=0時,就是標準的eigenvector centrality
當alpha=0,beta>0時,就是Katz centrality
- Centrality example
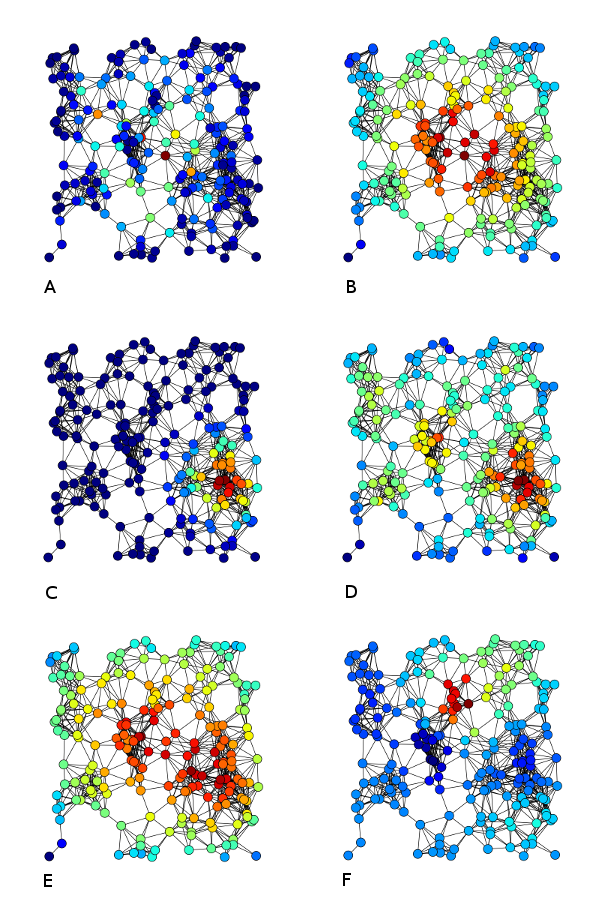
By Tapiocozzo - Own work, CC BY-SA 4.0, Link
A) Betweenness centrality, B) Closeness centrality,
C) Eigenvector centrality, D) Degree centrality,
E) Harmonic Centrality and F) Katz centrality
但這些圖都只是簡單的例子,實際的圖一般來說會是power-law分佈的(可以通過做log-log圖去驗證)
centralization
prestige
Metrics comparison
可以用這些相關係數來衡量上述那麼多centrality衡量metric之間的關係Ranking comparison
concordant & discordant:
分析A:
rank1:A後面是B,rank2也是A後面出現B,於是concordant=1,
rank1:A->C,但rank2中,C出現在A之前,於是discordant=1,
rank1:A->D,rank2:D->A,於是discordant=2,
…..其餘分析同理