學習《Python與機器學習實戰》和《scikit-learn機器學習》時的一些實踐。

隨機漫步

import matplotlib.pyplot as plt
import numpy as np

'''
一維隨機漫步
'''

# 博弈組數
n_person = 2000
# 每組拋硬幣次數
n_times = 500

# 拋硬幣次數序列,用於當繪製點的橫座標
t = np.arange(n_times)
# 一共n_person組,每組是n_times個-1或者1這兩個陣列成的序列表示輸和贏
# 即相當於建立0~1的整數(只有0和1),再*2-1也就是隻有-1和1這兩個數字組成的了
 

steps = 2 * np.random.random_integers(0, 1, (n_person, n_times)) - 1

# np.cumsum返回給定axis上的累計和
# 這裡就是將二維steps的所有列逐步加起來的中間結果
# 這也是一個二維陣列,反映了每組在博弈過程中逐步變化的的輸贏總額
amounts = np.cumsum(steps, axis=1)
# 每個元素平方
sd_amount = amounts ** 2
# 再求所有行(組)的平均值
mean_sd_amount = sd_amount.mean(axis=0)

# Latex
plt.xlabel(
 
r"$t$")
plt.ylabel(r"$\sqrt {\langle (\delta x)^2 \rangle}$")
# 繪製兩條曲線
plt.plot(t, np.sqrt(mean_sd_amount), 'g.', t, np.sqrt(t), 'r-')
plt.show()

執行結果：

埃拉托色尼篩法

import numpy as np

'''
Sieve of Eratosthenes列印1~100中的質數
'''

# 生成從1~100的陣列
a = np.arange(1, 101)

# 該方法最多到開方位置即完成
n_max = int(np.sqrt(len
 
(a)))
# 初始化所有數都設定為"是質數"
is_prime = np.ones(len(a), dtype=bool)
# 1不是質數,2是質數,已經預設設定成True
is_prime[0] = False

for i in range(2, n_max):
    # 如果i是質數
    if i in a[is_prime]:
        # 從i^2開始每次+i的數都因為能被i整除所以不是質數
        is_prime[(i ** 2 - 1)::i] = False
        # 這裡使用從i^2開始,那麼比i小的i的倍數都在前面的迭代中設定過為False了

print(a[is_prime])

執行結果：

[ 2  3  5  7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89
 97]

蒙特卡洛演算法求 $\pi$

import numpy as np

'''
蒙特卡洛演算法求π
'''

# 圓的半徑設定為1,生成100W個點
n_dotes = 1000000
# random.random()生成0和1之間的隨機浮點數
x = np.random.random(n_dotes)
y = np.random.random(n_dotes)
# 計算到圓心(原點)的距離.這裡不對歐氏距離開方,後面只要用半徑r^2=1比較就行
distance = x ** 2 + y ** 2
# 判斷是否在圓內,使用布林索引
in_circle = distance[distance < 1]

pi = 4 * float(len(in_circle)) / n_dotes
print(pi)

執行結果：3.143448

多項式迴歸

import numpy as np
import matplotlib.pyplot as plt

# 使matplotlib正常顯示負號
plt.rcParams['axes.unicode_minus'] = False

BASE_DIR = "E:/WorkSpace/ReadingNotes/Python與機器學習實戰"


# 訓練樣本,利用樣本xs->ys來計算n次多項式係數ps
# 即獲取使得MSE損失即[f(x,p)-y]^2最小的n次多項式係數p的序列
def train(xs, ys, n):
    ps = np.polyfit(xs, ys, n)
    assert len(ps) == n + 1  # 多項式係數從p0~pn,其數目一定是n+1
    return ps


# 以訓練結果ps對指定的xs做預測並獲得預測值
def predict(ps, xs):
    # 對每個x計算多項式SUM{ps[i]*x^(n-i)},i從0到n,即獲得輸入對應的預測值序列
    ys_ = np.polyval(ps, xs)
    return ys_


# 計算MSE損失,即SUM(0.5*[y-y']^2)
def get_mse_loss(ys, ys_):
    return 0.5 * ((ys - ys_) ** 2).sum()


if __name__ == '__main__':
    # 房子面積,房子價格
    xs, ys = [], []
    # 讀入資料
    for line in open(BASE_DIR + "/data/z1/prices.txt"):
        x, y = line.split(",")
        xs.append(float(x))
        ys.append(float(y))
    xs, ys = np.array(xs), np.array(ys)
    # 橫座標(房子面積)標準化
    xs = (xs - xs.mean()) / xs.std()

    fig, ax = plt.subplots(1, 1, figsize=(12, 4))
    ax.scatter(xs, ys, c="k", s=20)  # c=點的顏色,s=點的大小

    # 生成擬合曲線的取樣點
    x0s = np.linspace(-2, 4, 100)
    # 用於擬合數據點的多項式的係數n=1,n=4,n=10
    degs = (1, 4, 10)
    for d in degs:
        # 使用不同次的多項式做訓練,並對取樣點做預測以繪製擬合曲線
        ps = train(xs, ys, d)
        y0s_ = predict(ps, x0s)
        ax.plot(x0s, y0s_, label="多項式次數={}".format(d))
        # 計算在這個訓練結果(ps)下原樣本的MSE損失
        ys_ = predict(ps, xs)
        loss = get_mse_loss(ys, ys_)
        print("多項式次數={},MSE損失={}".format(d, loss))
    # 限制x軸和y軸範圍
    plt.xlim(-2, 4)
    plt.ylim(1e5, 8e5)
    plt.legend()  # 用於顯示圖例
    plt.show()

執行結果：

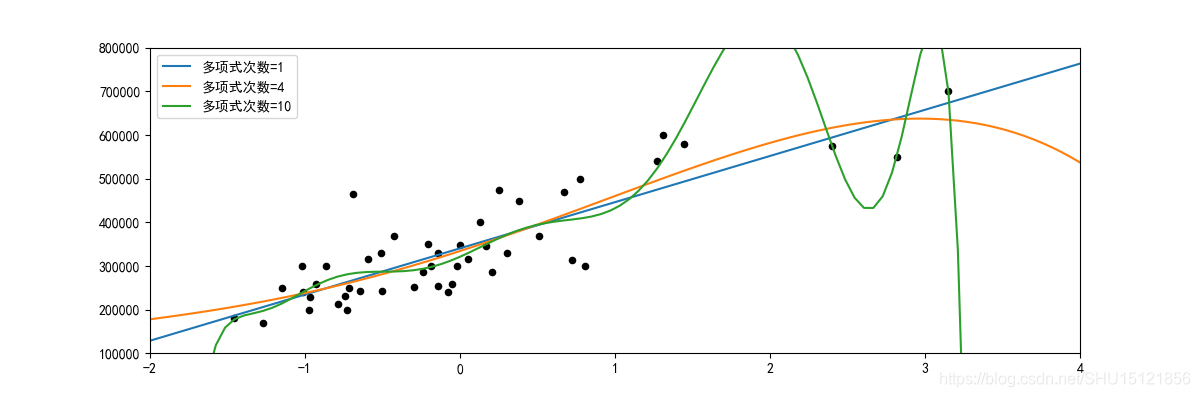
多項式次數=1,MSE損失=96732238800.35297
多項式次數=4,MSE損失=94112406641.6774
多項式次數=10,MSE損失=75874846680.09279

從圖上擬合情況來看，選取次數太高的多項式去擬合數據點顯然會造成嚴重的過擬合。