單應性變換、仿射變換、透視變換
單應性變換
如下圖所示的平面的兩幅影象。紅點表示兩幅影象中的相同物理點,我們稱之為對應點。這裡顯示了四種不同顏色的四個對應點 - 紅色,綠色,黃色和橙色。 一個Homography是一個變換(3×3矩陣),將一個影象中的點對映到另一個影象中的對應點。單應性變換其實就是一個平面到另一個平面的變換關係。

仿射變換
仿射變換是一種二維座標到二維座標之間的線性變換(相同平面),它保持了二維圖形的“平直性”(直線經過變換之後依然是直線)和“平行性”(二維圖形之間的相對位置關係保持不變,平行線依然是平行線,且直線上點的位置順序不變),但是角度會改變。任意的仿射變換都能表示為乘以一個矩陣(線性變換),再加上一個向量 (平移) 的形式。

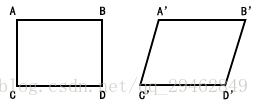
透視變換
透視變換是將圖片投影到一個新的視平面,也稱作投影對映.它是二維(x,y)到三維(X,Y,Z),再到另一個二維
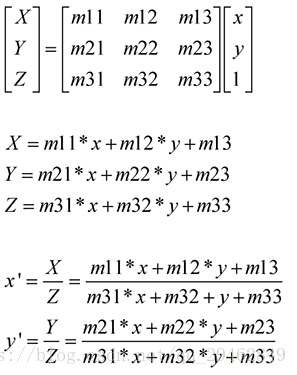

相關推薦
單應性變換、仿射變換、透視變換 很到位
單應性變換 如下圖所示的平面的兩幅影象。紅點表示兩幅影象中的相同物理點,我們稱之為對應點。這裡顯示了四種不同顏色的四個對應點 - 紅色,綠色,黃色和橙色。 一個Homography是一個變換(3×3矩陣),將一個影象中的點對映到另一個影象中的對應點。單應性變換其實就是一
單應性變換、仿射變換、透視變換
單應性變換 如下圖所示的平面的兩幅影象。紅點表示兩幅影象中的相同物理點,我們稱之為對應點。這裡顯示了四種不同顏色的四個對應點 - 紅色,綠色,黃色和橙色。 一個Homography是一個變換(3×3矩陣),將一個影象中的點對映到另一個影象中的對應點。單應性變
OpenCV仿射變換+投射變換+單應性矩陣
arpa title tle 匹配 之間 phy 帶來 http cti OpenCV仿射變換+投射變換+單應性矩陣 本來想用單應性求解小規模運動的物體的位移,但是後來發現即使是很微小的位移也會帶來超級大的誤差甚至錯誤求解,看起來這個方法各種行不通,還是要匹配知道深度
仿射變換透射變換單應性矩陣
estimateRigidTransform():計算多個二維點對或者影象之間的最優仿射變換矩陣 (2行x3列),H可以是部分自由度,比如各向一致的切變。getAffineTransform():計算3個二維點對之間的仿射變換矩陣H(2行x3列),自由度為6.warpAffine():對輸入影象進行仿射變
【影象基礎】相似性變換、放射變換與單應性
本篇博文整合了幾篇博文,意在說明放射變換與透視變換的原理,首先感謝參考文獻中的博主以及還有未提及的博主,如侵犯你的權利請聯絡我刪除 後續博文由於不方便編輯直接給出圖片。具體的文章我寫到有道雲筆記上,連結如下: 平移變換:translation,2個自由度 旋轉變換:ro
【凸優化】保留凸性的幾個方式(交集、仿射變換、投影、線性分式變換)
1. 交集 幾個凸集的交集仍然是凸的 2. 仿射變換 3. 投影(perspective function) 一個投影函式 (perspective function) 的定義是: P(x,t)=x/tdomP={(x,t)∣t>0}
標定中存在的變換(射影變化、仿射變換等)
在標定過程中存在多種物理變換,在這裡進行整理,以便之後使用: 1. 剛性變換 只是物體的位置(平移變換)和朝向(旋轉變換)發生改變,而形狀不變,這樣得到的變換稱為剛性變換。 2. 等距變換 它相當於是平移變換(t)和旋轉矩陣(r)的複合,等距變換前後長度、面積、線線之間的角度都不變,自由
【輔助駕駛】透視變換、仿射變換(包含鳥瞰圖、俯檢視、正檢視)[2]——俯檢視
一、效果 二、程式碼實現 1、python程式碼,基於opencv庫和imutils庫 來源:https://blog.csdn.net/qq_34199383/article/details/79571318 from imutils import perspect
單應性(homography)變換的公式推導過程
原文地址:http://www.cnblogs.com/ml-cv/p/5871052.html 矩陣的一個重要作用是將空間中的點變換到另一個空間中。這個作用在國內的《線性代數》教學中基本沒有介紹。要能形像地理解這一作用,比較直觀的方法就是影象變換,影象變換
【懶懶的計算機視覺筆記之單應性變換】
最近一直在學習Python計算機視覺程式設計中影象到影象之間的對映,這些變化可以用於影象扭曲變形和影象配準。所謂單應性變換就是將一個平面內的點對映到另一個平面內的二維投影變換。單應性變換具有很強的實用性,比如影象配準、影象糾正和紋理扭曲,以及建立全景影象等。其實,單應性變換
單應性變換(Homography)
概要:單應性變換就是一個平面到另一個平面的對映關係。如圖,兩張圖片中相同顏色的點叫做corresponding Points,比如兩個紅點就是一對corresponding points。單應性矩陣(Homography)就是一個從一張影象到另一張影象對映關係的轉換矩陣(3*
單應性變換(Homography)的學習與理解
內容源於:What is Homography ?Consider two images of a plane (top of the book) shown in Figure 1. The red dot represents the same physical poin
直接線性變換(DLT)求解單應性矩陣
在影象拼接中,得到了兩張影象的特徵匹配,兩個點集分別記作X和X′。用單應性變換來擬合二者的關係,可表達為 c⎛⎝⎜uv1⎞⎠⎟=H⎛⎝⎜xy1⎞⎠⎟(1) 其中(uv1)T是X′中特徵點的座標,(xy1)T是X中特徵點的座標,H即是單應性矩陣,代表它們之間的
射影變換與仿射變換、透視變換(射影既透視,包含了Z軸的資訊)
影象處理的仿射變換和透視變換(射影既透視,包含了Z軸的資訊)其實一直也沒理解“仿射”倆字是啥意思,但是大家都這麼叫,其實仿射變換和透視變換更直觀的叫法可以叫做“平面變換”和“空間變換”或者“二維座標變換”和“三維座標變換”。如果這麼命名的話,其實很顯然,這倆是一回事,只不過一
【計算機視覺】【影象處理】幾何變換之仿射變換(平移、縮放、旋轉)
1.概念詞語1)影象的幾何變換 對影象進行放大、縮小、旋轉等操作,會改變原圖中各區域的空間關係,這類操作就是影象的幾何變換。2)仿射變換 對原來的x和y座標分別進行線性的幾何變換,得到新的x和y,這種變換就是放射變換。3)投影變換4)極座標變換5)齊次座標
opencv 影象仿射變換 計算仿射變換後對應特徵點的新座標 影象旋轉、縮放、平移
常常需要最影象進行仿射變換,仿射變換後,我們可能需要將原來影象中的特徵點座標進行重新計算,獲得原來影象中例如眼睛瞳孔座標的新的位置,用於在新得到影象中繼續利用瞳孔位置座標。 關於仿射變換的詳細介紹,請見上面連結的部落格。 我這裡主要介紹如何在已經知道原影象中若干特徵點的
等距變換(歐式變換),相似變換,仿射變換,射影變換
2維空間變換:維數(2*2) 1,等距變換 等距變換是,2維歐式空間變換 ,ε=1,等距變換是保向的,此時是歐氏變換(平移和旋轉的複合)。ε=−1,等距變換是逆向的。 簡單表示 R是正交矩陣。 自由度:3(該變換可以由兩組2D點確定,一組提供兩個自由度) 不
透視變換和仿射變換(下)
其實說白了仿射變換是透視變換的特殊形式,只不過透視變換的角度擴充套件到了z座標,相當於從空間中另一個平面看這個圖,仿射變換在同一個平面不同角度看同一個圖,一下是透視變換的一個例子,通過一個原圖(一個原圖,一個做了相應變換的圖),來確定變換的方位,思想還是上節的思想: 1.通
halcon幾何變換(仿射變換)
ont 關於 pen 範圍 net 算法 handle list 窗口大小 旋轉、平移、鏡像、縮放、斜切,可參考https://blog.csdn.net/machaoyu86/article/details/51182473 仿射變換前,需要獲得仿射變換矩陣。 關於s
Baxter抓取物塊——基於單應性矩陣(二)
之前寫了Baxter抓取物塊的視覺部分(見一),接下來說一說剩下的、比較簡單的模組。 機械臂末端位姿獲取: Baxter啟動後會將自身各座標系的變換關係釋出到 '/tf' 話題中,我們只需要使用TF包(具體參考wiki)即可。定義的cur
