動態規劃公共子問題模式

在解決動態規劃問題時候， 關鍵的一點就是找到子問題， 在動態規劃中有一些常見的子問題模式，需要熟悉。下面就是一些常見子問題模式總結

1. 輸入為x₁,x₂,···, x_n輸出為x₁,x₂, ···, x_i

在這種情況下，子問題是從x1~xi這一部分。
子問題的個數一般為n， 所以用一個dp[n]的陣列就能把子問題的解儲存

例子：LeetCode746 Min Cost Climbing Stairs（爬上樓梯的最小損失）

部落格地址：
https://blog.csdn.net/qq874455953/article/details/82564279

此題利用的就是求當前的dp[i]， 要用到前面的dp[i-1]和dp[i-2]. 也就是說子問題是由前面的x1~xi-1得到的。

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        //定義一個數組 表示爬上每一層樓梯 需要的最少cost
        vector<int> dp(cost.size(), 0);
        //第一層樓梯和第二層樓梯的cost就是本身
        dp[0] = cost[0];
        dp[1
 
] = cost[1];
        //現在迴圈計算 後面每一層的最小cost

        for (int i = 2; i < cost.size(); i++) {
            dp[i] = min(dp[i-2] + cost[i], dp[i-1] + cost[i]);
        }

        //到達樓梯終點的最小cost 就是倒數第一層和第二層的最小cost值
        return min(dp[cost.size()-2] , dp[cost.size()-1]);
    }
};

2. 輸入為x₁,x₂,···, x_n

和y₁,y₂,···, y_n, 輸出為x₁,x₂, ···, x_i和y₁,y₂,···, y_i

在這種情況下， 子問題個數一般為m * n， 所以用dp[m][n] 就能把子問題的解儲存

例子：編輯距離

部落格地址
https://blog.csdn.net/qq_36124194/article/details/83716115

輸入為兩個字串， 也就是x₁ ··· x_m , y₁ ··· y_n ,解的結果是在兩個字串前面的子字串產生。

class Solution {
public:
    int minDistance(string word1, string word2) {
        int size1 = word1.size();
        int size2 = word2.size();
        vector<vector<int>> count(size1+1, vector<int>(size2+1, 0));
        for(int i = 0; i <= size1; i++) {
        	count[i][0] = i;
        }
        for(int i = 0; i <= size2; i++) {
        	count[0][i] = i;
        }

        for(int i = 1; i <= size1; i++) {
        	for(int j = 1; j <= size2; j++) {
        		int tag = 0;
        		if(word1[i-1] != word2[j-1]) {
        			tag = 1;
        		}
        		count[i][j] = min(count[i-1][j]+1, count[i][j-1]+1);
        		count[i][j] = min(count[i][j], tag+count[i-1][j-1]);
        	}
        }
        return count[size1][size2];
    }
};

3. 輸入為x₁,x₂,···, x_n， 輸出為x_i,x_i+1,···, x_j.

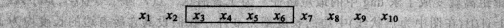
這種情況子問題是 中間的一部分， 所以情況是n*n， 子問題的個數為n^2, 所以用**dp[n][n]**就能把子問題的解儲存

4.輸入為樹, 輸出為子樹

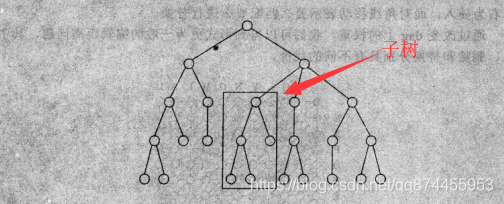
例子：矩陣鏈式相乘

假設有4個矩陣A,B,C,D， 每個矩陣的維度依次是50 * 20， 20 * 1， 1 * 10， 10 * 100， 在計算A * B * C * D 的過程中我們可能會利用矩陣相乘的結合率來優化計算，比如我們可能會這樣計算 (A * B * C) * D 或者 A * ( B * C ）* D ， 會得到很多種計算方式，其中有沒有什麼方式計算量最少呢？

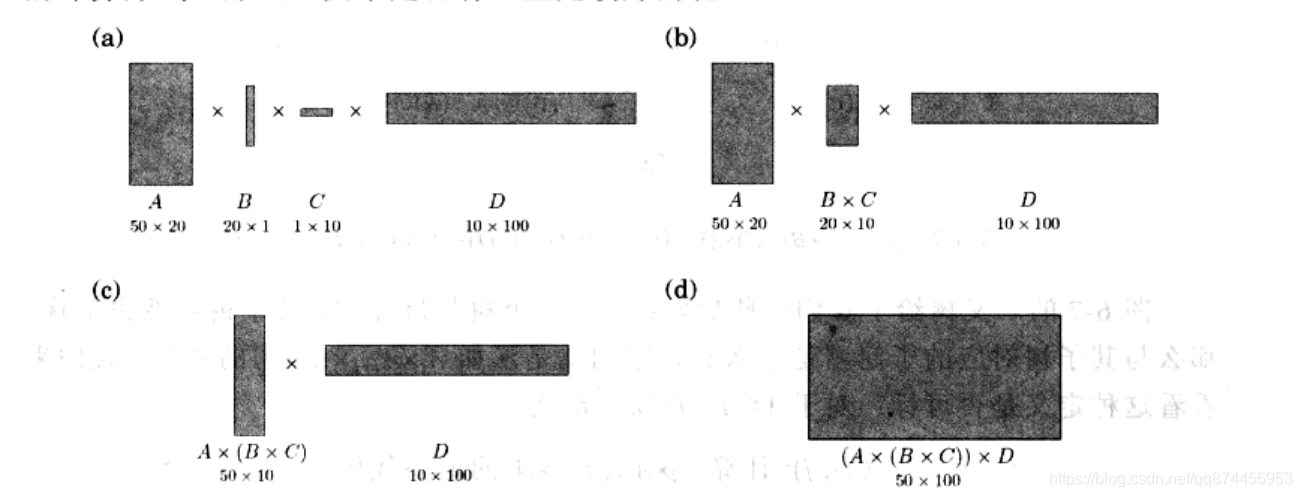
我們可以看到

不同方式會產生巨大差異

其實我們可以把不同的計算順序看成一顆二叉樹， 例如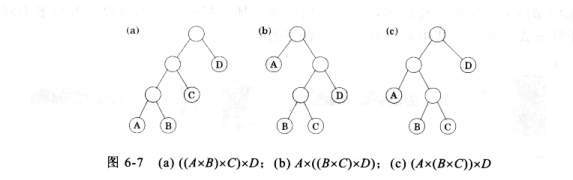

那麼子問題就是這個樹的子樹 動態規劃就變成了求子樹的最優值。