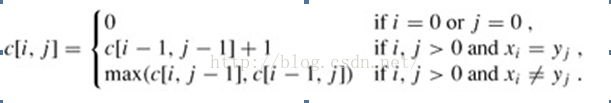編輯距離與最長公共子序列總結
前言:
其實編輯距離和最長公共子序列是對同一個問題的描述,都能夠顯示出兩個字串之間的“相似度”,即它們的雷同程度。而子序列與字串的區別在於字串是連續的,子序列可以不連續,只要下標以此遞增就行。
編輯距離:
Problem description:
設A 和B 是2 個字串。要用最少的字元操作將字串A 轉換為字串B。這裡所說的字元操作包括 (1)刪除一個字元; (2)插入一個字元; (3)將一個字元改為另一個字元。將字串A變換為字串B 所用的最少字元運算元稱為字串A到B 的編輯距離,記為 d(A,B)。試設計一個有效演算法,對任給的2 個字串A和B,計算出它們的編輯距離d(A,B)。
Input
輸入的第一行是字串A,檔案的第二行是字串B。
Output
程式執行結束時,將編輯距離d(A,B)輸出。
Sample Input
fxpimu
xwrs
Sample Output
5
#include<stdio.h>
#include <stdlib.h>
#include <string.h>
int _Min(int a,int b,int c)
{
int min=a;
if (b <min)
min=b;
if(c <min)
min=c;
return min;
}
int ComputeDistance(char s[],char t[])
{
int n = strlen(s);
int m = strlen(t);
//int d[][] = new int[n + 1, m + 1]; // matrix
int **d = (int **)malloc((n+1) * sizeof(int *));
for(int i=0; i<=n; ++i)
{
d[i] = (int *)malloc((m+1) * sizeof(int));
}
// Step 1
if (n == 0)
{
return m;
}
if (m == 0)
{
return n;
}
// Step 2
for (int i = 0; i <= n; i++)
{
d[i][0] =i;
}
for (int j = 0; j <= m; d[0][j] = j++)
{
d[0][j] =j;
}
// Step 3
for (int i = 1; i <= n; i++)
{
//Step 4
for (int j = 1; j <= m; j++)
{
// Step 5
int cost = (t[j-1] == s[i-1]) ? 0 : 1;
// Step 6
d[i][j] = _Min(d[i-1][j]+1, d[i][j-1]+1,d[i-1][j-1]+cost);
}
}
// Step 7
return d[n][m];
}
int main(int argc, char *argv[])
{
char a[9999];
char b[9999];
printf("
scanf("%s",&a);
printf("請輸入字串2\n");
scanf("%s",&b);
int result= ComputeDistance(a,b);
printf("%d\n",result);
system("PAUSE");
return 0;
}
////////////////////
Refrence : Dynamic Programming Algorithm(DPA) for Edit-Distance
編輯距離關於兩個字串s1,s2的差別,可以通過計算他們的最小編輯距離來決定。所謂的編輯距離: 讓s1和s2變成相同字串需要下面操作的最小次數。
1. 把某個字元ch1變成ch2
2. 刪除某個字元
3. 插入某個字元例如s1 = “12433”和s2=”1233”;
則可以通過在s2中間插入4得到12433與s1一致。即 d(s1,s2) = 1 (進行了一次插入操作)
編輯距離的性質計算兩個字串s1+ch1, s2+ch2的編輯距離有這樣的性質:
1. d(s1,””) = d(“”,s1) =|s1| d(“ch1”,”ch2”) =ch1 == ch2 ? 0 : 1;
2. d(s1+ch1,s2+ch2) = min( d(s1,s2)+ ch1==ch2 ? 0 : 1 ,
d(s1+ch1,s2),
d(s1,s2+ch2) );
第一個性質是顯然的。第二個性質: 由於我們定義的三個操作來作為編輯距離的一種衡量方法。於是對ch1,ch2可能的操作只有
1. 把ch1變成ch2
2. s1+ch1後刪除ch1 d =(1+d(s1,s2+ch2))
3. s1+ch1後插入ch2 d =(1 + d(s1+ch1,s2))
對於2和3的操作可以等價於:
_2. s2+ch2後新增ch1 d=(1+d(s1,s2+ch2))
_3. s2+ch2後刪除ch2 d=(1+d(s1+ch1,s2))
因此可以得到計算編輯距離的性質2。複雜度分析從上面性質2可以看出計算過程呈現這樣的一種結構(假設各個層用當前計算的串長度標記,並假設兩個串長度都為 n )
可以看到,該問題的複雜度為指數級別 3的 n次方,對於較長的串,時間上是無法讓人忍受的。分析: 在上面的結構中,我們發現多次出現了(n-1,n-1), (n-1,n-2)……。換句話說該結構具有重疊子問題。再加上前面性質2所具有的最優子結構。符合動態規劃演算法基本要素。因此可以使用動態規劃演算法把複雜度降低到多項式級別。動態規劃求解首先為了避免重複計運算元問題,新增兩個輔助陣列。一. 儲存子問題結果。
M[ |s1| ,|s2| ] , 其中M[ i , j ]表示子串 s1(0->i)與 s2(0->j)的編輯距離二. 儲存字元之間的編輯距離.
E[ |s1|, |s2| ] , 其中 E[ i, j ] = s[i] = s[j] ?0 : 1
三. 新的計算表示式根據性質1得到
M[ 0,0] = 0;
M[ s1i, 0 ] = |s1i|;
M[ 0, s2j ] = |s2j|;
根據性質2得到
M[ i, j ] = min( m[i-1,j-1] + E[ i, j ] ,
m[i, j-1] ,
m[i-1,j] );
複雜度從新的計算式看出,計算過程為i=1 -> |s1|
j=1 -> |s2|
M[i][j] = ……因此複雜度為 O( |s1| * |s2| ),如果假設他們的長度都為n,則複雜度為 O(n^2)
解題程式碼:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int fun(char sa[],char sb[])
{
intlen_a=strlen(sa),len_b=strlen(sb);
chararry[100][100]={0};
inti,j;
inta,b,c,t;
for(i=0;i<=len_a;i++)
{
for(j=0;j<=len_b;j++)
{
if(i==0)arry[i][j]=j;
elseif(j==0)arry[i][j]=i;
else
{
a=arry[i-1][j]+1;
b=arry[i][j-1]+1;
if(sa[i-1]==sb[j-1])c=arry[i-1][j-1];
else c=arry[i-1][j-1]+1;
t=b<c?b:c;
arry[i][j]=a<t?a:t;
};
}
}
return arry[i-1][j-1];
}
int main()
{
intline,i;
intans[100];
char sa[10000],sb[10000],e;
scanf("%d",&line);
e=getchar();
for(i=0;i<line;i++)
{
scanf("%s",sa);
scanf("%s",sb);
ans[i]=fun(sa,sb);
}
for(i=0;i<line;i++)printf("%d\n",ans[i]);
return0;
}
解題思路:
利用動態規劃的方法。建立一個arry[len_a][len_b]的二維陣列,行數和列數皆從0開始,行數n,列數m分別代表字串a的前n個字元,和字串b的前m個字元,arry[n][m]代表字串a的前n個字元和字串b的前m個字元之間的編輯距離。首先初始化二維陣列的第一行和第一列,分別為方格所在列數和行數,讓後按如下方法初始化每一個方格。
arry[i][j]=min{arry[i-1][j]+1,arry[i][j-1]+1,arry[i-1][j-1]+sa[i]!=sb[j]}
整體用公式表達:
編輯距離的應用:
DNA分析
拼字檢查
語音辨識
抄襲偵測
相似度計算
解題方法的改進:DNA分析
http://poj.org/problem?id=3356
題目描述:
脫氧核糖核酸即常說的DNA,是一類帶有遺傳資訊的生物大分子。它由4種主要的脫氧核苷酸(dAMP、dGMP、dCMT和dTMP)通過磷酸二酯鍵連線而成。這4種核苷酸可以分別記為:A、G、C、T。
DNA攜帶的遺傳資訊可以用形如:AGGTCGACTCCA.... 的串來表示。DNA在轉錄複製的過程中可能會發生隨機的偏差,這才最終造就了生物的多樣性。
為了簡化問題,我們假設,DNA在複製的時候可能出現的偏差是(理論上,對每個鹼基被複制時,都可能出現偏差):
1. 漏掉某個脫氧核苷酸。例如把 AGGT 複製成為:AGT
2. 錯碼,例如把 AGGT 複製成了:AGCT
3. 重碼,例如把 AGGT 複製成了:AAGGT
如果某DNA串a,最少要經過 n 次出錯,才能變為DNA串b,則稱這兩個DNA串的距離為 n。
例如:AGGTCATATTCC 與 CGGTCATATTC 的距離為 2
你的任務是:編寫程式,找到兩個DNA串的距離。
【輸入、輸出格式要求】
使用者先輸入整數n(n<100),表示接下來有2n行資料。
接下來輸入的2n行每2行表示一組要比對的DNA。(每行資料長度<10000)
程式則輸出n行,表示這n組DNA的距離。
例如:使用者輸入:
3
AGCTAAGGCCTT
AGCTAAGGCCT
AGCTAAGGCCTT
AGGCTAAGGCCTT
AGCTAAGGCCTT
AGCTTAAGGCTT
則程式應輸出:
1
1
2
【注意】
請仔細除錯!您的程式只有能執行出正確結果的時候才有機會得分!
在評卷時使用的輸入資料與試卷中給出的例項資料可能是不同的。
請把所有函式寫在同一個檔案中,除錯好後,拷貝到【考生資料夾】下對應題號的“解答.txt”中即可。
相關的工程檔案不要拷入。
原始碼中不能使用諸如繪圖、Win32API、中斷呼叫、硬體操作或與作業系統相關的API。
允許使用STL類庫,但不能使用MFC或ATL等非ANSI c++標準的類庫。
例如,不能使用CString型別(屬於MFC類庫),不能使用randomize, random函式(不屬於ANSI C++標準)
結題程式碼:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int fun(charsa[],char sb[])
{
int len_a=strlen(sa),len_b=strlen(sb);
char arry[10000][10000];
int i,j;
int a,b,c,t;
for(i=0;i<=len_a;i++)
{
for(j=0;j<=len_b;j++)
{
if(i==0)arry[i][j]=j;
else if(j==0)arry[i][j]=i;
else
{
a=arry[i-1][j]+1;
b=arry[i][j-1]+1;
if(sa[i-1]==sb[j-1])c=arry[i-1][j-1];
elsec=arry[i-1][j-1]+1;
t=b<c?b:c;
arry[i][j]=a<t?a:t;
};
}
}
return arry[i-1][j-1];
}
int main()
{
int line,i;
int ans[100];
char sa[10000],sb[10000],e;
scanf("%d",&line);
e=getchar();
for(i=0;i<line;i++)
{
scanf("%s",sa);
scanf("%s",sb);
ans[i]=fun(sa,sb);
}
for(i=0;i<line;i++)printf("%d\n",ans[i]);
return 0;
}
解題總結:
1.我好不容易把這個程式編好了,然後又好不容易才發現int arry【10000】【10000】陣列不能定義,估計佔用空間太大,如果定義chararry[1000][1000]程式執行成功。
2.在定義變數的時候(尤其是指標,陣列變數)首先給它賦一個初始值,以防在接下來的程式中沒有賦值但是卻引用了。
3.改進:可以讓arry[10000][10000]動態的用arry[2][10000]生成,因為問題的本質是得到arry[10000][10000]元素就行了,並且根據每個元素生成的原理只需要兩行就行了。
最長公共子序列:
問題描述:
字元序列的子序列是指從給定字元序列中隨意地(不一定連續)去掉若干個字元(可能一個也不去掉)後所形成的字元序列。令給定的字元序列X=“x0,x1,…,xm-1”,序列Y=“y0,y1,…,yk-1”是X的子序列,存在X的一個嚴格遞增下標序列<i0,i1,…,ik-1>,使得對所有的j=0,1,…,k-1,有xij=yj。例如,X=“ABCBDAB”,Y=“BCDB”是X的一個子序列。
考慮最長公共子序列問題如何分解成子問題,設A=“a0,a1,…,am-1”,B=“b0,b1,…,bm-1”,並Z=“z0,z1,…,zk-1”為它們的最長公共子序列。不難證明有以下性質:
(1) 如果am-1=bn-1,則zk-1=am-1=bn-1,且“z0,z1,…,zk-2”是“a0,a1,…,am-2”和“b0,b1,…,bn-2”的一個最長公共子序列;
(2) 如果am-1!=bn-1,則若zk-1!=am-1,蘊涵“z0,z1,…,zk-1”是“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一個最長公共子序列;
(3) 如果am-1!=bn-1,則若zk-1!=bn-1,蘊涵“z0,z1,…,zk-1”是“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一個最長公共子序列。
這樣,在找A和B的公共子序列時,如有am-1=bn-1,則進一步解決一個子問題,找“a0,a1,…,am-2”和“b0,b1,…,bm-2”的一個最長公共子序列;如果am-1!=bn-1,則要解決兩個子問題,找出“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一個最長公共子序列和找出“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一個最長公共子序列,再取兩者中較長者作為A和B的最長公共子序列。
求解:
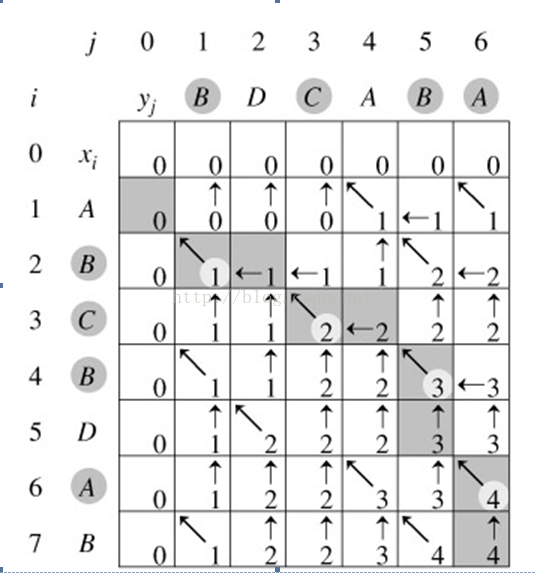
引進一個二維陣列c[][],用c[i][j]記錄X[i]與Y[j] 的LCS 的長度,b[i][j]記錄c[i][j]是通過哪一個子問題的值求得的,以決定搜尋的方向。我們是自底向上進行遞推計算,那麼在計算c[i,j]之前,c[i-1][j-1],c[i-1][j]與c[i][j-1]均已計算出來。此時我們根據X[i] = Y[j]還是X[i] != Y[j],就可以計算出c[i][j]。
問題的遞迴式寫成:
回溯輸出最長公共子序列過程:
演算法分析:由於每次呼叫至少向上或向左(或向上向左同時)移動一步,故最多呼叫(m + n)次就會遇到i = 0或j = 0的情況,此時開始返回。返回時與遞迴呼叫時方向相反,步數相同,故演算法時間複雜度為Θ(m + n)。
程式碼:
#include <stdio.h>#include <string.h>#define MAXLEN 100void LCSLength(char *x,char *y,int m,int n,int c[][MAXLEN],int b[][MAXLEN])...{int i, j;for(i = 0; i<= m; i++)c[i][0] = 0;for(j = 1; j<= n; j++)c[0][j] = 0;for(i = 1;i<= m; i++)...{for(j = 1; j<= n; j++)...{if(x[i-1] == y[j-1])...{c[i][j] = c[i-1][j-1] + 1;b[i][j] = 0;}elseif(c[i-1][j] >= c[i][j-1])...{c[i][j] = c[i-1][j];b[i][j] = 1; }else...{c[i][j] = c[i][j-1];b[i][j] = -1;}}}}void PrintLCS(int b[][MAXLEN],char *x,int i,int j)...{if(i == 0 ||j == 0)return;if(b[i][j]== 0)...{PrintLCS(b, x, i-1, j-1);printf("%c ", x[i-1]);}elseif(b[i][j]== 1)PrintLCS(b, x, i-1, j);elsePrintLCS(b, x, i, j-1);}int main(int argc,char **argv)...{char x[MAXLEN]=...{"ABCBDAB"};char y[MAXLEN]=...{"BDCABA"};intb[MAXLEN][MAXLEN];intc[MAXLEN][MAXLEN];int m, n;m =strlen(x);n =strlen(y);LCSLength(x, y, m, n, c, b);PrintLCS(b, x, m, n);return 0;}
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
int fun(char *sa,char *sb)
{
inti,j,a,b,c,t;
int len_a=strlen(sa)+1,len_b=strlen(sb)+1;
int * arry=(int*)malloc(len_a*len_b*sizeof(int));//配合上文的說明如何用malloc返回值
for(i=0;i<len_a;i++) //強制轉化為二重指標
{
for(j=0;j<len_b;j++)
{
if(i==0||j==0)arry[i*len_b+j]=0;//這是有一種方法
else
{
a=arry[(i-1)*len_b+j];
b=arry[i*len_b+(j-1)];
if(sa[i]==sb[j])c=1;
else c=0;
c=c+arry[(i-1)*len_b+(j-1)];
t=a>b?a:b;
arry[i*len_b+j]=t>c?t:c;
}
}
}
returnarry[(i-1)*len_b+(j-1)];
}
int main()
{
charsa[100];
charsb[100];
gets(sa);
gets(sb);
printf("%d",fun(sa,sb));
return0;
}
程式碼評價:
這個程式只能輸出最長公共子序列的長度,而不能輸出序列。思考如何才能輸出有多個解的最長公共子序列。
動態規劃理解:
我用五個字來總結動態規劃,“最優子結構”,有別於通常說的最有子結構。
“子”:體現了動態規劃最核心的步驟是找物件的子物件,任何事物都是由很多個“子”構成本身這個總體的。如物件是一個字串是,它的“子”可以子串,物件是兩個字串時,它的“子”可以是任意兩個字串的任意組合。具體還是視題意而定。
“最優”:在建立“子”與“子”之間的遞推關係同時,選擇最優解。
“結構”:不僅指“子”解是有一定的結構的,而且還指動態規劃這一方法就是在一定的結構框架內完成的,還要多加參透。
附錄:
題目標題:翻硬幣
小明正在玩一個“翻硬幣”的遊戲。
桌上放著排成一排的若干硬幣。我們用 * 表示正面,用 o 表示反面(是小寫字母,不是零)。
比如,可能情形是:**oo***oooo
如果同時翻轉左邊的兩個硬幣,則變為:oooo***oooo
現在小明的問題是:如果已知了初始狀態和要達到的目標狀態,每次只能同時翻轉相鄰的兩個硬幣,那麼對特定的局面,最少要翻動多少次呢?
我們約定:把翻動相鄰的兩個硬幣叫做一步操作,那麼要求:
程式輸入:
兩行等長的字串,分別表示初始狀態和要達到的目標狀態。每行的長度<1000
程式輸出:
一個整數,表示最小操作步數
例如:
使用者輸入:
**********
o****o****
程式應該輸出:
5
再例如:
使用者輸入:
*o**o***o***
*o***o**o***
程式應該輸出:
1
題目分析:
咋看之下,這道題也是求倆個字串之間的距離,但這道題有它的特殊之處在於操作不一樣。所以我就從找規律的角度去做了,其實編輯距離這道題也能用找規律的方法去做,但是他考慮的情況有非常多種。而這道題不一樣了,通過找規律發現規律很簡單。這道題的演算法可以不歸入五大演算法裡面。
#include<stdio.h>
#include<string.h>
int main()
{
charsa[1000],sb[1000];
intc[1000]={0};
gets(sa);
gets(sb);
intsum=0,i=0,len=strlen(sa),a=0,b=0;
for(i=0;i<len;i++)if(sa[i]!=sb[i])c[i]=1;
for(i=0;i<len;i++)
{
if(c[i]==1)
{
a=i;
for(i=i+1;i<len;i++)if(c[i]==1)
{
b=i;
break;
}
sum+=(b-a);
}
}
printf("%d\n",sum);
return0;
}