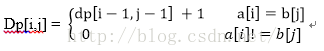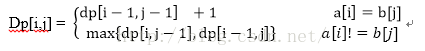動態規劃之子序列與子串問題分析
1、最大子序列
最大子序列是找出由陣列組成的一維陣列中和最大的連續子序列;O(n)
Max = 0 ;
sum = max{a[i]+sum , a[i] };
2、最大升序子序列(LIS:longestincreasing sequence)
最大升序子序列是找出由陣列組成的一維陣列中升序排列最長的可以不連續的子序列;
以A[i]結尾的升序子序列的長度為dis[i]
此處可以記錄下來max取自哪一個Dis[j],結束之後可以倒推最大序列;
3、最長公共子串
兩個字串中最長的公共子串,要求字元連續;
A[n] B[n]記錄dp中的最大值,最大的對角線矩陣就是最長的子串。
4、最長公共子序列(LCS:longest common sequence)
兩個字串中最長的公共子序列,要求字元可以不連續;
A[n] B[n]記錄dp中的最大值,就是最長公共子序列
5、實現方法有兩種,一是遞迴,一是動態規劃;
5.1 遞迴
- 遞迴程式設計簡單,容易理解 效率不高,有大量的重複執行
- 遞迴呼叫,棧開銷比較大
- 只能求出長度,不能求出序列;
5.2 動態規劃
Ø 採用多維陣列來標示中間計算結果,避免重複計算提高效率;
Ø 採用倒推方式可以求出序列;
這是採用空間換時間。
DP輸出結果的時候,一般可以輸出一個結果,如果要輸出多個結果的時候就比較麻煩。需要檢索二維陣列。
int LIS(int *arr , int n ) // O(n*n) { int result = 1 ; int m = 0 ; int *dp = new int[n+1] ; dp[1] = 1 ; for( int i = 2 ;i<=n ;i++) { m = 0 ; for( j = 1 ;j< i ; j++) { if(dp[j] > m && a[j]<a[i]) m = dp[j] ; } dp[i] = m+1 ; if(dp[i] >result) result = dp[i] ; } delete[] dp ; dp = NULL ; return result ; }
這裡的動態陣列可以使用vector實現,先寫到這裡,以後有空再詳細寫一下動歸的思想和具體實現。對於解決這類問題真的是非常好用。
相關推薦
動態規劃之子序列與子串問題分析
1、最大子序列 最大子序列是找出由陣列組成的一維陣列中和最大的連續子序列;O(n) Max = 0 ; sum = max{a[i]+sum , a[i] }; 2、最大升序子序列(LIS:longestincreasing sequence) 最大升序子序列是找出由
動態規劃之最長遞增子序列 最長不重複子串 最長公共子序列
【前言】動態規劃:與分治法相似,即通過組合子問題來求解原問題,不同的是分治法是將問題劃分為互不相交的子問題,遞迴求解子問題,再將他們組合起來求出原問題的解。 動態規劃則應用於子問題重疊的情況,通常用來求解最優化問題。這類問題可以有很多可行解,每個解都有一個值,我們希望尋找最
動態規劃之最長公共子序列&最長公共子串
題目 如果字串1的所有字元按其在字串中的順序出現在另外一個字串2中,則字串1稱之為字串2的子序列。 注意,並不要求子子序列(字串1)的字元必須連續出現在字串2中。 請編寫一個函式,輸入兩個字串,求它們的最長公共子串,並打印出最長公共子序列。 例如:輸入兩個字串BDCA
動態規劃之最長遞增子序列(LIS)
lib sca while -c -o 組成 describe log ret 在一個已知的序列{ a1,a2,……am}中,取出若幹數組成新的序列{ ai1, ai2,…… aim},其中下標 i1,i2, ……im保持遞增,即新數列中的各個數之間依舊保持原
動態規劃之最長公共子序列(LCS)
int tdi -s can 數組下標 include har 遞推 最長公共子序列 在字符串S中按照其先後順序依次取出若幹個字符,並講它們排列成一個新的字符串,這個字符串就被稱為原字符串的子串 有兩個字符串S1和S2,求一個最長公共子串
動態規劃之最長公共子序列
圖片 輔助 length ret %s csp TP 子序列 輸出 原理請參考《算法導論》 定義常量 enum {upper_left, up, left}; #define LENGTHA (sizeof(A)/sizeof(A[0])) #define LENGTHB
動態規劃之----最長公共子序列
什麽是 資料 lcs 由於 main detail span www. 遞歸 一,問題描述 給定兩個字符串,求解這兩個字符串的最長公共子序列(Longest Common Sequence)。比如字符串1:BDCABA;字符串2:ABCBDAB 則這兩個字符串的最長
動態規劃之最長公共子序列(C++原始碼)
動態規劃之最長公共子序列 問題: 在序列X={x1,x2,…,xm}與Y={y1,y2,…,yn}中查詢長度最長的公共子序列,往往不是一個。例如:X={A,B,C,B,D,A,B},Y={B,D,C,A,B,A},則公共子序列有Z={B,C,B,A},Z1={B
動態規劃之最長01子序列問題
問題描述 現在有兩個字串已知 要求的他們最長的公共子序列長度 例如csdnblog和belong的最長公共子序列是4,由於它們都含有blog這一個子序列 解題思路與演算法思想 既然使用動態規劃演算法,那麼演算法的核心就是將問題分佈 這一點和數學
動態規劃之最長上升子序列
問題描述 最長上升子序列(longest increasing subsequence),也可以叫最長非降序子序列,簡稱LIS,不是太難。即一個數的序列bi,當b1 < b2 < … < bS的時候,我們稱這個序列是上升的。對於給定的一個
動態規劃之最長遞增子序列(Longest Increasing Subsequence)
We have discussed Overlapping Subproblems and Optimal Substructure properties in Set 1 and Set 2respectively. 我們已經在前討論了重疊的子問題與最優的子結構屬
hdu1513Palindrome(動態規劃之最長公共子序列變形+滾動陣列)
2題意: 就是填多少字元使之變成迴文字串;#include<iostream> #include<cstring> #include<queue> #include<cstdio> #include<string.h> #include<al
演算法導論——動態規劃之最長公共子序列(LCS)和最長迴文子序列(LPS)
有兩個字串A和B,假設為A=”abcbdab”,B=”bdcaba”;最長公共子序列(LCS)問題指的時找到A和B的一個公共的子串C,C的長度要是最長。 在這裡我們很明顯的發現最長子序列為”bcba” 用動態規劃的思想來考慮這個問題: 若A={a1,a2,
動態規劃——最長公共子序列 與 最長公共子串
1、最長公共子序列LCS 問題,即最長公共子序列問題。它並不要求所求得的字元在所給定的字串中是連續的。比如輸入的兩個字串是 ABCBDAB 和 BDCABA,那麼,BCBA 和 BDAB 都是他們最長的公共子序列。則輸出它們的長度 4。假設兩個字串 A = [A0,A1...
【動態規劃】最長公共子序列與最長公共子串
1. 問題描述 子串應該比較好理解,至於什麼是子序列,這裡給出一個例子:有兩個母串 cnblogs belong 比如序列bo, bg, lg在母串cnblogs與belong中都出現過並且出現順序與母串保持一致,我們將其稱為公共子序列。最長公共子序列(Longest Common Subsequence
[C++] 動態規劃之矩陣連乘、最長公共子序列、最大子段和、最長單調遞增子序列
每次 種子 () return 避免 amp 可能 text com 一、動態規劃的基本思想 動態規劃算法通常用於求解具有某種最優性質的問題。在這類問題中,可能會有許多可行解。每一個解都對應於一個值,我們希望找到具有最優值的解。 將待求解問題分解成若幹個子問題,先求
SDNUOJ 1292 動態規劃之LDS(最長下降子序列)
Description 昨天是平安夜,聖誕老人從房頂上的煙囪裡爬到小朋友床邊把禮物送給夢鄉中的小朋友,但是今年的聖誕老人是處女座的,他有很嚴重的強迫症,他從一條街的一端開始,每次送禮物進的煙囪都不能比之前進的煙囪高,而且他還想要送出最多的禮物。 Input 輸入資料只有一行,該行包含若干個資
動態規劃:最長公共子串 & 最長公共子序列
一、最長公共子串 1. 題目 給定兩個序列 X 和 Y,如果 Z 即是 X 的子串,又是 Y 的子串,我們就稱它是 X 和 Y 的公共子串,注意子串是連續的。 例如 X = { A, B, C, D,
動態規劃之最長單調遞增子序列(C++原始碼)
動態規劃之最長單調遞增子序列 問題: L={a1,a2,a3,…,an}既L是由n個不同的實陣列成的序列,求L的最長單調遞增子序列(下標可不連續)。 分析: 設輔助陣列b,b[i]表示以a[i]為結尾的最長遞增子序列的長度,最長遞增子序列的長度,就是陣列b的最大
動態規劃之longest common subsequence最大公共子序列
這題相對於longest common substring而言更容易一些,區別就子序列和子串, 串的話每個字母是要連續的,序列的話,不要求,用動態規劃做,遞推公式如下,不難: 上程式碼: public class CommonSubseq { public stat