@鋪設道路@

• @題目描述@
• @考場上的思路@
• @比較正常的題解@
• @[email protected]

@題目描述@

春春是一名道路工程師，負責鋪設一條長度為 n 的道路。
鋪設道路的主要工作是填平下陷的地表。整段道路可以看作是 n 塊首尾相連的區域，一開始，第 i 塊區域下陷的深度為 di。

春春每天可以選擇一段連續區間 [L,R]，填充這段區間中的每塊區域，讓其下陷深度減少 1。在選擇區間時，需要保證，區間內的每塊區域在填充前下陷深度均不為 0$。

春春希望你能幫他設計一種方案，可以在最短的時間內將整段道路的下陷深度都變為 0 。

輸入
輸入檔案包含兩行，第一行包含一個整數 n，表示道路的長度。 第二行包含 n 個整數，相鄰兩數間用一個空格隔開，第 i 個整數為 di。

輸出
輸出檔案僅包含一個整數，即最少需要多少天才能完成任務。

輸入樣例#1：
6
4 3 2 5 3 5
輸出樣例#1：
9

樣例解釋1：
一種可行的最佳方案是，依次選擇： [1,6]、[1,6]、[1,2]、[1,1]、[4,6]、[4,4]、[4,4]、[6,6]、[6,6]。

資料規模與約定
對於 30% 的資料，1 ≤ n ≤ 10；
對於 70% 的資料，1 ≤ n ≤ 1000；
對於 100% 的資料，1 ≤ n ≤ 100000 , 0 ≤ di ≤ 10000。

@考場上的思路@

我 抄 我 自 己？
雖然這是 NOIP2013 的原題“積木遊戲”……然而我並沒有做過-_-
所以考場上想了一個比較複雜的解：
顯然觀察樣例，我們可以貪心地這樣做：對於某一個區間，選擇最小值，將這個區間減去這個最小值，然後把區間按照這個最小值分為兩個區間分治求解。
因此，本來想寫線段樹來著……但是我及時地發現（其實是因為不想寫再多想會兒hhhh）區間的最小值是不會變化的。也就是說我們可以不去動態查詢區間最小值，而是建成笛卡爾樹，再在笛卡爾樹上進行操作。

程式碼（不建議參考，建議繼續往後看正常的解）：

#include<cstdio>
#include
 
<stack>
using namespace std;
typedef long long ll;
const int MAXN = 100000;
const int MAXD = 10000;
struct node{
    ll ans; int d;
    node *ch[2];
}tree[MAXN + 5], *tcnt, *NIL, *root;
void init() {
    root = NIL = tcnt = &tree[0];
    NIL->ch[0] = NIL->ch[1] = NIL;
}
node *newnode(int d) {
    tcnt++;
    tcnt->d = d; tcnt->ch[0] = tcnt->ch[1] = NIL;
    return tcnt;
}
stack<node*>stk;
int d[MAXN + 5];
void dfs(node *rt, int x) {
    if( rt == NIL ) return ;
    dfs(rt->ch[0], rt->d);
    dfs(rt->ch[1], rt->d);
    rt->ans = rt->ch[0]->ans + rt->ch[1]->ans + (rt->d - x);
}
int main() {
    init(); int n;
    scanf("%d", &n);
    for(int i=1;i<=n;i++)
        scanf("%d", &d[i]);
    for(int i=1;i<=n;i++) {
        node *nw = newnode(d[i]), *lst = NIL;
        while( !stk.empty() && stk.top()->d > nw->d ) {
            lst = stk.top();
            stk.pop();
        }
        if( !stk.empty() ) stk.top()->ch[1] = nw;
        nw->ch[0] = lst;
        stk.push(nw);
    }
    while( !stk.empty() ) {
        root = stk.top();
        stk.pop();
    }
    dfs(root, 0);
    printf("%lld\n", root->ans);
    return 0;
}

@比較正常的題解@

我們實際上是求如圖的塊的個數。

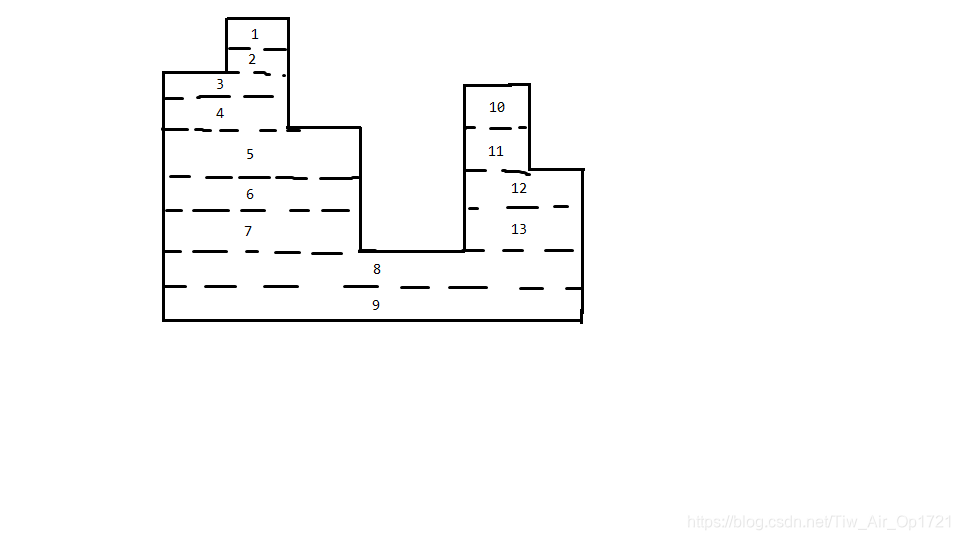
我們不妨在塊的右端點去統計每一塊對答案的貢獻。
所以就很簡單了：
（1）如果 d[i] >= d[i+1]，則 ans+=(d[i]-d[i+1])
（2）如果 d[i] < d[i+1]，則 continue
最後 ans+= d[n] 即可

#include<cstdio>
typedef long long ll;
const int MAXN = 100000;
int d[MAXN + 5];
int main() {
    int n; ll ans = 0;
    scanf("%d", &n);
    for(int i=1;i<=n;i++)
        scanf("%d", &d[i]);
    for(int i=1;i<n;i++)
    	if( d[i] >= d[i+1] ) ans += d[i] - d[i+1];
    ans += d[n];
    printf("%lld\n", ans);
}

@[email protected]

就是這樣，新的一天裡，也請多多關照哦(ノω<。)ノ))☆.。