2. 程式人生 > >決策樹—CART演算法及剪枝處理

決策樹—CART演算法及剪枝處理

阿新 • • 發佈：2018-11-21

前言：上篇博文已經介紹了ID3、C4.5生成決策樹的演算法。由於上文使用的測試資料以及建立的模型都比較簡單，所以其泛化能力很好。但是，當訓練資料量很大的時候，建立的決策樹模型往往非常複雜，樹的深度很大。此時雖然對訓練資料擬合得很好，但是其泛化能力即預測新資料的能力並不一定很好，也就是出現了過擬合現象。這個時候我們就需要對決策樹進行剪枝處理以簡化模型。另外，CART演算法也可用於建立迴歸樹。本文先承接上文介紹完整分類決策樹，再簡單介紹迴歸樹。

四、CART演算法 
CART，即分類與迴歸樹（classification and regression tree），也是一種應用很廣泛的決策樹學習方法。但是CART演算法比較強大，既可用作分類樹，也可以用作迴歸樹。作為分類樹時，其本質與ID3、C4.5並有多大區別，只是選擇特徵的依據不同而已。另外，CART演算法建立的決策樹一般是二叉樹，即特徵值只有yes or no的情況（個人認為並不是絕對的，只是看實際需要）。當CART用作迴歸樹時，以最小平方誤差作為劃分樣本的依據。

1.分類樹 
(1)基尼指數 
分類樹採用基尼指數選擇最優特徵。假設有KK個類，樣本點屬於第kk類的概率為pkpk，則概率分佈的基尼指數定義為


對於給定的樣本集合D，其基尼指數為
這裡，Ck是D中屬於第k類的樣本子集，K是類的個數。 
Python計算如下： 

def calcGini(dataSet):
    '''
            計算基尼指數
    :param dataSet:資料集
    :return: 計算結果
    '''
    numEntries = len(dataSet)
    labelCounts = {}
    for
 
 featVec in dataSet: # 遍歷每個例項，統計標籤的頻數
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys(): 
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    Gini = 1.0
    for key in labelCounts:
        prob = float(labelCounts[key]) / numEntries
        Gini -= prob * prob # 以2為底的對數
 

    return Gini

那麼在給定特徵A的條件下，集合D的基尼指數定義為


基尼指數Gini(D)表示集合D的不確定性，基尼指數Gini(D,A)表示經A=a分割後集合D的不確定性。基尼指數值越大，樣本集合的不確定性也就越大，這一點與熵相似。 
Python計算如下： 

def calcGiniWithFeat(dataSet, feature, value):
    '''
            計算給定特徵下的基尼指數
    :param dataSet:資料集
    :param feature:特徵維度
    :param value:該特徵變數所取的值
    :return: 計算結果
    '''
    D0 = []; D1 = []
    # 根據特徵劃分資料
    for featVec in dataSet:
        if featVec[feature] == value:
            D0.append(featVec)
        else:
            D1.append(featVec)
    Gini = len(D0) / len(dataSet) * calcGini(D0) + len(D1) / len(dataSet) * calcGini(D1)
    return Gini

(2)CART分類樹的演算法步驟如下： 
這裡寫圖片描述
Python實現如下：

def chooseBestSplit(dataSet):
    numFeatures = len(dataSet[0])-1
    bestGini = inf; bestFeat = 0; bestValue = 0; newGini = 0
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        for splitVal in uniqueVals:
            newGini = calcGiniWithFeat(dataSet, i, splitVal)
            if newGini < bestGini:
                bestFeat = i
                bestGini = newGini
    return bestFeat
#     for featVec in dataSet:
#         for splitVal in set(dataSet[:,featIndex].tolist()):
#             newGini = calcGiniWithFeat(dataSet, featIndex, splitVal)
#             if newGini < bestGini: 
#                 bestFeat = featIndex
#                 bestValue = splitVal
#                 bestGini = newGini                


def majorityCnt(classList):
    '''
           採用多數表決的方法決定葉結點的分類
    :param: 所有的類標籤列表
    :return: 出現次數最多的類
    '''
    classCount={}
    for vote in classList:                  # 統計所有類標籤的頻數
        if vote not in classCount.keys():
            classCount[vote] = 0 
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) # 排序
    return sortedClassCount[0][0]


def createTree(dataSet,labels):
    '''
            建立決策樹
    :param: dataSet:訓練資料集
    :return: labels:所有的類標籤
    '''
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList): 
        return classList[0]             # 第一個遞迴結束條件：所有的類標籤完全相同
    if len(dataSet[0]) == 1:        
        return majorityCnt(classList)   # 第二個遞迴結束條件：用完了所有特徵
    bestFeat = chooseBestSplit(dataSet)   # 最優劃分特徵
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}         # 使用字典型別儲存樹的資訊
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]       # 複製所有類標籤，保證每次遞迴呼叫時不改變原始列表的內容
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
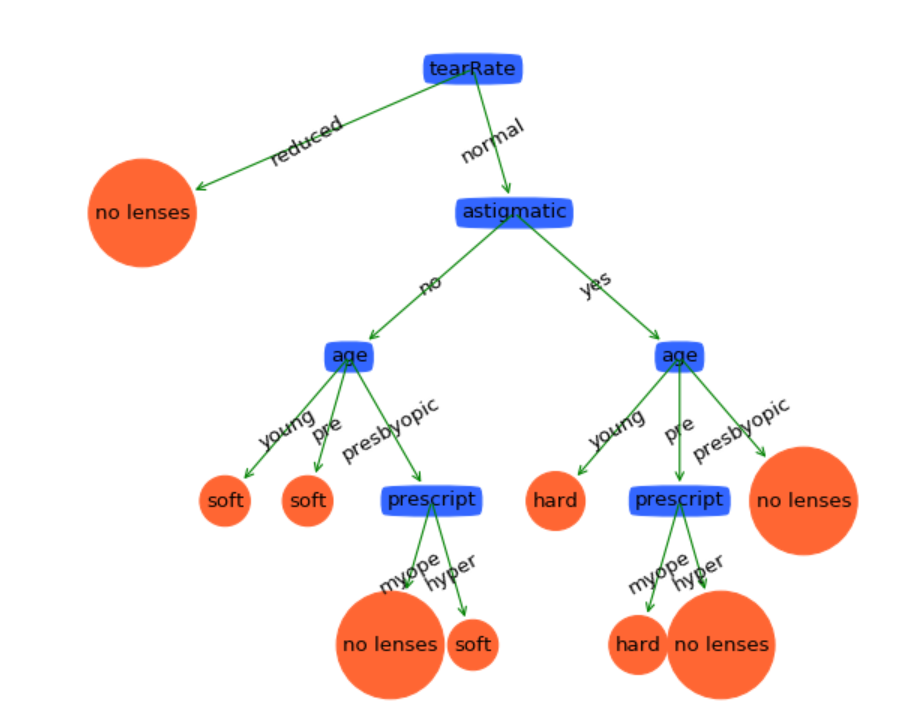
    return myTree

程式碼結構跟上篇博文是基本一樣的，不同的只有選擇特徵的方式。所以就不在此浪費口舌了。我們匯入資料測試一下：

if __name__ == "__main__":
    dataSet,labels = createDataSet()
    subLabels = labels[:]
    myTree = createTree(dataSet, labels)
    print(myTree)
    treePlotter.createPlot(myTree)

這裡寫圖片描述
可見這棵決策樹是非常複雜的。我們可以測試一下它的泛化能力。計算預測誤差的程式碼如下：

# 計算預測誤差 
def calcTestErr(myTree,testData,labels):
    errorCount = 0.0
    for i in range(len(testData)): 
        if classify(myTree,labels,testData[i]) != testData[i][-1]:
            errorCount += 1 
    return float(errorCount)

匯入測試資料：

testData,testLabels = loadTestData()
testErr = calcTestErr(myTree, testData, subLabels)
  • 這裡寫圖片描述 

測試資料集中有6組樣本。由結果可知，有一組樣本預測不正確，那麼預測誤差率為16.7%左右。實際上這個模型並不是很好用的，尤其是在資料量更大的預測集中。此時我們需要簡化這棵決策樹，防止過擬合現象。

2.剪枝（pruning） 
在決策樹學習中將已生成的樹進行簡化的過程稱為剪枝。決策樹的剪枝往往通過極小化決策樹的損失函式或代價函式來實現。實際上剪枝的過程就是一個動態規劃的過程：從葉結點開始，自底向上地對內部結點計算預測誤差以及剪枝後的預測誤差，如果兩者的預測誤差是相等或者剪枝後預測誤差更小，當然是剪掉的好。但是如果剪枝後的預測誤差更大，那就不要剪了。剪枝後，原內部結點會變成新的葉結點，其決策類別由多數表決法決定。不斷重複這個過程往上剪枝，直到預測誤差最小為止。剪枝的實現程式碼如下：

# 計算預測誤差 
def calcTestErr(myTree,testData,labels):
    errorCount = 0.0
    for i in range(len(testData)): 
        if classify(myTree,labels,testData[i]) != testData[i][-1]:
            errorCount += 1 
    return float(errorCount)

# 計算剪枝後的預測誤差
def testMajor(major,testData):  
    errorCount = 0.0  
    for i in range(len(testData)):  
        if major != testData[i][-1]:  
            errorCount += 1   
    return float(errorCount)

def pruningTree(inputTree,dataSet,testData,labels):  
    firstStr = list(inputTree.keys())[0]  
    secondDict = inputTree[firstStr]        # 獲取子樹
    classList = [example[-1] for example in dataSet]  
    featKey = copy.deepcopy(firstStr)  
    labelIndex = labels.index(featKey)  
    subLabels = copy.deepcopy(labels)
    del(labels[labelIndex])  
    for key in list(secondDict.keys()):  
        if isTree(secondDict[key]):
            # 深度優先搜尋,遞迴剪枝
            subDataSet = splitDataSet(dataSet,labelIndex,key)
            subTestSet = splitDataSet(testData,labelIndex,key)
            if len(subDataSet) > 0 and len(subTestSet) > 0:
                inputTree[firstStr][key] = pruningTree(secondDict[key],subDataSet,subTestSet,copy.deepcopy(labels))
    if calcTestErr(inputTree,testData,subLabels) < testMajor(majorityCnt(classList),testData):
        # 剪枝後的誤差反而變大，不作處理，直接返回
        return inputTree 
    else:
        # 剪枝，原父結點變成子結點，其類別由多數表決法決定
        return majorityCnt(classList)

剪枝後的決策樹如下：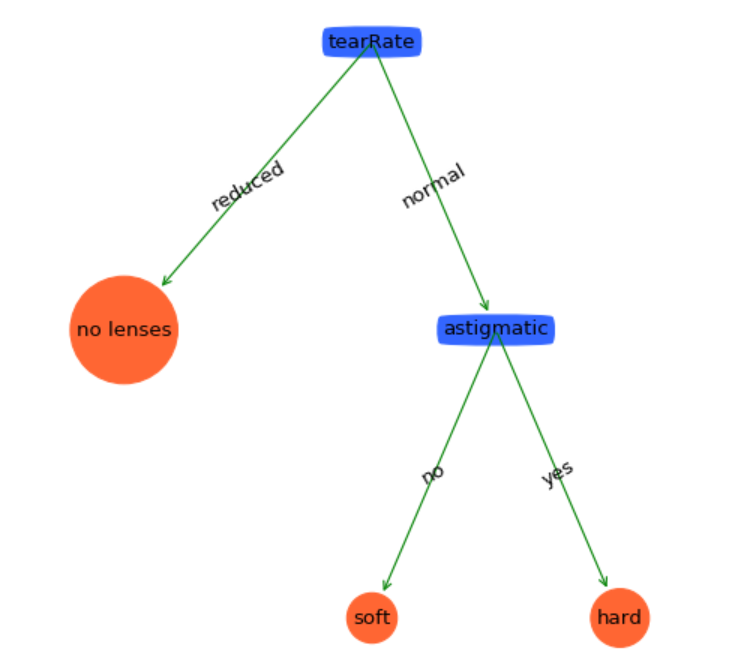 
這裡寫圖片描述 
真的是簡單得太多了。看看它的泛化能力： 
這裡寫圖片描述 
哈哈，預測能力達到100%哦！（這只是一個很小型的測試資料集而已，實際上很少有達到100%泛化能力的模型的。）從這裡可以看出剪枝效果非常好！

3.迴歸樹 
迴歸樹的生成實際上也是貪心演算法。與分類樹不同的是迴歸樹處理的資料連續分佈的。廢話不多說了，直接貼演算法： 
這裡寫圖片描述
CART迴歸樹演算法劃分樣本的依據是最小平方誤差。Python實現如下：

# 生成葉結點
def regLeaf(dataSet):
    return mean(dataSet[:,-1])
# 計算平方誤差
def regErr(dataSet):
    return var(dataSet[:,-1]) * shape(dataSet)[0]

def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
    tolS = ops[0]; tolN = ops[1]
    if len(set(dataSet[:,-1].T.tolist())) == 1: # 停止條件：樣本屬於同一個類
        return None, leafType(dataSet)
    m,n = shape(dataSet)
    S = errType(dataSet)
    bestS = inf; bestIndex = 0; bestValue = 0
    for featIndex in range(n-1):
        for splitVal in set(dataSet[:,featIndex].tolist()):# 固定特徵，併為每個特徵選擇最優二分特徵值
            R0, R1 = binSplitDataSet(dataSet, featIndex, splitVal)
            if (shape(R0)[0] < tolN) or (shape(R1)[0] < tolN): continue
            newS = errType(R0) + errType(R1)
            if newS < bestS: 
                bestIndex = featIndex
                bestValue = splitVal
                bestS = newS
    # 如果誤差下降值小於一個閾值，則不要劃分
    if (S - bestS) < tolS: 
        return None, leafType(dataSet) #exit cond 2
    R0, R1 = binSplitDataSet(dataSet, bestIndex, bestValue)
    if (shape(R0)[0] < tolN) or (shape(R1)[0] < tolN):  # 停止條件:樣本數小於一個閾值
        return None, leafType(dataSet)
    return bestIndex,bestValue

構建迴歸樹如下：

def createTree(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):#assume dataSet is NumPy Mat so we can array filtering
    feat, val = chooseBestSplit(dataSet, leafType, errType, ops)# 選擇最優二分方式
    if feat == None: return val    
    retTree = {}
    retTree['spInd'] = feat
    retTree['spVal'] = val
    leftSet, rightSet = binSplitDataSet(dataSet, feat, val)
    retTree['left'] = createTree(leftSet, leafType, errType, ops)
    retTree['right'] = createTree(rightSet, leafType, errType, ops)
    return retTree

迴歸樹同樣有一個剪枝過程：

def isTree(obj):
    return (type(obj).__name__=='dict')

def getMean(tree):
    if isTree(tree['right']): tree['right'] = getMean(tree['right'])
    if isTree(tree['left']): tree['left'] = getMean(tree['left'])
    return (tree['left']+tree['right'])/2.0

def prune(tree, testData):
    if shape(testData)[0] == 0: return getMean(tree) # 如果沒有測試資料則對樹進行塌陷處理
    if (isTree(tree['right']) or isTree(tree['left'])):
        lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
    # 深度優先搜尋
    if isTree(tree['left']): tree['left'] = prune(tree['left'], lSet)
    if isTree(tree['right']): tree['right'] =  prune(tree['right'], rSet)
    # 到達葉結點
    if not isTree(tree['left']) and not isTree(tree['right']):
        lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
        # 未剪枝的誤差
        errorNoMerge = sum(power(lSet[:,-1] - tree['left'],2)) +\
            sum(power(rSet[:,-1] - tree['right'],2))
        treeMean = (tree['left']+tree['right'])/2.0
        # 剪枝後的誤差
        errorMerge = sum(power(testData[:,-1] - treeMean,2))
        if errorMerge < errorNoMerge: 
            print("merging")
            return treeMean
        else: return tree
    else: return tree

相比線性迴歸，迴歸樹可以對非線性資料建立模型。這個演算法可以使用任意一個測試線性迴歸的資料集來測試，這裡就不再演示了。

五、總結 
總體來講，決策樹模型是一個比較容易理解模型。它建立起來的模型直觀、形象，也比較貼近人們的思維習慣。決策樹更多地用於分類問題而不是迴歸問題。通常，在使用更復雜的演算法之前，一般先建議使用決策樹，並將它的準確率作為效能基準。另外，決策樹還可以幫助我們提取重要特徵。作為機器學習十大演算法之一，決策樹有著它相當重要的地位，基本上市面上能見到的機器學習書籍必定會講這個演算法。然而，決策樹的研究並不止於此。關於決策樹更深的模型有軟決策樹、決策森林、隨機森林等。

分類樹測試資料（包含訓練集和測試集）：http://download.csdn.net/detail/herosofearth/9621052

相關推薦

決策樹—CART演算法及剪枝處理

前言：上篇博文已經介紹了ID3、C4.5生成決策樹的演算法。由於上文使用的測試資料以及建立的模型都比較簡單，所以其泛化能力很好。但是，當訓練資料量很大的時候，建立的決策樹模型往往非常複雜，樹的深度很大。此時雖然對訓練資料擬合得很好，但是其泛化能力即預測新資料的能力並不一定很好，也就是出現了過擬合現象

機器學習演算法（二）——決策樹分類演算法及R語言實現方法

決策樹演算法是分類演算法中最常用的演算法之一。決策樹是一種類似流程圖的樹形結構，可以處理高維資料，直觀易理解，且準確率較高，因此應用廣泛。本篇小博就決策樹的若干演算法：ID3演算法、C4.5演算法以及分類迴歸樹（CART）、C5.0進行對比介紹，並對比C4.5與C5.0處理

機器學習：決策樹cart演算法在分類與迴歸的應用（上）

#include #include #include #include #include #include #include #include #include #include #include using namespace std; //置信水平取0.95時的卡方表 const double CHI

機器學習——十大資料探勘之一的決策樹CART演算法

本文始發於個人公眾號：TechFlow，原創不易，求個關注 今天是**機器學習專題**的第23篇文章，我們今天分享的內容是十大資料探勘演算法之一的CART演算法。 CART演算法全稱是**Classification and regression tree**，也就是分類迴歸樹的意思。和之前介紹

（二）《機器學習》（周誌華）第4章 決策樹 筆記 理論及實現——“西瓜樹”——CART決策樹

cati create def __main__ element iuc 文件 取數 min CART決策樹 （一）《機器學習》（周誌華）第4章 決策樹 筆記 理論及實現——“西瓜樹” 參照上一篇ID3算法實現的決策樹（點擊上面鏈接直達），進一步實現CART決策樹。 其實

決策樹——（三）決策樹的生成與剪枝CART

前面兩篇文章分別介紹了用ID3和C4.5這兩種演算法來生成決策樹。其中ID3演算法每次用資訊增益最大的特徵來劃分資料集，C4.5演算法每次用資訊增益比最大的特徵來劃分資料集。下面介紹另外一種採用基尼指數為標準的劃分方法，CART演算法。 1. CART演算法

【決策樹】熵及ID3演算法Python示例

1、決策樹學習 有如下資料集： 序號 天氣 是否週末 是否有促銷 銷量 1 壞 是 是 高 2 壞 是 是 高 3 壞 是 是 高 4 壞 否 是 高 5 壞 是 是 高 6 壞 否 是 高 7 壞

[Java][機器學習]用決策樹分類演算法對Iris花資料集進行處理

Iris Data Set是很經典的一個數據集，在很多地方都能看到，一般用於教學分類演算法。這個資料集在UCI Machine Learning Repository裡可以找到（還是下載量排第一的資料喲）。這個資料集裡面，每個資料都包含4個值(sepal len

決策樹相關演算法——Bagging之基於CART的隨機森林詳細說明與實現

1 前言 1.1 本篇部落格主要記錄的是基於CART決策樹實現的隨機森林演算法，主要是從以下四個方面介紹: CART決策樹的構建思想；整合學習中的Bagging思想；基於CART決策樹的隨機森林程式碼實現；隨機森林不易過擬合的分析。(其中不易過擬合併不是說隨機

《機器學習》（周誌華）第4章 決策樹 筆記 理論及實現——“西瓜樹”

取數據 dataset 結點 （六） eight dot 都是 ret 集合 參考書籍：《機器學習》（周誌華） 說 明：本篇內容為讀書筆記，主要參考教材為《機器學習》（周誌華）。詳細內容請參閱書籍——第4章 決策樹。部分內容參考網絡資源

用決策樹(CART)解決iris分類問題

datasets oba 可能 rom art PE 子集 花卉 調用 首先先看Iris數據集 Sepal.Length——花萼長度 Sepal.Width——花萼寬度 Petal.Length——花瓣長度 Petal.Width——花瓣寬度 通過上述4中屬性可以預測花卉屬

ID3決策樹中連續值的處理+周志華《機器學習》圖4.8和圖4.10繪製

轉載自 https://blog.csdn.net/Leafage_M/article/details/80137305 用一句話總結這篇部落格的內容就是: 對於當前n條資料,相鄰求平均值,得到n-1個分割值,要點如下: ①連續數值特徵的熵計算就是對上面的n-1個分割值不停嘗試, 嘗試得

西瓜書決策樹ID3演算法實現，離散屬性

from math import log import operator import csv def readDataset(filename): ''' 讀取資料 :param filename: 資料檔名，CSV格式 :return: 以列表形式返回資料列

決策樹的使用及資料視覺化

from sklearn import tree dtr=tree.DecisionTreeRegressor(max_depth=2)#例項化一個決策樹類 dtr.fit(housing.data[:,[6,7]],housing.target)#呼叫fit函式進行訓練 dot_data=

決策樹（三）剪枝

    可以這樣理解，剪枝後剩下的計算損失函式比剪枝前更小。   來源： https://blog.csdn.net/bird_fly_i/article/details/72824639?utm_sourc

決策樹-CART迴歸樹

1、什麼是CART？ CART，又名分類迴歸樹，是在ID3的基礎上進行優化的決策樹，學習CART記住以下幾個關鍵點： （1）CART既能是分類樹，又能是分類樹； （2）當CART是分類樹時，採用GINI值作為節點分裂的依據；當CART是迴歸樹時，採用樣本的最小方差作為節

決策樹三大演算法之一ID3

一、決策樹 決策樹是一種樹形結構，每一個內部節點表示在某一屬性上的測試，每一條分支代表一個測試輸出，每一個葉子節點代表一種類別。 決策樹採用的是自頂向下的遞迴方法，其基本思想是以資訊熵為度量建立一個資訊熵下降最快的樹。到葉子節點處的熵值為0，每一個葉子節點中的例

決策樹ID3演算法和C4.5演算法實戰

老師給的題目： 程式碼實現【兩種演算法合在一個檔案裡】：  from numpy import * def createDataSet(): dataSet = [[1, 1, 1, 0, 'no'], [1, 1, 1, 1, '

《機器學習實戰》決策樹(ID3演算法)的分析與實現

        決策樹是一個預測模型；他代表的是物件屬性與物件值之間的一種對映關係。樹中每個節點表示某個物件，而每個分叉路徑則代表的某個可能的屬性值，而每個葉結點則對應從根節點到該葉節點所經歷的路徑所表示的物件的值。決策樹僅有單一輸出，若欲有複數輸出，可以建立獨立的決策樹以處理不同輸出。 資料探勘中決策樹是一

IBM SPSS Modeler算法系列-----決策樹CHAID演算法

在之前的微信文章中，有一篇名為《SPSS Modeler決策樹演算法比較》的文章，粗略介紹了SPSS Modeler中各種決策樹演算法（包括C5.0、CHAID、QUEST、C&R和決策列表）的區別，這可以幫助大家在選用演算法的時候有一些參考。 談到演算法，大家都覺