決策樹-CART迴歸樹
1、什麼是CART？
CART，又名分類迴歸樹，是在ID3的基礎上進行優化的決策樹，學習CART記住以下幾個關鍵點：
（1）CART既能是分類樹，又能是分類樹；
（2）當CART是分類樹時，採用GINI值作為節點分裂的依據；當CART是迴歸樹時，採用樣本的最小方差作為節點分裂的依據；
（3）CART是一棵二叉樹。
分類樹的作用是通過一個物件的特徵來預測該物件所屬的類別，而回歸樹的目的是根據一個物件的資訊預測該物件的屬性，並以數值表示。
CART既能是分類樹，又能是決策樹，如上表所示，如果我們想預測一個人是否已婚，那麼構建的CART將是分類樹；如果想預測一個人的年齡，那麼構建的將是迴歸樹。
2、CART如何選擇分裂的屬性？
分裂的目的是為了能夠讓資料變純，使決策樹輸出的結果更接近真實值。那麼CART是如何評價節點的純度呢？如果是分類樹，CART採用GINI值衡量節點純度；如果是迴歸樹，採用樣本方差衡量節點純度。節點越不純，節點分類或者預測的效果就越差。
GINI值的計算公式：
節點越不純，GINI值越大。以二分類為例，如果節點的所有資料只有一個類別，則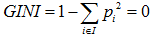
，如果兩類數量相同，則
。
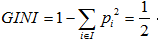迴歸方差計算公式：
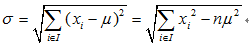
方差越大，表示該節點的資料越分散，預測的效果就越差。如果一個節點的所有資料都相同，那麼方差就為0，此時可以很肯定得認為該節點的輸出值；如果節點的資料相差很大，那麼輸出的值有很大的可能與實際值相差較大。
因此，無論是分類樹還是迴歸樹，CART都要選擇使子節點的GINI值或者回歸方差最小的屬性作為分裂的方案。即最小化（分類樹）：
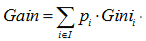
或者（迴歸樹）：
3、如何剪枝？
為防止過擬合，需要對生成的樹進行剪枝。
CART採用CCP（代價複雜度）剪枝方法。代價複雜度選擇節點表面誤差率增益值最小的非葉子節點，刪除該非葉子節點的左右子節點，若有多個非葉子節點的表面誤差率增益值相同小，則選擇非葉子節點中子節點數最多的非葉子節點進行剪枝。
CCP（代價複雜度）剪枝方法描述如下：
令決策樹的非葉子節點為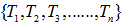
。
a）計算所有非葉子節點的表面誤差率增益值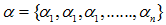
b）選擇表面誤差率增益值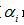
最小的非葉子節點
（若多個非葉子節點具有相同小的表面誤差率增益值，選擇節點數最多的非葉子節點）。
c）對
進行剪枝
表面誤差率增益值的計算公式：
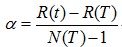
其中：
表示葉子節點的誤差代價，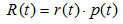
，
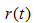為節點的錯誤率， 
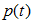為節點資料量的佔比；
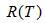表示子樹的誤差代價，
， 
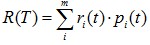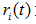為子節點i的錯誤率，
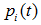表示節點i的資料節點佔比；
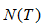表示子樹節點個數。
算例：
下圖是其中一顆子樹，設決策樹的總資料量為40。
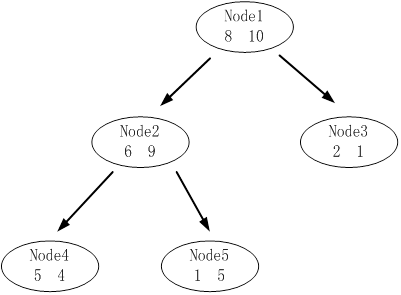
該子樹的表面誤差率增益值可以計算如下：
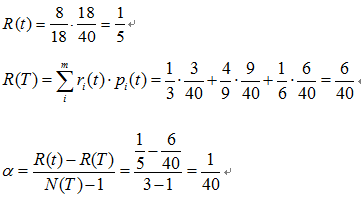
求出該子樹的表面錯誤覆蓋率為 ，只要求出其他子樹的表面誤差率增益值就可以對決策樹進行剪枝。
4、例子講解
接下來將以一個實際的例子對CART進行介紹：
表1 原始資料表
|
看電視時間 |
婚姻情況 |
職業 |
年齡 |
|
3 |
未婚 |
學生 |
12 |
|
4 |
未婚 |
學生 |
18 |
|
2 |
已婚 |
老師 |
26 |
|
5 |
已婚 |
上班族 |
47 |
|
2.5 |
已婚 |
上班族 |
36 |
|
3.5 |
未婚 |
老師 |
29 |
|
4 |
已婚 |
學生 |
21 |
分類樹和迴歸樹是怎麼做決策的？假設我們構建了兩棵決策樹分別預測使用者是否已婚和實際的年齡，如圖1和圖2所示：
圖1 預測婚姻情況決策樹 圖2 預測年齡的決策樹
圖1表示一棵分類樹，其葉子節點的輸出結果為一個實際的類別，在這個例子裡是婚姻的情況（已婚或者未婚），選擇葉子節點中數量佔比最大的類別作為輸出的類別；
圖2是一棵迴歸樹，預測使用者的實際年齡，是一個具體的輸出值。怎樣得到這個輸出值？一般情況下選擇使用中值、平均值或者眾數進行表示，圖2使用節點年齡資料的平均值作為輸出值。
CART如何分裂成一棵二叉樹？
節點的分裂分為兩種情況，連續型的資料和離散型的資料。
CART對連續型屬性的處理與C4.5差不多，通過最小化分裂後的GINI值或者樣本方差尋找最優分割點，將節點一分為二，在這裡不再敘述，詳細請看C4.5。
對於離散型屬性，理論上有多少個離散值就應該分裂成多少個節點。但CART是一棵二叉樹，每一次分裂只會產生兩個節點，怎麼辦呢？很簡單，只要將其中一個離散值獨立作為一個節點，其他的離散值生成另外一個節點即可。這種分裂方案有多少個離散值就有多少種劃分的方法，舉一個簡單的例子：如果某離散屬性一個有三個離散值X，Y，Z，則該屬性的分裂方法有{X}、{Y，Z}，{Y}、{X，Z}，{Z}、{X，Y}，分別計算每種劃分方法的基尼值或者樣本方差確定最優的方法。
以屬性“職業”為例，一共有三個離散值，“學生”、“老師”、“上班族”。該屬性有三種劃分的方案，分別為{“學生”}、{“老師”、“上班族”}，{“老師”}、{“學生”、“上班族”}，{“上班族”}、{“學生”、“老師”}，分別計算三種劃分方案的子節點GINI值或者樣本方差，選擇最優的劃分方法，如下圖所示：
第一種劃分方法：{“學生”}、{“老師”、“上班族”}
預測是否已婚（分類）：
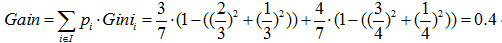
預測年齡（迴歸）：
第二種劃分方法：{“老師”}、{“學生”、“上班族”}
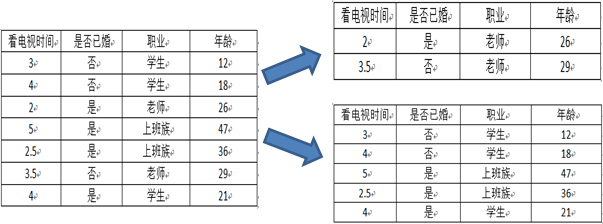
預測是否已婚（分類）：
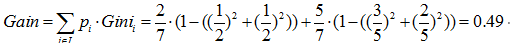
預測年齡（迴歸）：
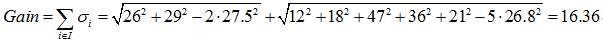
第三種劃分方法：{“上班族”}、{“學生”、“老師”}
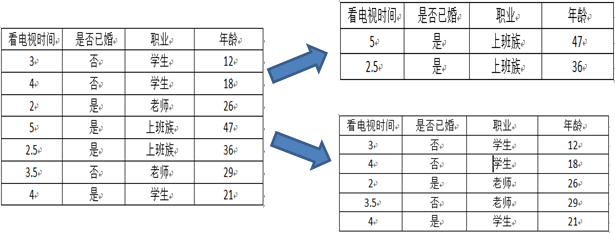
預測是否已婚（分類）：
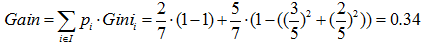
預測年齡（迴歸）：
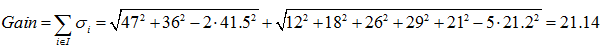
綜上，如果想預測是否已婚，則選擇{“上班族”}、{“學生”、“老師”}的劃分方法，如果想預測年齡，則選擇{“老師”}、{“學生”、“上班族”}的劃分方法。