【GLSL教程】(九)其他說明
阿新 • • 發佈:2018-11-22
法線矩陣
在很多頂點shader中都用到了gl_NormalMatrix。這裡將介紹這個矩陣是什麼,以及它的作用。
大部分計算是在檢視空間內完成的,主要原因是光照的運算要放在這個空間內,否則一些依賴觀察點座標的效果,比如鏡面反射光就很難實現。
所以我們需要將法線變換到檢視空間。變換一個頂點到檢視空間的方法如下:
下面的程式碼很簡單地實現了這個要求:
讓我們看看潛在的問題:
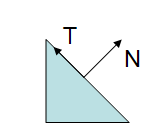
在上圖中我們可以看到一個三角面以及它的法線和切線。下圖顯示瞭如果模型檢視矩陣包含非一致縮放(non-uniform scale)的話會發生什麼。
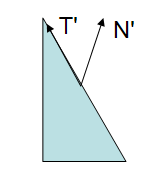
注意,如果縮放是一致的(uniform),那麼法線方向保持不變,變的只是長度,而且可以通過歸一化修正這個影響。
在上圖中,模型檢視矩陣應用到所有頂點以及法線上,最後的結果明顯錯誤:法線不再與三角面垂直了。
現在我們知道模型檢視矩陣在某些情況下,不能用來變換法線向量。下面的問題就是:那麼該使用哪個矩陣?
考慮一個3×3矩陣G,讓我們看看要正確變換法線,這個矩陣該是什麼樣子。
我們知道,變換前切線和法線是垂直的,即T•N = 0,在變換後切線和法線同樣應該保持垂直,即T’•N’ = 0。現在假設G是正確變換法線的矩陣,同時模型檢視矩陣的左上3×3子矩陣M可以正確變換切線T(T是一個向量,所以w成分為0)。因為T可以通過兩個頂點的差來計算,所以變換頂點的矩陣同樣可以用來變換T。由此可以得到如下等式:

向量的點乘相當於向量的內積,所以有:
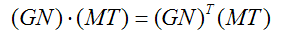
我們知道相乘的轉置等於分別轉置再交換順序相乘:
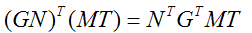
已知N和T點乘結果為0,所以如果下式成立就可以滿足等式為0:
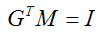
即有:

可見變換法線的正確矩陣是M的逆的轉置。OpenGL計算出的這個矩陣就儲存在gl_NormalMatrix裡。
在本節開始討論過,某些情況下使用模型檢視矩陣也可以。當模型檢視矩陣的左上3×3子矩陣M正交時,可以得到:
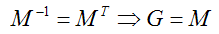
一個正交矩陣的所有行/列都為單位向量,並且互相正交。當兩個向量乘上正交矩陣時,它們之間的夾角在變換前後不變。由於這種保角變換的關係,所以法線和切線依然儲存垂直。此外,向量的長度也保持不變。
M在什麼時候能確定為正交的呢?當我們把幾何變換限制為旋轉和平移時(在OpenGL應用程式中只使用glRotate和glTranslate,而不使用glScale),就可以保證M正交。注意:gluLookAt同樣建立正交矩陣。
關於法線歸一化
當一個法線到達頂點shader後,我們一般會將它歸一化:
我們可以避免歸一化計算嗎?在某些情況下是可行的。如果gl_NormalMatrix是正交矩陣,那麼經過變換後輸入法線的長度不會變,依然等於gl_Normal。所以如果在OpenGL程式中法線已經是歸一化的,那麼在shader中就不需要在重複了。
也就是說,如果我們使用gluLookAt設定照相機,對模型值進行旋轉和平移變換,就可以在shader中避免使用歸一化操作。這對於歸一化過的光線向量也是適用的。
片斷shader的情況
在片斷shader中,我們經常發現需要重新歸一化在頂點shader中歸一化的法線。這是必要的嗎?答案是肯定的。
考慮一個包含三個不同頂點法線的三角面。片斷shader接收經過插值的法線,插值基於距離三個頂點的遠近。這樣得到的法線方向是對的,但不再是單位長度了。
下圖顯示了原因。圖中黑線表示三角面,頂點法線用藍色表示,插值得到的片斷法線用綠色表示。所有的插值法線排列在黑色的點劃線上。從圖上可以看出綠色的插值法線大小小於單位長度的頂點法線。

注意,如果頂點法線沒有單位化,那麼得到的插值法線的方向也將是錯誤的。所以,即使一個頂點沒有在頂點shader用到,也可能要對它在頂點shader中進行歸一化。
有一種情況,在片斷shader中可以避免歸一化操作,那就是每個頂點法線方向相同,而且頂點法線是經過歸一化的。此時頂點法線插值得到的結果都相同。
以方向光為例,每個片斷都需要考慮光線方向,如果光線向量已經在之前歸一化了,在片斷shader中就可以避免歸一化這一步。
在很多頂點shader中都用到了gl_NormalMatrix。這裡將介紹這個矩陣是什麼,以及它的作用。
大部分計算是在檢視空間內完成的,主要原因是光照的運算要放在這個空間內,否則一些依賴觀察點座標的效果,比如鏡面反射光就很難實現。
所以我們需要將法線變換到檢視空間。變換一個頂點到檢視空間的方法如下:
vertexEyeSpace = gl_ModelViewMatrix * gl_Vertex;下面的程式碼很簡單地實現了這個要求:
normalEyeSpace = vec3(gl_ModelViewMatrix * vec4(gl_Normal,0.0));讓我們看看潛在的問題:

在上圖中我們可以看到一個三角面以及它的法線和切線。下圖顯示瞭如果模型檢視矩陣包含非一致縮放(non-uniform scale)的話會發生什麼。

注意,如果縮放是一致的(uniform),那麼法線方向保持不變,變的只是長度,而且可以通過歸一化修正這個影響。
在上圖中,模型檢視矩陣應用到所有頂點以及法線上,最後的結果明顯錯誤:法線不再與三角面垂直了。
現在我們知道模型檢視矩陣在某些情況下,不能用來變換法線向量。下面的問題就是:那麼該使用哪個矩陣?
考慮一個3×3矩陣G,讓我們看看要正確變換法線,這個矩陣該是什麼樣子。
我們知道,變換前切線和法線是垂直的,即T•N = 0,在變換後切線和法線同樣應該保持垂直,即T’•N’ = 0。現在假設G是正確變換法線的矩陣,同時模型檢視矩陣的左上3×3子矩陣M可以正確變換切線T(T是一個向量,所以w成分為0)。因為T可以通過兩個頂點的差來計算,所以變換頂點的矩陣同樣可以用來變換T。由此可以得到如下等式:

向量的點乘相當於向量的內積,所以有:
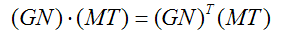
我們知道相乘的轉置等於分別轉置再交換順序相乘:
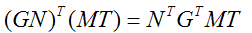
已知N和T點乘結果為0,所以如果下式成立就可以滿足等式為0:
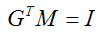
即有:

可見變換法線的正確矩陣是M的逆的轉置。OpenGL計算出的這個矩陣就儲存在gl_NormalMatrix裡。
在本節開始討論過,某些情況下使用模型檢視矩陣也可以。當模型檢視矩陣的左上3×3子矩陣M正交時,可以得到:
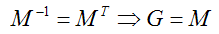
一個正交矩陣的所有行/列都為單位向量,並且互相正交。當兩個向量乘上正交矩陣時,它們之間的夾角在變換前後不變。由於這種保角變換的關係,所以法線和切線依然儲存垂直。此外,向量的長度也保持不變。
M在什麼時候能確定為正交的呢?當我們把幾何變換限制為旋轉和平移時(在OpenGL應用程式中只使用glRotate和glTranslate,而不使用glScale),就可以保證M正交。注意:gluLookAt同樣建立正交矩陣。
關於法線歸一化
當一個法線到達頂點shader後,我們一般會將它歸一化:
normal = normalize(gl_NormalMatrix * gl_Normal);我們可以避免歸一化計算嗎?在某些情況下是可行的。如果gl_NormalMatrix是正交矩陣,那麼經過變換後輸入法線的長度不會變,依然等於gl_Normal。所以如果在OpenGL程式中法線已經是歸一化的,那麼在shader中就不需要在重複了。
也就是說,如果我們使用gluLookAt設定照相機,對模型值進行旋轉和平移變換,就可以在shader中避免使用歸一化操作。這對於歸一化過的光線向量也是適用的。
片斷shader的情況
在片斷shader中,我們經常發現需要重新歸一化在頂點shader中歸一化的法線。這是必要的嗎?答案是肯定的。
考慮一個包含三個不同頂點法線的三角面。片斷shader接收經過插值的法線,插值基於距離三個頂點的遠近。這樣得到的法線方向是對的,但不再是單位長度了。
下圖顯示了原因。圖中黑線表示三角面,頂點法線用藍色表示,插值得到的片斷法線用綠色表示。所有的插值法線排列在黑色的點劃線上。從圖上可以看出綠色的插值法線大小小於單位長度的頂點法線。

注意,如果頂點法線沒有單位化,那麼得到的插值法線的方向也將是錯誤的。所以,即使一個頂點沒有在頂點shader用到,也可能要對它在頂點shader中進行歸一化。
有一種情況,在片斷shader中可以避免歸一化操作,那就是每個頂點法線方向相同,而且頂點法線是經過歸一化的。此時頂點法線插值得到的結果都相同。
以方向光為例,每個片斷都需要考慮光線方向,如果光線向量已經在之前歸一化了,在片斷shader中就可以避免歸一化這一步。
