【 Notes 】ML ALGORITHMS of TOA
ML方法是NLS方法的一個推廣版本,具體接著看:
Assuming that the error distribution is known, the ML approach maximizes the PDFs of TOA measurements to obtain the source location. When the disturbances in the measurements are zero - mean Gaussian distributed, it is shown in the following that maximization of Equations 1 will correspond to a weighted version of the NLS scheme.
第 個
的PDF:

向量形式:
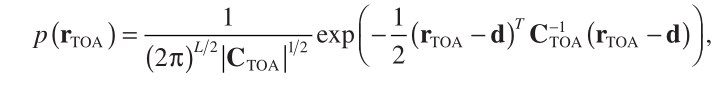 (1)
(1)
the covariance matrix for


![]()
To facilitate the maximization of Equation (1) , we consider its logarithmic version:
 (2)
(2)
As the first term is independent of x , maximizing Equation (2) is in fact equivalent to minimizing the second term, the ML estimate is
 (3)
(3)
or we can write
 (4)
(4)
where denotes the ML cost function for TOA - based positioning, which has the form of
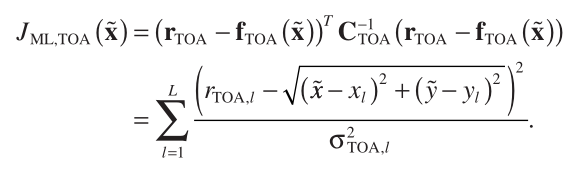 (5)
(5)
Comparing Equations (4) and (5) , it is observed that in the presence of zero - mean Gaussian noise, the ML estimator generalizes the NLS method because the former is a weighted version of the latter.
比較等式(4)和(5),觀察到在存在零均值高斯噪聲的情況下,ML估計器推廣了NLS方法,因為前者是後者的加權版本。
Intuitively speaking, when is large, which corresponds to a large noise in
, a small weight of
is employed in the squared term of

and vice versa.
When is proportional to the identity matrix or
are identical, the ML estimator is reduced to the NLS method. To compute Equation (4) , we can follow the numerical methods discussed in the NLS approach. In particular, the Newton – Raphson procedure for Equation (4) is
 (6)
(6)
 (7)
(7)
 (8)
(8)
 (9)
(9)
 (10)
(10)
 (11)
(11)
On the other hand, the corresponding Gauss – Newton and steepest descent algorithms are, respectively,
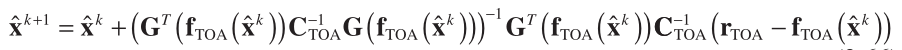 (12)
(12)
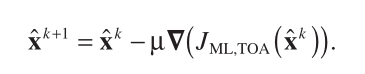 (13)
(13)
下面的博文,將對這三種方法進行TOA定位模擬。
