題目：

這門課是用魔咒將一種動物變成另一種動物。例如將貓變成老鼠的魔咒是haha，將老鼠變成魚的魔咒是hehe，把貓變成魚，魔咒lalala。反方向變化的魔咒就是簡單地將原來的魔咒倒過來念，例如ahah可以將老鼠變成貓。

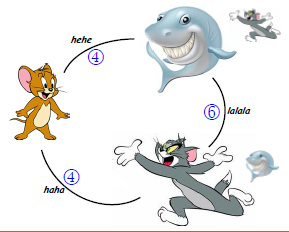
只允許帶一隻動物，考察把這隻動物變成任意一隻指定動物的本事。於是他來問你：帶什麼動物去可以讓最難變的那種動物（即該動物變為自己帶去的動物所需要的魔咒最長）需要的魔咒最短？

例如：如果只有貓、鼠、魚，則顯然哈利·波特應該帶鼠去，因為鼠變成另外兩種動物都只需要念4個字元；而如果帶貓去，則至少需要念6個字元才能把貓變成魚；同理，帶魚去也不是最好的選擇。

輸入說明：

輸出格式：
輸出哈利·波特應該帶去考場的動物的編號、以及最長的變形魔咒的長度，中間以空格分隔。
如果只帶1只動物是不可能完成所有變形要求的，則輸出0。如果有若干只動物都可以備選，則輸出編號最小的那隻。

題意理解：

利用Floyd演算法，將任意兩點之間的最小路徑計算出來。對於每一個節點，找出從該節點出發最難變的動物需要多少字元。所有節點最難變的節點的最小值即為所求結果，對應的節點為所求節點。

程式框架搭建

使用鄰接矩陣儲存圖

程式整體包括兩部分：
第一部分，建立一個圖，包括完成圖的定義，建立一個空圖，插入所有節點。
第二部分：呼叫Flody演算法，計算出任意兩頂點之間的最小距離；對於每個頂點，找出最遠的頂點距離；在每個頂點對應的最遠距離中找最小值。

完整c++程式碼

#include<iostream>
using namespace std;

#define MaxVertexNum 100	/* 最大頂點數設為100 */
#define INFINITY 65535		/* ∞設為雙位元組無符號整數的最大值65535*/
typedef int Vertex;
 
			/* 用頂點下標表示頂點,為整型*/
typedef int WeightType;		/* 邊的權值設為整型*/
//typedef char DataType;	/* 頂點儲存的資料型別設為字元型*/

/* 邊的定義*/
typedef struct ENode *PtrToENode;
struct ENode{
	Vertex V1, V2;		/* 有向邊<V1, V2> */
	WeightType Weight;	/* 權重*/
};
typedef PtrToENode Edge;

/* 圖結點的定義*/
typedef struct GNode *PtrToGNode;
struct GNode{
	int Nv;	/* 頂點數*/
	int Ne;	/* 邊數*/
	WeightType G[MaxVertexNum][MaxVertexNum]; /* 鄰接矩陣*/
//	DataType Data[MaxVertexNum]; /* 存頂點的資料*/
	/* 注意：很多情況下，頂點無資料，此時Data[]可以不用出現*/
};
typedef PtrToGNode MGraph; /* 以鄰接矩陣儲存的圖型別*/

MGraph CreateGraph(int VertexNum)
{ /* 初始化一個有VertexNum個頂點但沒有邊的圖*/
	Vertex V, W;
	MGraph Graph;

	Graph = (MGraph)malloc(sizeof(struct GNode)); /* 建立圖*/
	Graph->Nv = VertexNum;
	Graph->Ne = 0;
	/* 初始化鄰接矩陣*/
	/* 注意：這裡預設頂點編號從0開始，到(Graph->Nv - 1) */
	for (V = 0; V<Graph->Nv; V++)
		for (W = 0; W<Graph->Nv; W++)
			Graph->G[V][W] = INFINITY;
	return Graph;
}

void InsertEdge(MGraph Graph, Edge E)
{
	/* 插入邊<V1, V2> */
	Graph->G[E->V1][E->V2] = E->Weight;
	/* 若是無向圖，還要插入邊<V2, V1> */
	Graph->G[E->V2][E->V1] = E->Weight;
}

MGraph BuildGraph()
{
	MGraph Graph;
	Edge E;
//	Vertex V;
	int Nv, i;

	cin>>Nv;					/* 讀入頂點個數*/
	Graph = CreateGraph(Nv);	/* 初始化有Nv個頂點但沒有邊的圖*/

	cin>>(Graph->Ne);			/* 讀入邊數*/
	if (Graph->Ne != 0)			/* 如果有邊*/
	{
		E = (Edge)malloc(sizeof(struct ENode)); /* 建立邊結點*/
		/* 讀入邊，格式為"起點終點權重"，插入鄰接矩陣*/
		for (i = 0; i<Graph->Ne; i++)
		{
			cin>>(E->V1)>>(E->V2)>>(E->Weight);
			/* 注意：如果權重不是整型，Weight的讀入格式要改*/
			E->V1--; E->V2--; //起始編號從0開始
			InsertEdge(Graph, E);
		}
	}
	/* 如果頂點有資料的話，讀入資料
	for (V = 0; V<Graph->Nv; V++)
		scanf(" %c", &(Graph->Data[V]));
	*/
	return Graph;
}

void Floyd(MGraph Graph, WeightType D[][MaxVertexNum])
{
	Vertex i, j, k;
	/* 初始化*/
	for (i = 0; i < Graph->Nv; i++)
		for (j = 0; j < Graph->Nv; j++)
		{
			D[i][j] = Graph->G[i][j];
		}

	for (k = 0; k < Graph->Nv; k++)
		for (i = 0; i < Graph->Nv; i++)
			for (j = 0; j < Graph->Nv; j++)
				if (D[i][k] + D[k][j] < D[i][j])
				{
					D[i][j] = D[i][k] + D[k][j];
					if (i == j && D[i][j] < 0) /* 若發現負值圈*/
						return; /* 不能正確解決，返回錯誤標記*/
				}
}

WeightType FindMaxDist(WeightType D[][MaxVertexNum],
	Vertex i, int N)
{
	WeightType MaxDist;
	Vertex j;
	MaxDist = 0;
	for (j = 0; j<N; j++) /* 找出i到其他動物j的最長距離*/
		if (i != j && D[i][j]>MaxDist)
			MaxDist = D[i][j];
	return MaxDist;
}

void FindAnimal(MGraph Graph)
{
	WeightType D[MaxVertexNum][MaxVertexNum], MaxDist, MinDist;
	Vertex Animal, i;

	Floyd(Graph, D);
	
	MinDist = INFINITY;
	for (i = 0; i<Graph->Nv; i++)
	{
		MaxDist = FindMaxDist(D, i, Graph->Nv);
		if (MaxDist == INFINITY)/* 說明有從i無法變出的動物*/
		{
			cout<<0<<endl;
			return;
		}
		if (MinDist > MaxDist)	/* 找到最長距離更小的動物*/
		{
			MinDist = MaxDist;	/*更新距離*/
			Animal = i + 1;		/*記錄編號*/
		}
	}
	cout<<Animal<<" "<<MinDist<<endl;
}

int main()
{
	MGraph G = BuildGraph();
	FindAnimal(G);
	return 0;
}