哈利·波特要考試了，他需要你的幫助。這門課學的是用魔咒將一種動物變成另一種動物的本事。例如將貓變成老鼠的魔咒是haha，將老鼠變成魚的魔咒是hehe等等。反方向變化的魔咒就是簡單地將原來的魔咒倒過來念，例如ahah可以將老鼠變成貓。另外，如果想把貓變成魚，可以通過念一個直接魔咒lalala，也可以將貓變老鼠、老鼠變魚的魔咒連起來念：hahahehe。

現在哈利·波特的手裡有一本教材，裡面列出了所有的變形魔咒和能變的動物。老師允許他自己帶一隻動物去考場，要考察他把這隻動物變成任意一隻指定動物的本事。於是他來問你：帶什麼動物去可以讓最難變的那種動物（即該動物變為哈利·波特自己帶去的動物所需要的魔咒最長）需要的魔咒最短？例如：如果只有貓、鼠、魚，則顯然哈利·波特應該帶鼠去，因為鼠變成另外兩種動物都只需要念4個字元；而如果帶貓去，則至少需要念6個字元才能把貓變成魚；同理，帶魚去也不是最好的選擇。

輸入格式:

輸入說明：輸入第1行給出兩個正整數N (≤100)和M，其中N是考試涉及的動物總數，M是用於直接變形的魔咒條數。為簡單起見，我們將動物按1~N編號。隨後M行，每行給出了3個正整數，分別是兩種動物的編號、以及它們之間變形需要的魔咒的長度(≤100)，數字之間用空格分隔。

輸出格式:

輸出哈利·波特應該帶去考場的動物的編號、以及最長的變形魔咒的長度，中間以空格分隔。如果只帶1只動物是不可能完成所有變形要求的，則輸出0。如果有若干只動物都可以備選，則輸出編號最小的那隻。

輸入樣例:
6 11
3 4 70
1 2 1
5 4 50
2 6 50
5 6 60
1 3 70
4 6 60
3 6 80
5 1 100
2 4 60
5 2 80

輸出樣例:
4 70

題目看起來特別的複雜，但是確非常的簡單。
如果把動物看成圖的頂點，魔咒的長度看成是頂點之間的權重的話，那麼題目就變成了。求最短路徑問題了。及變成了求這麼一個頂點使得其到圖中任意頂點的最大路徑長度最小。是不是感覺很繞啊。。。就舉上面那個栗子吧。
根據上面的輸入，其所得到的圖為

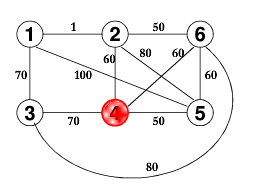
使用Floyd演算法計算出任意兩個頂點之間的最短路徑為

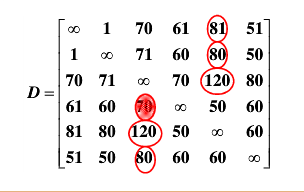
其中頂點1到剩餘頂點的最大路徑為81。為了方便我們使用dist(1)=81表示。而
dist(2)=80;dist(3)=120;dist(4)=70;dist(5)=120;dist(6)=80; 因此我們有minDist(4) = 70;

Talk is cheap, show me the code!

#include<iostream>
#include<vector>

using namespace std;

//定義一個最大值
#define MAX_LEN  10001

// 定義圖的儲存結構
// 使用鄰接矩陣來儲存圖
#define Graph vector<vector<int>>

/** \brief 建立一個使用鄰接矩陣表示的圖
 *
 * \param N : 頂點的個數
 * \param M : 邊的條數
 * \return 鄰接矩陣
 */
Graph createGraph(int N, int M)
{
    Graph graph(N, vector<int>(N, MAX_LEN)); //建立一個NxN的矩陣
    while(M--) {
        int a, b, weight;
        cin >> a >> b >> weight;
        // 注意：陣列的下標是從0開始
        graph[a-1][b-1] = weight;
        graph[b-1][a-1] = weight;
    }
    return graph;
}

/** \brief Floyd演算法，求任意兩個頂點之間的最短路徑
 * \param graph : 使用鄰接矩陣表示的圖
 * \return 最短路徑
 */
vector<vector<int>> floyd(Graph graph)
{
    Graph D(graph);     //初始化
    int N = graph.size();   //頂點的個數

    for (int k = 0; k < N; ++k) {
        for (int i = 0; i < N; ++i) {
            for (int j = 0; j < N; ++j) {
                if (k != i || i != j)  // 不計算自己到自己的長度
                    D[i][j] = min(D[i][j], D[i][k] + D[k][j]);
            }
        }
    }
    return D;
}

/** \brief 計算頂點vertex到其它頂點的最大路徑長度
 */
int findMaxDist(int vertex, vector<vector<int>> D)
{
    int maxDist = 0;
    for (int i = 0; i < D[vertex].size(); ++i)
        if (i != vertex)
            maxDist = max(maxDist, D[vertex][i]);
    return maxDist;
}

int main()
{
    int N, M;
    cin >> N >> M;
    auto graph = createGraph(N, M);
    auto D = floyd(graph);

    int animal = 0, miniDist = MAX_LEN;
    for(int i = 0; i < N; ++i) {
        auto dist = findMaxDist(i, D);
        if (dist >= MAX_LEN) {
            cout << 0 << endl;
            return 0;
        }
        if (miniDist > dist) {
            animal = i + 1;  //注意
            miniDist = dist;
        }
    }
    cout << animal << " " << miniDist << endl;

    return 0;
}