機器人的位姿描述與座標變換是進行工業機器人運動學和動力學分析的基礎。本節簡要介紹上述內容，明確位姿描述和座標變換的關係，用到的基本數學知識就是——矩陣。

1.位姿表示

位姿代表位置和姿態。任何一個剛體在空間座標系(OXYZ)中可以用位置和姿態來精確、唯一表示其位置狀態。

• 位置：x、y、z座標
• 姿態：剛體與OX軸的夾角rx、與OY軸的夾角ry、與OZ軸的夾角rz

假設基座標系為OXYZ，剛體座標系為O`X`Y`Z`。對於機器人而言，空間中的任何一個點都必須要用上述六個引數明確指定，即(x,y,z,rx,ry,rz)，即便(x,y,z)都一樣，(rx,ry,rz)不同代表機器人以不同的姿態去到達同一個點。

剛體的位置可以用一個3x1的矩陣來表示，即剛體座標系中心O`在基座標系中的位置，即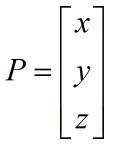

剛體的姿態可以用一個3x3的矩陣來表示，即剛體座標系在基座標系中的姿態，即

其中，第一列表示剛體座標系的O`X`軸在基座標系的三個軸方向上的分量，稱為單位主向量。同理，第二列和第三列分別是剛體座標系的O`Y`軸和O`Z`軸在基座標系的三個軸方向上的分量。

舉個例子，在下圖中，剛體M沿座標系O中平移了（0,20,15），繞Z軸旋轉了90度，因此剛體M在座標系O的位姿可描述為：

，

根據上面的例子，很容易得到，剛體座標系繞X軸（Y軸、Z軸）旋轉角度θ後的姿態矩陣為：

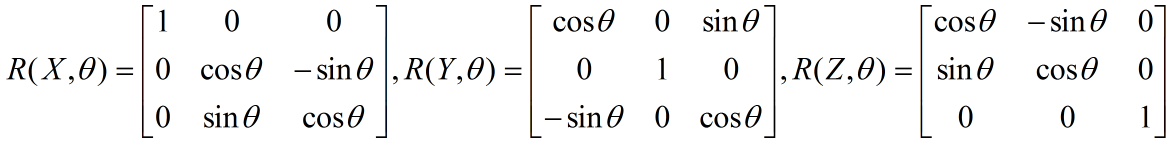
2.齊次座標與齊次矩陣

2.1 齊次座標

其中，x=a/w, y=b/w, z=c/w 。

• 點的齊次座標

對於某一個點(10,20,30)，它的齊次座標可以表示為

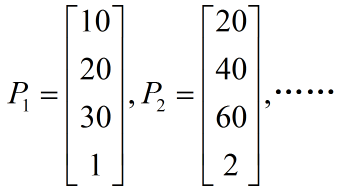
• 座標軸的齊次座標

2.2 齊次矩陣

機器人學中，用齊次矩陣（4x4）來統一描述剛體的位置和姿態，如下圖。通過矩陣的正逆變換和矩陣相乘操作，實現位姿的變換。

其中，前面的3x3矩陣代表剛體的姿態，後面的3x1矩陣代表剛體的位置。

2.3 齊次變換

有了上述基礎，接下來可以用齊次變換來描述剛體在空間中的位姿變換了。齊次矩陣不僅可以描述剛體在空間中的位姿，還可以描述位姿變換過程，比如“繞某某座標系的X軸旋轉43°，並且繞Y軸旋轉-89°”。齊次變換分為平移變換、旋轉變換以及前兩者的結合。

2.3.1 平移變換

平移變換較為簡單，比如座標系j相對座標系i的x、y、z分別平移10,-20,30，用齊次矩陣表示如下：

其中，矩陣位置可以交換，因為這是三個相互獨立的變數，交換後不影響結果。

2.3.2 旋轉變換

例1：座標系j相對座標系i的X軸旋轉90°，齊次矩陣描述如下：

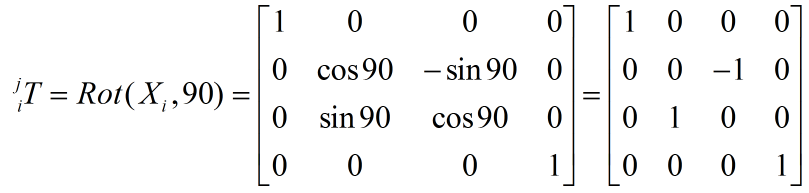
例2：座標系j相對座標系i的X軸旋轉90°，並繞座標系i的Y軸旋轉90°，由例1得到“座標系j相對座標系i的X軸旋轉90°”的變換描述，也容易得到“繞座標系i的Y軸旋轉90°”的變換描述。但是這兩個矩陣能否像平移變換一樣隨意交換次序呢？答案是否定的，矩陣左乘和矩陣右乘的意義是不一樣的：

• 變換運算元左乘：表示該變換是相對固定座標系變換
• 變換運算元右乘：表示該變換是相對動的座標系（新座標系）變換。

需要解釋的是，我們把上述的平移變換和旋轉變換稱為變換運算元。

根據上述原則，則例2中，兩個變換都是繞座標系i的變換，是繞固定座標系的變換，變換運算元應該左乘。假設剛體j原位姿的齊次矩陣描述為P，那麼經歷“座標系j相對座標系i的X軸旋轉90°”後的描述為：

即，變換運算元左乘。接下來第二個變換是“繞座標系i的Y軸旋轉90°”，也應該左乘：

例3：座標系j相對座標系i的X軸旋轉90°，並繞座標系j的Y軸旋轉90°。

這一題與例2的區別在於第二個變換改成了“繞座標系j的Y軸旋轉90°”。首先第一個變換沒啥變換，與例2的第一個變換一樣，繞固定座標系旋轉，左乘。第二個變換應該是：

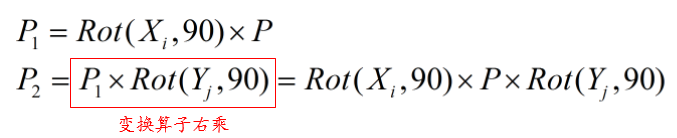
2.3.3 平移＋旋轉變換

這裡平移變換運算元可以直接加到旋轉變換運算元裡（試試就知道了，平移與旋轉是相對獨立的）。這裡既然講到平移與旋轉的綜合變換，不如說下“已知剛體i的空間位姿引數為（x,y,z,rx,ry,rz），如何用齊次矩陣來描述？”這就好比剛體座標系j與固定座標系i最開始完全重合，然後剛體j沿座標系i的X、Y、Z方向分別移動距離x，y和z，並且繞座標系i的X軸、Y軸、Z軸分別旋轉rx、ry和rz。

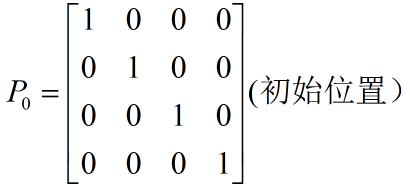
講到這裡，機器人的位姿描述與座標變換也就基本結束了。上述知識是進行機器人運動學分析、動力學分析、機器人離線程式設計軟體開發等的基礎。尤其在機器人逆運動學分析和模擬過程、工業現場手眼標定等場合，齊次矩陣的變換尤其重要。有了上述基礎，再去看Jungle之前的兩篇文章：

https://blog.csdn.net/sinat_21107433/article/details/78937391

https://blog.csdn.net/sinat_21107433/article/details/80169043