PMSM 控制技術探究與模擬1:三相PMSM的數學建模與座標變換
PMSM 控制技術探究與模擬1:三相PMSM的數學建模與座標變換
永磁同步電機(PMSM:permanent magnet synchronous motor)是一個強耦合、複雜的非線性系統,為了能夠更好地理解PMSM及其控制演算法,特此開啟這個PMSM的部落格系列。本系列基於《線代永磁同步電機控制原理及MATLAB模擬》(袁雷,北京航空航天大學出版社)以及鄙人看過的論文等資料進行編撰。下面的連結裡可以下載該書的PDF、例程模型和TI電機驅動PPT。將資料吃透有益於理解PMSM的向量控制方法。轉載本部落格請註明出處。
https://download.csdn.net/download/huagengpai1994/10811757
1,三相PMSM的基本數學模型
1.1 三相PMSM 的結構
當三相PMSM轉子磁路的結構不同時,電機的執行效能、控制方法、製造工藝和適用場合也會不同。目前,根據永磁體轉子上的位置不同,三相PMSM的轉子結構可以分為表貼式和內建式兩種結構,具體如下圖所示:

對於表貼式轉子結構而言,由於其具有結構簡單、製造成本低和轉動慣量小等優點,在恆功率執行範圍不寬的三相PMSM 和永磁無刷直流電機中得到廣泛應用。表貼式轉子結構中的永磁磁極易於實現最優設計,能使電機的氣隙磁密波形趨於正弦波分佈,進而提高電機的執行效能。內建式轉子結構可以充分利用轉子磁路不對稱所產生的磁阻轉矩,提高電機的功率密度,使得電機的動態效能較表貼式轉子結構有所玫善,製造工藝也較簡單,但漏磁係數和製造成本都較表貼式轉子結構大。對於採用稀土永磁材料的電機來說,由於永磁材料的磁導率接近1,所以表貼式轉子結構在電滋效能上屬於隱極轉子結構;而內建式轉子結構相鄰永磁磁極間有著磁導率很大的改磁材料,在電磁效能上屬於凸極轉子結構。
1.2 基本數學模型
對於三相PMSM而言,基本的可變輸入是三相交流電流,即電流向量(包括大小和角度),輸出是轉矩和轉速。在三相PMSM裡面三相電流的電角度嚴格互差120度,所以只能變動電流的大小。構建數學模型的意義在於,搞明白在被控物件的每一狀態下,輸入怎樣的電流(或電壓)會輸出怎樣的轉矩和轉速。研究清楚這個後,相當於知道了對於被控物件,在當下瞬態給一個作用後在下一個瞬態會變化成什麼樣。然後,欲使物件從此狀態到達彼狀態,就需要設計控制方法,以此來確定在每時每刻該作用什麼。總結一下就是,先構建數學模型(包括力學模型、動力學模型等),再設計控制器。
為了簡化分析,假設三相PMSM為理想電機,且滿足下列條件:
- 忽略電機鐵芯的飽和
- 不計電機中的渦流和磁滯損耗
- 電機中的電流為對稱的三相正弦波電流
這樣,自然座標系下PMSM的三相電壓方程可以寫為:
u3S、R和i3S分別為:三相繞組的相電壓、相電阻和相電流。Ψ3S為三相繞組的磁鏈變化率,磁鏈的方程為:
L3S為三相繞組的電感;ψfF3S(θe)整體表示永磁體在三相繞組中產生的磁鏈,ψf為永磁體磁鏈,F3S(θe)為與電角度相關的係數(在書中該處的說法是有問題的)。
磁鏈是導電線圈或電流回路所鏈環的磁通量。其大小為導電線圈匝數N與穿過該線圈各匝的平均磁通量φ的乘積。電機都是遵循法拉第電磁感應定律,按照電能—磁能—機械能的方法驅動。
以下為矩陣的具體表示:
其中,Lm3為定子互感;Lm3為定子漏感,Θe表示電角度。解釋一下電角度:

上圖中,u,v,w為三相繞組,2極的意思是極對數為2,也就是說有2極×3相=6塊小扇區。可以看到N從V到達下一個V對於三相電流而言走完了一個完整的週期又回到了初始狀態,但是電機並沒有轉完一整圈。換言之,如果電機完整轉完一圈,那麼對於三相電流而言不過是重複了極對數遍週期過程。所以控制上直接討論的是電角度,然後換算到機械角度。多機電機的顯而易見的:轉矩和轉速的控制更精確、轉動更平滑。缺點是多極電機的電動勢中高次諧波增加,齒槽轉矩增加,由高次諧波引起的損耗增加。
電角度=機械角度×極對數 解釋結束,繼續推導公式。
根據機電能量轉換原理,電磁轉矩Te等於磁場儲能與機械角Θm位移的偏導,因此有:
其中,pn為三相PMSM的極對數。
另外,由牛頓第二定理可得電機的機械運動方程為
可以看出電磁轉矩的方程比較複雜,為了能達到想要的轉矩,去確定三相電流值是很困難的。總而言之,如此建立的三相PMSM的數學模型是一個比較複雜且強耦合的多變數系統。必須要對模型進行解耦,降階(轉矩方程中有矩陣乘法——自變數與自變數的乘積,會導致多階)。
2,三相PMSM的座標變換
2.1 d-q軸數學模型是什麼
下述英文來自TI的官方PPT,該PPT在開頭連結裡有。動畫是我從PPT裡面扒出來做的。
Assume we have a two or three phase AC motor as shown in the bottom-left animation. By properly controlling the motor’s sinusoidal currents in real time, you can create a smoothly rotating magnetic flux pattern as shown, where the frequency of rotation corresponds to the frequency of the current sinewaves. If you then place a magnetized rotor inside the stator frame, the magnetic attraction between the rotating stator flux and the rotor magnets will cause the rotor to follow this rotation. However, the animation indicates a condition of relatively low motor loading, as indicated by the fact that the orientation of the rotor magnets and stator flux are the same. As you load down the motor, you will see that the rotor angle will start to lag the stator flux angle. This effect is plotted in the center diagram, where generated motor torque is plotted against this lag angle. When the rotor flux axis is lagging the stator flux angle by 90 degrees, this is the condition of maximum torque for a given amount of stator coil current. So depending on whether we would like clockwise or counterclockwise torque, we would like the relative angle to be either -90 or +90 degrees.(假設我們有一個兩相或三相交流電動機,如左下角動畫所示。通過適當地實時控制電機的正弦電流,可以建立如圖所示的平滑旋轉的磁通模式,其中旋轉的頻率對應於電流正弦波的頻率。如果你在定子框架內放置一個磁化的轉子,那麼在旋轉的定子磁通和轉子磁鐵之間的磁吸引力將導致轉子跟隨這個旋轉。但是,該動畫顯示電機負載相對較低的情況,如轉子磁鐵和定子磁通的方向相同的事實所示。當你把馬達裝下去的時候,你會發現轉子的角度會開始滯後於定子磁通角度。這種效應在中心圖中繪製,其中產生的電機轉矩相對於這個滯後角繪製。當轉子磁鏈軸滯後於定子磁鏈角90度時,這是給定定子線圈電流時最大轉矩的條件。因此,根據我們是順時針還是逆時針扭矩,我們希望相對角度是-90度或+90度。)

It turns out that we can’t instantaneously control the axis of the rotor magnets to be at +/- 90 degrees with respect to the angle of the stator flux. But we CAN instantaneously control the angle of the stator flux to be at +/- 90 degrees with respect to the axis of the rotor magnets. This axis is called the “d” or “direct” axis. All we need is some kind of measurement to tell us where the d-axis is at, (and consequently, what angle the rotor flux is at), and from this information, we control the currents into the motor to produce a stator flux vector which is 90 degrees with respect to it. This 90 degree axis is called the “q” or “quadrature” axis. As the motor is spinning, the d-axis is also spinning. So we need to constantly update the stator currents accordingly so as to reposition the stator flux pattern to always be offset by 90 degrees from the d-axis. This is shown in real time by the animation on the right, where the red vector represents the rotor flux on the d-axis, and the green vector represents the stator flux on the q-axis. If you want more torque, you simply increase the stator flux intensity by increasing the instantaneous stator current levels, which in effect makes the green vector longer. But you always want to keep that vector to be at 90 degrees with respect to the rotor flux vector. (結果表明,我們不能瞬時控制轉子磁鐵的軸線相對於定子磁通角為+/-90度。但我們可以瞬間控制定子磁通相對於轉子磁鐵軸線的角度為+/-90度。這個軸稱為“D”軸或“直”軸。我們只需要某種測量來告訴我們d軸在什麼位置(以及轉子磁通在什麼角度),並且根據這個資訊,我們控制進入電機的電流,以產生一個相對於它90度的定子磁通向量。這個90度軸稱為“q”或“正交”軸。當電機旋轉時,D軸也在旋轉。因此,我們需要不斷地更新定子電流,以便重新定位定子磁通模式,使其總是偏離d軸90度。這在右邊的動畫中實時顯示,其中紅色矢量表示d軸上的轉子磁通,綠色矢量表示q軸上的定子磁通。如果你想要更多的轉矩,你只要通過增加瞬時定子電流水平來增加定子磁鏈強度,這實際上使綠色向量變長。但是你總是想保持這個向量相對於轉子磁通向量在90度。)
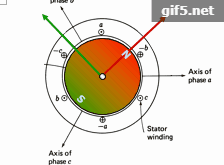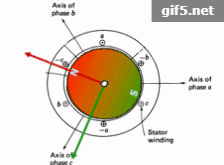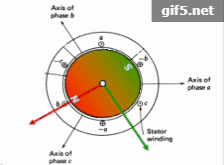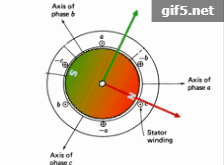
簡單來說就是:通過控制三相電流可以讓定子繞組產生旋轉的磁場,該旋轉磁場致使固定了永磁體的轉子產生相對轉動。且轉子磁鐵的軸線相對定子磁通的角度為90度(正負不同會使轉矩方向不同)時,磁場產生的轉動效果最好(簡單理解為正交時轉矩最大)。那麼我們就可以監測轉子磁鐵的軸線角度並且實時改變定子磁通的角度和大小,以達到控制轉子的目的。稱轉子磁鐵的軸線方向為“d”軸或“直軸”(紅色),實時控制改變的定子磁通向量為“q”軸或“交軸”(綠色)。d-q 正交軸是與電機轉子隨動的,向量控制或者叫場定向控制(Field Oriented Control)就是這麼來的。值得注意的一個細節是,d-q軸是在電角度意義上說的。也就是說對於多極電機,轉子完全旋轉一圈,d-q軸會旋轉多圈,並不只是圖示的這一種情況。
從這個思路出發構造出來的數學模型叫d-q軸兩相旋轉座標模型,簡稱d-q模型。
電壓方程為:
定子磁鏈方程為:
兩方程組合後電壓方程重寫為:
其中:ud、uq分別是定子電壓的d-q軸分量;id、iq分別是定子電流的d-q軸分量;R是定子電阻;ψd、ψq為定子磁鏈的d-q軸分量;ωe是電角速度;Ld、Lq分別是d-q軸電感分量;ψf代表永磁體磁鏈。
電磁轉矩方程可以寫為:
上面的四組方程是針對內建式三相PMSM建立的數學模型;對於標貼式三相PMSM,定子電感滿足Ld=Lq=Ls。因此表貼式三相PMSM的數學模型相對簡單一些。
另外,還會經常用到這幾個重要的關係式:
其中:ωm為電機的機械角速度,rad/s。Nr為電機的轉速,r/min。
現在來看整個數學模型“順”了很多,後面向量控制中若用id=0的方式,那麼轉矩就只和iq相關,電壓方程也簡化了很多。定子電壓方程有兩個,等於自變數的個數且自變數不相關,整體上這個d-q模型實現了完全的解耦。這樣欲使達到某一個轉矩(轉速與轉矩相關,位置與轉速相關,所以內環是控轉矩),就知道需要怎樣的iq和id。但是為得到想要的iq和id又該怎麼樣去輸入三相電流呢,還有d-q軸的電感如何去合成呢,這就需要座標變換來完成了。
2.2座標變換——克拉克變換與帕克變換
在電角度的平面裡面,A,B,C代表三相交流電的向量。因為規定了三相交流電互差120度所以A,B,C的方向是固定的,只有大小可以變化。α與β是固定的正交軸(相當於規範的x,y軸,我也不知道為啥這裡要用αβ),其中α與A方向重合。d-q軸就是前文中說到的隨電機旋轉的直軸與交軸。
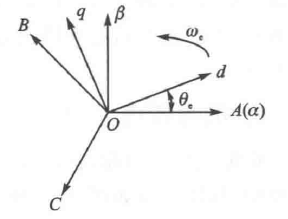
我們的目的是通過改變A,B,C三個向量的大小,然後對映到d-q軸上形成想要的d-q軸向量。但是d-q軸是隨時在變化的,而且直接轉換,計算起來不太容易,所以我們分兩步進行。
第一步:將A,B,C對映到標準正交軸α與β上 ———— 克拉克變換。
第二步:將α與β軸上的向量對映到d-q軸 ——— 帕克變換。
(說實在的,憑這倆3×3的簡單矩陣就可以在無數工程人心中留下大名,克拉克和帕克真是賺到了。“一個人的命運,當然要靠自我奮鬥,但也要考慮到歷史的程序。”)
克拉克變換如下:
其中:f代表電壓、電流或磁鏈等變數;T3s/2s為座標變換矩陣,表示為
MATLAB的simulink裡面是這個樣子的:

變換矩陣前的係數為2/3,是根據幅值不變作為約束條件得到的,即依據相電壓峰值;當採用功率不變作為約束條件時,該係數變為根號下的2/3,即依據相電壓有效值(原諒我在html中不會打根號,知道的大神評論一下)。
反過來就是反克拉克變換了,也就是矩陣求逆。
同樣的可以得到帕克變換的公式如下:
將兩個變換合起來就得到了從三相到d-q軸的變換方法,其係數矩陣如下。
反變換的係數矩陣如下:
至此,PMSM控制技術的第一篇就結束了。鄙人制作真的很辛苦啊,畢竟第一篇,要開個好頭。要是有路過的大神,請指出不足之處啊。

