2. 程式人生 > >GB、GBDT、XGboost理解

GB、GBDT、XGboost理解

阿新 • • 發佈：2018-11-23

　GBDT和xgboost在競賽和工業界使用都非常頻繁，能有效的應用到分類、迴歸、排序問題，雖然使用起來不難，但是要能完整的理解還是有一點麻煩的。本文嘗試一步一步梳理GB、GBDT、xgboost，它們之間有非常緊密的聯絡，GBDT是以決策樹（CART）為基學習器的GB演算法，xgboost擴充套件和改進了GDBT，xgboost演算法更快，準確率也相對高一些。    

1. Gradient boosting(GB)

      機器學習中的學習演算法的目標是為了優化或者說最小化loss Function， Gradient boosting的思想是迭代生多個（M個）弱的模型，然後將每個弱模型的預測結果相加，後面的模型Fm+1(x)基於前面學習模型的Fm(x)的效果生成的，關係如下：

1 \le m \le M     F_{m+1}(x) = F_m(x) + h(x)

      GB演算法的思想很簡單，關鍵是怎麼生成h(x)?

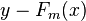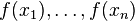      如果目標函式是迴歸問題的均方誤差，很容易想到最理想的h(x)應該是能夠完全擬合y - F_m(x) ，這就是常說基於殘差的學習。殘差學習在迴歸問題中可以很好的使用，但是為了一般性（分類，排序問題），實際中往往是基於loss Function 在函式空間的的負梯度學習，對於迴歸問題\frac{1}{2}(y - F(x))^2殘差和負梯度也是相同的。L(y, f)中的f，不要理解為傳統意義上的函式，而是一個函式向量\! f(x_1), \ldots, f(x_n)，向量中元素的個數與訓練樣本的個數相同，因此基於Loss Function函式空間的負梯度的學習也稱為“偽殘差”。

GB演算法的步驟：

　　1.初始化模型為常數值：

　　　　F_0(x) = \underset{\gamma}{\arg\min} \sum_{i=1}^n L(y_i, \gamma).

　　2.迭代生成M個基學習器

　　　　1.計算偽殘差

　　　　　　r_{im} = -\left[\frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}\right]_{F(x)=F_{m-1}(x)} \quad \mbox{for } i=1,\ldots,n.

　　　　2.基於\{(x_i, r_{im})\}_{i=1}^n生成基學習器\! h_m(x)

　　　　3.計算最優的\! \gamma_m

　　　　　　\gamma_m = \underset{\gamma}{\operatorname{arg\,min}} \sum_{i=1}^n L\left(y_i, F_{m-1}(x_i) + \gamma h_m(x_i)\right).

      　　4.更新模型

　　　　　　F_m(x) = F_{m-1}(x) + \gamma_m h_m(x).

 2. Gradient boosting Decision Tree(GBDT)

　　GB演算法中最典型的基學習器是決策樹，尤其是CART，正如名字的含義，GBDT是GB和DT的結合。要注意的是這裡的決策樹是迴歸樹，GBDT中的決策樹是個弱模型，深度較小一般不會超過5，葉子節點的數量也不會超過10，對於生成的每棵決策樹乘上比較小的縮減係數（學習率<0.1），有些GBDT的實現加入了隨機抽樣（subsample 0.5<=f <=0.8）提高模型的泛化能力。通過交叉驗證的方法選擇最優的引數。因此GBDT實際的核心問題變成怎麼基於\{(x_i, r_{im})\}_{i=1}^n

使用CART迴歸樹生成\! h_m(x)？

　　CART分類樹在很多書籍和資料中介紹比較多，但是再次強調GDBT中使用的是迴歸樹。作為對比，先說分類樹，我們知道CART是二叉樹，CART分類樹在每次分枝時，是窮舉每一個feature的每一個閾值，根據GINI係數找到使不純性降低最大的的feature以及其閥值，然後按照feature<=閾值，和feature>閾值分成的兩個分枝，每個分支包含符合分支條件的樣本。用同樣方法繼續分枝直到該分支下的所有樣本都屬於統一類別，或達到預設的終止條件，若最終葉子節點中的類別不唯一，則以多數人的類別作為該葉子節點的性別。迴歸樹總體流程也是類似，不過在每個節點（不一定是葉子節點）都會得一個預測值，以年齡為例，該預測值等於屬於這個節點的所有人年齡的平均值。分枝時窮舉每一個feature的每個閾值找最好的分割點，但衡量最好的標準不再是GINI係數，而是最小化均方差--即（每個人的年齡-預測年齡）^2 的總和 / N，或者說是每個人的預測誤差平方和 除以 N。這很好理解，被預測出錯的人數越多，錯的越離譜，均方差就越大，通過最小化均方差能夠找到最靠譜的分枝依據。分枝直到每個葉子節點上人的年齡都唯一（這太難了）或者達到預設的終止條件（如葉子個數上限），若最終葉子節點上人的年齡不唯一，則以該節點上所有人的平均年齡做為該葉子節點的預測年齡。

3. Xgboost

　　Xgboost是GB演算法的高效實現，xgboost中的基學習器除了可以是CART（gbtree）也可以是線性分類器（gblinear）。下面所有的內容來自原始paper，包括公式。

　　(1). xgboost在目標函式中顯示的加上了正則化項，基學習為CART時，正則化項與樹的葉子節點的數量T和葉子節點的值有關。

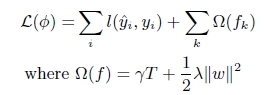
　　(2). GB中使用Loss Function對f(x)的一階導數計算出偽殘差用於學習生成fm(x)，xgboost不僅使用到了一階導數，還使用二階導數。

　　　　第t次的loss：

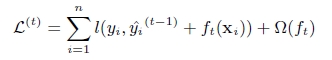
　　　　對上式做二階泰勒展開：g為一階導數，h為二階導數

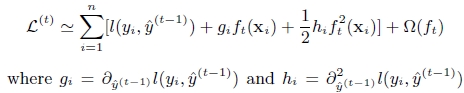
　　(3). 上面提到CART迴歸樹中尋找最佳分割點的衡量標準是最小化均方差，xgboost尋找分割點的標準是最大化，lamda，gama與正則化項相關

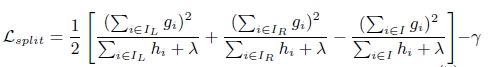
 　　xgboost演算法的步驟和GB基本相同，都是首先初始化為一個常數，gb是根據一階導數ri，xgboost是根據一階導數gi和二階導數hi，迭代生成基學習器，相加更新學習器。

xgboost與gdbt除了上述三點的不同，xgboost在實現時還做了許多優化：

  • 在尋找最佳分割點時，考慮傳統的列舉每個特徵的所有可能分割點的貪心法效率太低，xgboost實現了一種近似的演算法。大致的思想是根據百分位法列舉幾個可能成為分割點的候選者，然後從候選者中根據上面求分割點的公式計算找出最佳的分割點。
  • xgboost考慮了訓練資料為稀疏值的情況，可以為缺失值或者指定的值指定分支的預設方向，這能大大提升演算法的效率，paper提到50倍。
  • 特徵列排序後以塊的形式儲存在記憶體中，在迭代中可以重複使用；雖然boosting演算法迭代必須序列，但是在處理每個特徵列時可以做到並行。
  • 按照特徵列方式儲存能優化尋找最佳的分割點，但是當以行計算梯度資料時會導致記憶體的不連續訪問，嚴重時會導致cache miss，降低演算法效率。paper中提到，可先將資料收集到執行緒內部的buffer，然後再計算，提高演算法的效率。
  • xgboost 還考慮了當資料量比較大，記憶體不夠時怎麼有效的使用磁碟，主要是結合多執行緒、資料壓縮、分片的方法，儘可能的提高演算法的效率。

 　　參考資料：

　　1. 維基百科 Gradient boosting

　　2. XGBoost: A Scalable Tree Boosting System

　　3. 陳天奇的slides

　　4. xgboost導讀和實戰.pdf

原文來自https://www.cnblogs.com/wxquare/p/5541414.html

 

　　Boosting方法實際上是採用加法模型與前向分佈演算法。在上一篇提到的Adaboost演算法也可以用加法模型和前向分佈演算法來表示。以決策樹為基學習器的提升方法稱為提升樹（Boosting Tree）。對分類問題決策樹是CART分類樹，對迴歸問題決策樹是CART迴歸樹。

1、前向分佈演算法

　　引入加法模型

　　

　　在給定了訓練資料和損失函式L(y, f(x)) 的條件下，可以通過損失函式最小化來學習加法模型

　　

　　然而對於這個問題是個很複雜的優化問題，而且要訓練的引數非常的多，前向分佈演算法的提出就是為了解決模型的優化問題，其核心思想是因為加法模型是由多各模型相加在一起的，而且在Boosting中模型之間又是有先後順序的，因此可以在執行每一步加法的時候對模型進行優化，那麼每一步只需要學習一個模型和一個引數，通過這種方式來逐步逼近全域性最優，每一步優化的損失函式：

　　

　　具體演算法流程如下：

　　1）初始化f0(x) = 0；

　　2）第m次迭代時，極小化損失函式

　　

　　3）更新模型，則fm(x)：

　　

　　4）得到最終的加法模型

　　

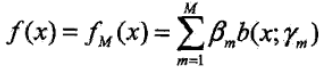
　　Adaboost演算法也可以用前向分佈演算法來描述，在這裡輸入的資料集是帶有權重分佈的資料集，損失函式是指數損失函式。

2、GBDT演算法

　　GBDT是梯度提升決策樹（Gradient Boosting Decision Tree）的簡稱，GBDT可以說是最好的機器學習演算法之一。GBDT分類和迴歸時的基學習器都是CART迴歸樹，因為是擬合殘差的。GBDT和Adaboost一樣可以用前向分佈演算法來描述，不同之處在於Adaboost演算法每次擬合基學習器時，輸入的樣本資料是不一樣的（每一輪迭代時的樣本權重不一致），因為Adaboost旨在重點關注上一輪分類錯誤的樣本，GBDT演算法在每一步迭代時是輸出的值不一樣，本輪要擬合的輸出值是之前的加法模型的預測值和真實值的差值（模型的殘差，也稱為損失）。用於一個簡單的例子來說明GBDT，假如某人的年齡為30歲，第一次用20歲去擬合，發現損失還有10歲，第二次用6歲去擬合10歲，發現損失還有4歲，第三次用3歲去擬合4歲，依次下去直到損失在我們可接受範圍內。

　　以平方誤差損失函式的迴歸問題為例，來看看以損失來擬合是個什麼樣子，採用前向分佈演算法：

　　

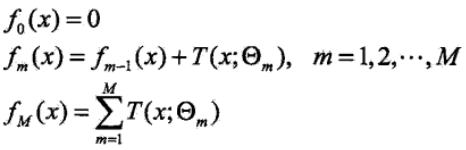
　　在第m次迭代時，我們要優化的損失函式：

　　

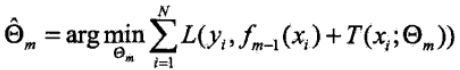
　　此時我們採用平方誤差損失函式為例：

　　

　　則上面損失函式變為：

　　

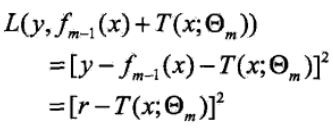
　　問題就成了對殘差r的擬合了

　　然而對於大多數損失函式，卻沒那麼容易直接獲得模型的殘差，針對該問題，大神Freidman提出了用損失函式的負梯度來擬合本輪損失的近似值，擬合一個迴歸樹

　　

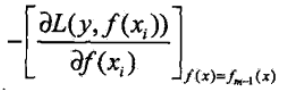
　　關於GBDT一般損失函式的具體演算法流程如下：

　　1）初始化f0(x)：

　　

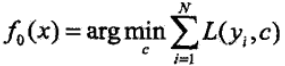
　　2）第m次迭代時，計算當前要擬合的殘差rmi：

　　　

　　以rmi為輸出值，對rmi擬合一個迴歸樹（此時只是確定了樹的結構，但是還未確定葉子節點中的輸出值），然後通過最小化當前的損失函式，並求得每個葉子節點中的輸出值cmj，j表示第j個葉子節點

　　

　　更新當前的模型fm(x)為：

　　

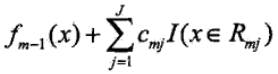
　　3）依次迭代到我們設定的基學習器的個數M，得到最終的模型，其中M表示基學習器的個數，J表示葉子節點的個數

　　

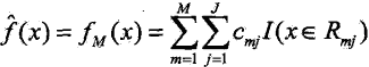
　　GBDT演算法提供了眾多的可選擇的損失函式，通過選擇不同的損失函式可以用來處理分類、迴歸問題，比如用對數似然損失函式就可以處理分類問題。大概的總結下常用的損失函式：

　　1）對於分類問題可以選用指數損失函式、對數損失函式。

　　2）對於迴歸問題可以選用均方差損失函式、絕對損失函式。

　　3）另外還有huber損失函式和分位數損失函式，也是用於迴歸問題，可以增加回歸問題的健壯性，可以減少異常點對損失函式的影響。

3、GBDT的正則化

　　在Adaboost中我們會對每個模型乘上一個弱化係數（正則化係數），減小每個模型對提升的貢獻（注意：這個係數和模型的權重不一樣，是在權重上又乘以一個0,1之間的小數），在GBDT中我們採用同樣的策略，對於每個模型乘以一個係數λ (0 < λ ≤ 1)，降低每個模型對擬合損失的貢獻，這種方法也意味著我們需要更多的基學習器。

　　第二種是每次通過按比例（推薦[0.5, 0.8] 之間）隨機抽取部分樣本來訓練模型，這種方法有點類似Bagging，可以減小方差，但同樣會增加模型的偏差，可採用交叉驗證選取，這種方式稱為子取樣。採用子取樣的GBDT有時也稱為隨機梯度提升樹（SGBT）。

　　第三種就是控制基學習器CART樹的複雜度，可以採用剪枝正則化。

4、GBDT的優缺點

　　GBDT的主要優點：

　　1）可以靈活的處理各種型別的資料

　　2）預測的準確率高

　　3）使用了一些健壯的損失函式，如huber，可以很好的處理異常值

　　GBDT的缺點：

　　1）由於基學習器之間的依賴關係，難以並行化處理，不過可以通過子取樣的SGBT來詩選部分並行。

 

5、XGBoost演算法

　　事實上對於樹模型為基學習器的整合方法在建模過程中可以分為兩個步驟：一是確定樹模型的結構，二是確定樹模型的葉子結點中的輸出值。

5.1 定義樹的複雜度

　　首先把樹拆分成結構部分q和葉子節點權重部分w，在這裡w是一個向量，表示各葉子節點中的輸出值。在這裡就囊括了上面提到的兩點，確定樹結構q和葉子結點的輸出值w。

　　

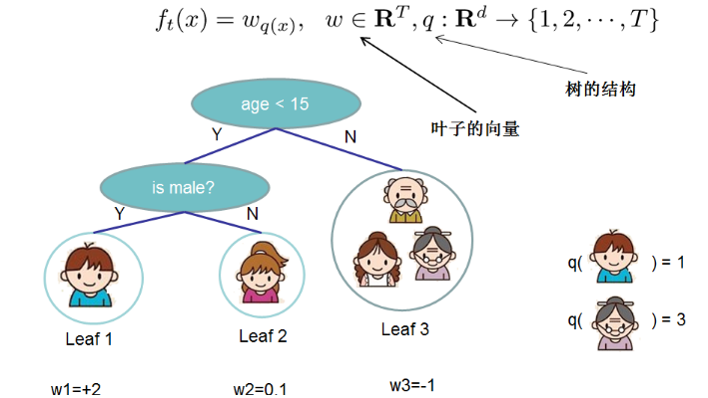
　　具體表現示例如下，引入正則化項 Ω(ft) 來控制樹的複雜度，從而實現有效的控制模型的過擬合，這是xgboost中的第一個重要點。

　　

5.2 XGBoost中的Boosting Tree模型

　　

　　和GBDT方法一樣，XGBoost的提升模型也是採用殘差，不同的是分裂結點選取的時候不一定是最小平方損失，其損失函式如下，較GBDT其根據樹模型的複雜度加入了一項正則化項：

　　

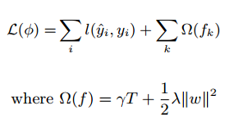
5.3 對目標函式進行改寫

　　

　　在GBDT中我們通過求損失函式的負梯度（一階導數），利用負梯度替代殘差來擬合樹模型。在XGBoost中直接用泰勒展開式將損失函式展開成二項式函式（前提是損失函式一階、二階；連續可導，而且在這裡計算一階導和二階導時可以平行計算），假設此時我們定義好了樹的結構（在後面介紹，和GBDT中直接用殘差擬合不同），假設我們的葉節點區域為：

　　

　　則我們的目標優化函式可以轉換成：

　　

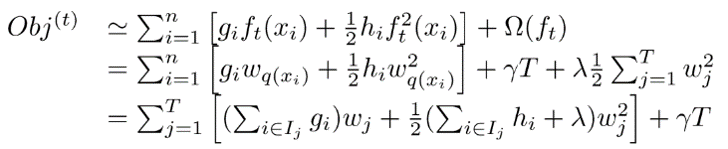
　　此時我們對wj求導並令導數為0，可得：

　　　　

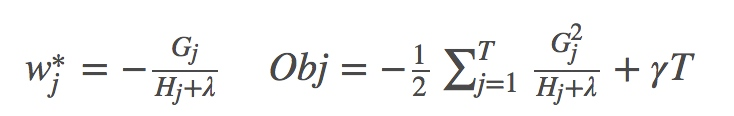
5.4 樹結構的打分函式

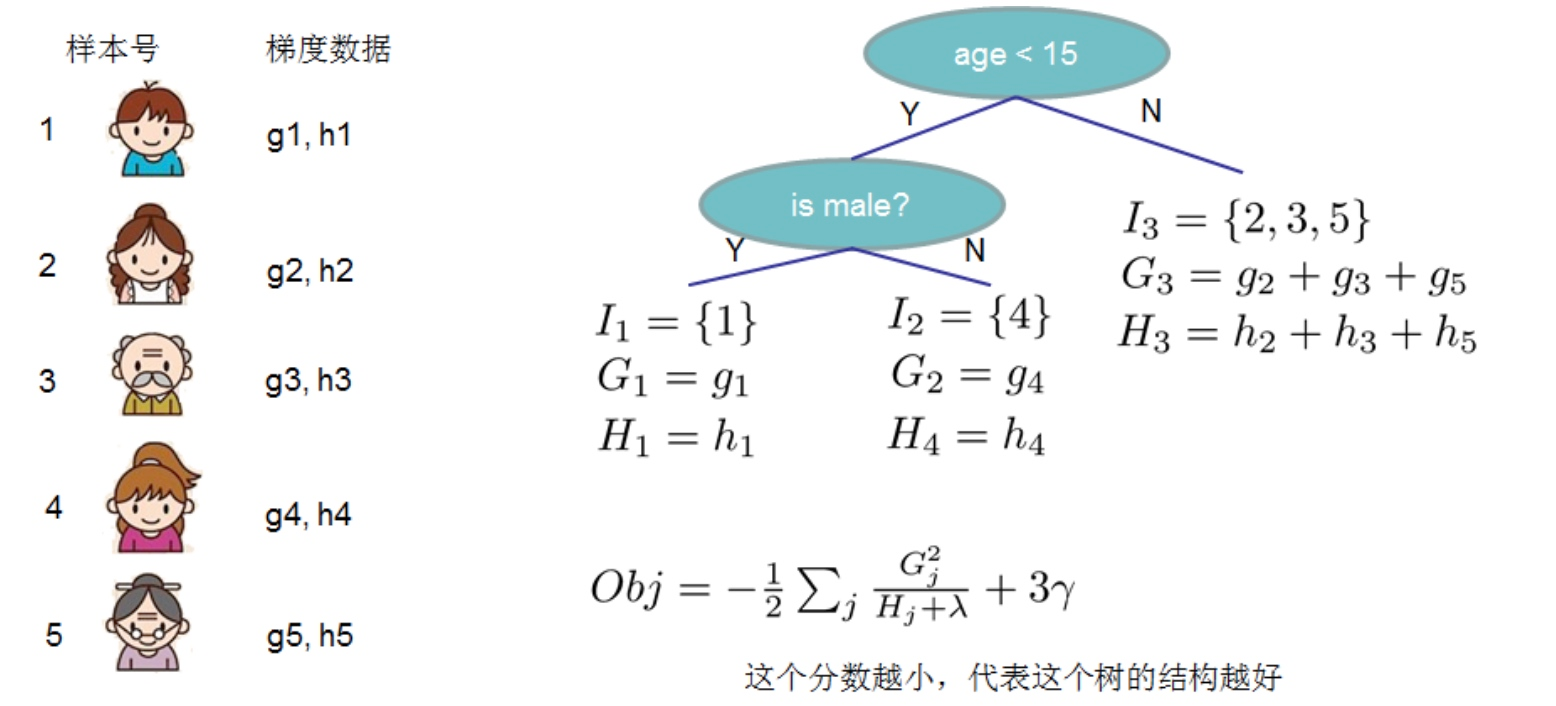
　　上面的Obj值代表當指定一個樹結構時，在目標上面最多減少多少，我們可以把它稱為結構分數。可以認為這是一個類似與基尼指數一樣更一般的對樹結構進行打分的函式。如下面的例子所示

　　

　　對於求得Obj分數最小的樹結構，我們可以列舉所有的可能性，然後對比結構分數來獲得最優的樹結構，然而這種方法計算消耗太大，更常用的是貪心法（事實上絕大多數樹模型都是這樣的，只考慮當前節點的劃分最優），每次嘗試對已經存在的葉節點（最開始的葉節點是根節點）進行分割，然後獲得分割後的增益為：

　　

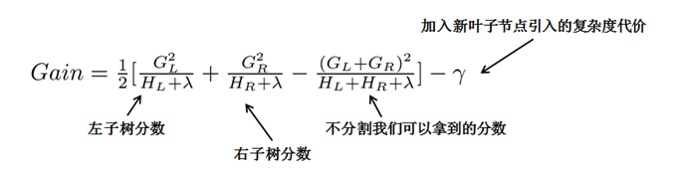
　　在這裡以Gain作為判斷是否分割的條件，如果Gain < 0，則此葉節點不做分割，然而這樣對於每次分割還是需要列出所有的分割方案（對於特徵的值的個數為n時，總共有2^n - 2 種劃分）。而實際中是採用近似貪心方法，我們先將所有樣本按照gi從小到大排序，然後進行遍歷，檢視每個節點是否需要分割（對於特徵的值的個數為n時，總共有n-1種劃分），具體示例如下：

　　

　　最簡單的樹結構就是一個節點的樹。我們可以算出這棵單節點的樹的好壞程度obj*。假設我們現在想按照年齡將這棵單節點樹進行分叉，我們需要知道：

　　1）按照年齡分是否有效，也就是是否減少了obj的值

　　2）如果可分，那麼以哪個年齡值來分。

　　此時我們就是先將年齡特徵從小到大排好序，然後再從左到右遍歷分割

　　這樣的分割方式，我們就只要對樣本掃描一遍，就可以分割出GL，GR，然後根據Gain的分數進行分割，極大地節省了時間

5.5 XGBoost中其他的正則化方法

　　1）像Adaboost和GBDT中一樣，對每一個模型乘以一個係數λ（0 < λ ≤ 1），用來降低每個模型對結果的貢獻

　　2）採用特徵子取樣方法，和RandomForest中的特徵子取樣一樣，可以降低模型的方差

6、XGBoost和GBDT的區別

　  1）將樹模型的複雜度加入到正則項中，來避免過擬合，因此泛化效能會由於GBDT

　  2）損失函式是用泰勒展開式展開的，同時用到了一階導和二階導，可以加快優化速度

　　3）和GBDT只支援CART作為基分類器之外，還支援線性分類器，在使用線性分類器的時候可以使用L1，L2正則化

　　4）引進了特徵子取樣，像RandomForest那樣，這種方法既能降低過擬合，還能減少計算

　　5）在尋找最佳分割點時，考慮到傳統的貪心演算法效率較低，實現了一種近似貪心演算法，用來加速和減小記憶體消耗，除此之外還考慮了稀疏資料集和缺失值的處理，對於特徵的值有缺失的樣本，XGBoost依然能自動找到其要分裂的方向

　　6）XGBoost支援並行處理，XGBoost的並行不是在模型上的並行，而是在特徵上的並行，將特徵列排序後以block的形式儲存在記憶體中，在後面的迭代中重複使用這個結構。這個block也使得並行化成為了可能，其次在進行節點分裂時，計算每個特徵的增益，最終選擇增益最大的那個特徵去做分割，那麼各個特徵的增益計算就可以開多執行緒進行。

 

 

原文來自：https://www.cnblogs.com/jiangxinyang/p/9248154.html

相關推薦

GB、GBDT、XGboost理解

　GBDT和xgboost在競賽和工業界使用都非常頻繁，能有效的應用到分類、迴歸、排序問題，雖然使用起來不難，但是要能完整的理解還是有一點麻煩的。本文嘗試一步一步梳理GB、GBDT、xgboost，它們之間有非常緊密的聯絡，GBDT是以決策樹（CART）為基學習器的GB演算法，xgboost擴充套件和改進了G

一步一步理解GB、GBDT、xgboost

GBDT和xgboost在競賽和工業界使用都非常頻繁，能有效的應用到分類、迴歸、排序問題，雖然使用起來不難，但是要能完整的理解還是有一點麻煩的。本文嘗試一步一步梳理GB、GBDT、xgboost，它們之間有非常緊密的聯絡，GBDT是以決策樹（CART）為基學習器的GB演算

機器學習提升演算法之Adaboost、GB、GBDT與XGBoost演算法

一、提升演算法概論 Boosting(提升)是一族可將弱學習器提升為強學習器的演算法。提升演算法基於這樣一種思想：對於一個複雜的任務，將多個專家的判斷總和得出的結果要比任何一個專家單獨的判斷好。這族演算法的工作機制類似：先從初始訓練集訓練出一個基學習器，再根據基學習器表現

整合學習之boosting，Adaboost、GBDT 和 xgboost（二）

AdaBoost 演算法的訓練誤差分析 AdaBoost最基本的性質是它能在學習過程中不斷減少訓練誤差，即在訓練資料集上的分類誤差率。 定理：AdaBoost的訓練誤差界： 1

整合學習之boosting，Adaboost、GBDT 和 xgboost（一）

在前面的部落格（https://blog.csdn.net/qq_16608563/article/details/82878127） 介紹了整合學習的bagging方法及其代表性的隨機森林。此次接著介紹整合學習的另一個方法boosting以及boosting系列的一些演算法，具體包括 Ad

整合學習之boosting，Adaboost、GBDT 和 xgboost（三）

AdaBoost演算法的解釋——前向分步法與提升樹(GBDT) 可以認為AdaBoost演算法是模型為加法模型，損失函式為指數函式、學習演算法為前向分步演算法時的二類分類學習方法。 前向分步演算法： 考慮加法模型

ml課程：決策樹、隨機森林、GBDT、XGBoost相關（含程式碼實現）

以下是我的學習筆記，以及總結，如有錯誤之處請不吝賜教。 基礎概念： 熵Entropy：是衡量純度的一個標準,表示式可以寫為： 資訊增益Information Gain：熵變化的一個量，表示式可以寫為： 資訊增益率Gain Ratio：資訊增益的變化率，表示式可以寫為：

決策樹的進化（ID3、C4.5、CART、GBDT、RF、DART、lambdaMART、XGBoost、lightGBM）

pipeline 在資料探勘領域中，決策樹是對資料進行建模的一種很有效的手段。當資料集被清洗好後，資料集就是樣本的集合，每一個樣本都是有一樣多的屬性，但屬性值可能不同（也有可能不存在即屬性值缺失）。每一個樣本，分為屬性（也可稱為特徵）和label兩部分，我們運用決策樹處理資

利用隨機森林、GBDT、xgboost、LightGBM計算準確率和auc

利用隨機森林、GBDT、xgboost、LightGBM計算準確率和auc 用到的模組 import pandas as pd import lightgbm as lgb from sklearn.model_selection import train_test_s

Boosting學習筆記（Adboost、GBDT、Xgboost）

http://www.cnblogs.com/willnote/p/6801496.html 總結得不錯 AdaBoost是最著名的Boosting族演算法。開始時，所有樣本的權重相同，訓練得到第一個基分類器。從第二輪開始，每輪開始前都先根據上一輪基分類器的分類效果調整每個樣本的權重，上一輪分錯的

RF、GBDT、XGBoost面試級整理

　　由於本文是基於面試整理，因此不會過多的關注公式和推導，如果希望詳細瞭解演算法內容，敬請期待後文。 　　 　　RF、GBDT和XGBoost都屬於整合學習（Ensemble Learning），整合學習的目的是通過結合多個基學習器的預測結果來改善單個學習器

[面試筆記] 決策樹、隨機森林、GBDT、XGBoost

摘要 本文主要分享了 決策樹、隨機森林、GBDT、XGBoost 四種模型的原理 決策樹 對於決策樹，李航老師在《統計學習方法》裡有詳細的解釋 分為ID3, C4.5, CART三個基本的樹生成演算法 ID3 是一個多叉樹，使用了熵作為

python機器學習案例系列教程——整合學習（Bagging、Boosting、隨機森林RF、AdaBoost、GBDT、xgboost）

可以通過聚集多個分類器的預測結果提高分類器的分類準確率，這一方法稱為整合（Ensemble）學習或分類器組合（Classifier Combination），該方法由訓練資料構建一組基分類器（Base Classifier），然後通過對每個基分類器的預測進行

決策樹、Bagging、隨機森林、Boosting、AdaBoost、GBDT、XGBoost

1、決策樹  一、決策樹的優點和缺點     優點： 決策樹演算法中學習簡單的決策規則建立決策樹模型的過程非常容易理解， 決策樹模型可以視覺化，非常直觀 應用範圍廣，可用於分類和迴歸，而且非常容易做多類別的分類 能夠處理數值型和連續的樣本特徵     缺點：

RF、GBDT、XGBoost、lightGBM原理與區別

　　RF、GBDT和XGBoost都屬於整合學習（Ensemble Learning），整合學習的目的是通過結合多個基學習器的預測結果來改善單個學習器的泛化能力和魯棒性。 　　根據個體學習器的生成方式，目前的整合學習方法大致分為兩大類：即個體學習器之間存在強

boosting－adaboost、GBDT、xgboost、lightGBM

提升方法，是將多個專家的判斷進行適當的綜合所得出的判斷，要比其中任何一個專家單獨的判斷好。 Kearns和Valiant提出了“強可學習”和“弱可學習”的概念 強可學習：在概率近似正確學習的框架中，一個概念（一個類），如果存在一個多項式的學習演算法能夠學習它

關於adaboost、GBDT、xgboost之間的區別與聯絡

AdaBoost:提高那些被前一輪弱分類器錯誤分類樣本的權值，而降低那些被正確分類樣本的權值。這樣一來，那些沒有得到正確分類的資料，由於其權值的加大而受到後一輪的弱分類器的更大關注，於是，分類問題就被一系列的弱分類器“分而治之”。至於第二個問題，即弱分類器的組合

GBDT、XGBoost、LightGBM演算法公式推導

一、GBDT公式推導 1、第一個基函式： (1.1)F0(X)=12log1+y‾1−y‾F_0(X)=\frac{1}{2}log\frac{1+\overline{y}}{1-\overline{y

提升方法：GBDT、XGBOOST、AdaBoost

提升 (boosting) 方法是一種常用的統計學習方法，應用廣泛且有效，在分類問題中，它通過改變訓練樣本的權重，學習多個分類器，並將這些分類器進行線性組合，提高分類器效能。 GBDT 我們知道隨機森林的決策樹分別取樣建立, 相對獨立。 那

Java、C++、Python、Ruby、PHP、C#和JavaScript的理解

皮膚 叔叔 保持 大學 學校 cti java 等等 無需 Java、C++、Python、Ruby、PHP、C#和JavaScript和日本動漫裏的那些大家熟悉的動漫人物結合起來。依據他們的身世、個人經歷來生動的表達各編程語言的發展歷程。原文內容例