一步一步理解GB、GBDT、xgboost
GBDT和xgboost在競賽和工業界使用都非常頻繁，能有效的應用到分類、迴歸、排序問題，雖然使用起來不難，但是要能完整的理解還是有一點麻煩的。本文嘗試一步一步梳理GB、GBDT、xgboost，它們之間有非常緊密的聯絡，GBDT是以決策樹（CART）為基學習器的GB演算法，xgboost擴充套件和改進了GDBT，xgboost演算法更快，準確率也相對高一些。
1. Gradient boosting(GB)
機器學習中的學習演算法的目標是為了優化或者說最小化loss Function， Gradient boosting的思想是迭代生多個（M個）弱的模型，然後將每個弱模型的預測結果相加，後面的模型Fm+1(x)基於前面學習模型的Fm(x)的效果生成的，關係如下：
GB演算法的思想很簡單，關鍵是怎麼生成h(x)?
如果目標函式是迴歸問題的均方誤差，很容易想到最理想的h(x)應該是能夠完全擬合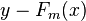
，這就是常說基於殘差的學習。殘差學習在迴歸問題中可以很好的使用，但是為了一般性（分類，排序問題），實際中往往是基於loss Function 在函式空間的的負梯度學習，對於迴歸問題
殘差和負梯度也是相同的。
中的f，不要理解為傳統意義上的函式，而是一個函式向量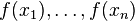
，向量中元素的個數與訓練樣本的個數相同，因此基於Loss Function函式空間的負梯度的學習也稱為“偽殘差”。
GB演算法的步驟：
1.初始化模型為常數值：
2.迭代生成M個基學習器
1.計算偽殘差
![r_{im} = -\left[\frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}\right]_{F(x)=F_{m-1}(x)} \quad \mbox{for } i=1,\ldots,n.](https://upload.wikimedia.org/math/0/b/e/0bebe45631e9a1c4ed693590d60829c0.png)
2.基於
生成基學習器
3.計算最優的
4.更新模型
2. Gradient boosting Decision Tree(GBDT)
GB演算法中最典型的基學習器是決策樹，尤其是CART，正如名字的含義，GBDT是GB和DT的結合。要注意的是這裡的決策樹是迴歸樹，GBDT中的決策樹是個弱模型，深度較小一般不會超過5，葉子節點的數量也不會超過10，對於生成的每棵決策樹乘上比較小的縮減係數（學習率<0.1），有些GBDT的實現加入了隨機抽樣（subsample 0.5<=f <=0.8）提高模型的泛化能力。通過交叉驗證的方法選擇最優的引數。因此GBDT實際的核心問題變成怎麼基於
？
CART分類樹在很多書籍和資料中介紹比較多，但是再次強調GDBT中使用的是迴歸樹。作為對比，先說分類樹，我們知道CART是二叉樹，CART分類樹在每次分枝時，是窮舉每一個feature的每一個閾值，根據GINI係數找到使不純性降低最大的的feature以及其閥值，然後按照feature<=閾值，和feature>閾值分成的兩個分枝，每個分支包含符合分支條件的樣本。用同樣方法繼續分枝直到該分支下的所有樣本都屬於統一類別，或達到預設的終止條件，若最終葉子節點中的類別不唯一，則以多數人的類別作為該葉子節點的性別。迴歸樹總體流程也是類似，不過在每個節點（不一定是葉子節點）都會得一個預測值，以年齡為例，該預測值等於屬於這個節點的所有人年齡的平均值。分枝時窮舉每一個feature的每個閾值找最好的分割點，但衡量最好的標準不再是GINI係數，而是最小化均方差--即（每個人的年齡-預測年齡）^2 的總和 / N，或者說是每個人的預測誤差平方和 除以 N。這很好理解，被預測出錯的人數越多，錯的越離譜，均方差就越大，通過最小化均方差能夠找到最靠譜的分枝依據。分枝直到每個葉子節點上人的年齡都唯一（這太難了）或者達到預設的終止條件（如葉子個數上限），若最終葉子節點上人的年齡不唯一，則以該節點上所有人的平均年齡做為該葉子節點的預測年齡。
3. Xgboost
Xgboost是GB演算法的高效實現，xgboost中的基學習器除了可以是CART（gbtree）也可以是線性分類器（gblinear）。下面所有的內容來自原始paper，包括公式。
(1). xgboost在目標函式中顯示的加上了正則化項，基學習為CART時，正則化項與樹的葉子節點的數量T和葉子節點的值有關。
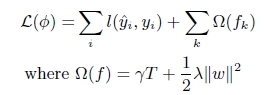
(2). GB中使用Loss Function對f(x)的一階導數計算出偽殘差用於學習生成fm(x)，xgboost不僅使用到了一階導數，還使用二階導數。
第t次的loss：
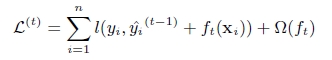
對上式做二階泰勒展開：g為一階導數，h為二階導數
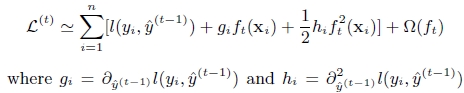
(3). 上面提到CART迴歸樹中尋找最佳分割點的衡量標準是最小化均方差，xgboost尋找分割點的標準是最大化，lamda，gama與正則化項相關
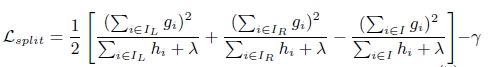
xgboost演算法的步驟和GB基本相同，都是首先初始化為一個常數，gb是根據一階導數ri，xgboost是根據一階導數gi和二階導數hi，迭代生成基學習器，相加更新學習器。
xgboost與gdbt除了上述三點的不同，xgboost在實現時還做了許多優化：
- 在尋找最佳分割點時，考慮傳統的列舉每個特徵的所有可能分割點的貪心法效率太低，xgboost實現了一種近似的演算法。大致的思想是根據百分位法列舉幾個可能成為分割點的候選者，然後從候選者中根據上面求分割點的公式計算找出最佳的分割點。
- xgboost考慮了訓練資料為稀疏值的情況，可以為缺失值或者指定的值指定分支的預設方向，這能大大提升演算法的效率，paper提到50倍。
- 特徵列排序後以塊的形式儲存在記憶體中，在迭代中可以重複使用；雖然boosting演算法迭代必須序列，但是在處理每個特徵列時可以做到並行。
- 按照特徵列方式儲存能優化尋找最佳的分割點，但是當以行計算梯度資料時會導致記憶體的不連續訪問，嚴重時會導致cache miss，降低演算法效率。paper中提到，可先將資料收集到執行緒內部的buffer，然後再計算，提高演算法的效率。
- xgboost 還考慮了當資料量比較大，記憶體不夠時怎麼有效的使用磁碟，主要是結合多執行緒、資料壓縮、分片的方法，儘可能的提高演算法的效率。
參考資料：