2. 程式人生 > >ml課程：決策樹、隨機森林、GBDT、XGBoost相關（含程式碼實現）

ml課程：決策樹、隨機森林、GBDT、XGBoost相關（含程式碼實現）

阿新 • • 發佈：2018-11-25

以下是我的學習筆記，以及總結，如有錯誤之處請不吝賜教。

基礎概念：

熵Entropy：是衡量純度的一個標準,表示式可以寫為：

資訊增益Information Gain：熵變化的一個量，表示式可以寫為：

資訊增益率Gain Ratio：資訊增益的變化率，表示式可以寫為：

基尼係數Gini Index：Gini（D）越小，資料集D的純度越高，具體表達式如下：

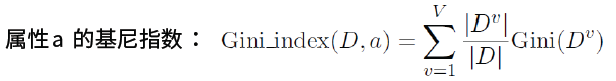
實際上基尼指數、熵、分類誤差率三者之間數學關係是統一的，將f(x)=-lnx在x=1處一階泰勒展開，忽略高階無窮小，可以得到f(x)\approx1-x：

總體流程：

決策樹遵循‘分而治之（divide and conquer）’的思想：

  • 自根至葉的遞迴過程
  • 在每個中間節點尋找一個‘劃分’屬性

三種停止條件：

  • 當前節點包含的樣本全屬於同一類別，無需劃分
  • 當前屬性集為空，或是所有樣本在所有屬性上取值相同，無法劃分
  • 當前節點包含的樣本集合為空，不能劃分

常見演算法：

ID3演算法：是根據資訊增益來選擇節點屬性。

  1. 對當前樣本集合，計算所有屬性的資訊增益；
  2. 選擇資訊增益最大的屬性作為測試屬性，把測試屬性取值相同的樣本劃為同一子樣本集；
  3. 若子樣本集的類別屬性只含有單個屬性，則分支為子葉結點，判斷其屬性值並標上相應的符號，然後返回呼叫處；否則對子樣本集遞迴呼叫本演算法。

但是ID3演算法有bug，就是容易將日期、排序等數目較多的屬性有所偏好，那麼就容易過擬合，如下圖：

因此我們常常用剪枝Prune的方法來避免過擬合。

核心程式碼：


#先計算各類別出現頻率(作為概率pi)，然後呼叫資訊熵公式計算 #H(D)-= (pi*logpi)
def calEntropy(dataset):
    n=len(dataset)
    labelCounts={}
    
    #對資料集各資料的類別計數
    for data in dataset:
        datalabel=data[-1] #取data最後一列，類別列
        if datalabel not in labelCounts.keys():
            labelCounts[datalabel]=0
        labelCounts[datalabel]+=1
    
    entropy=0.0
    
    #計算各類別出現頻率(作為概率pi),呼叫資訊熵公式計算 H(D)-=(pi*logpi)
    for key in labelCounts.keys():
        prob=float(labelCounts[key])/n
        entropy -= prob*log(prob,2)
    return entropy

C4.5演算法:使用資訊增益率選擇節點屬性。它是一種啟發式的演算法：先從劃分屬性中找出資訊增益高於平均水平的，在從中選取資訊增益率最高的。因此它可以既可以處理離散的屬性，也可以處理連續值屬性，具體過程和ID3相似。

CART演算法：使用基尼係數選擇節點屬性，通過在候選屬性集合中，選取那個使劃分後基尼係數最小的屬性。它是一種二叉樹；也是一種十分有效的分引數分類和迴歸方法，當終節點是連續變數時，該樹為迴歸樹；當終節點是分類變數時，該樹為分類樹。

以下是三個演算法的統計表格：

關於決策樹的優劣比較：

迴歸樹：基於cart演算法我們推出了樹迴歸演算法。它的構建方法具體如下：

假設一個迴歸問題，預估結果y\epsilonR,特徵向量為X=[x1,x2,x3...xp]\epsilonR,迴歸樹的兩個步驟是：

  1. 把整個特徵空間X切分成J個沒有重疊的區域R1,R2,R3...Rj
  2. 其中區域Rj中的每個樣本我們都給一樣的預測結果\tilde{y_{Rj}} = \frac{1}{n}\sum_{j\in Rj}y_{i}，其中n是Rj中的總樣本數。

因此我們就是為了找到如下RSS最小的劃分方式R1,R2,R3...RJ:

但是這個過程計算量太大了，因此我們採用探索式遞迴二分類解決這個問題。

遞迴二分：

  • 自頂向下的貪婪是遞迴方案：
  1. 自頂向下：從所有樣本開始，不斷從當前位置，把樣本切分到2個分支裡
  2. 貪婪：每一次的劃分，只考慮當前最優，而不回過頭考慮之前的劃分
  • 選擇切分的維度（特徵）xj以及切分點s是的劃分後的數RSS結果最小：

迴歸樹剪枝：如果讓迴歸樹充分生長，會有過擬合的風險，因此我們新增正則化進行限制，考慮剪枝後得到的子樹{T_{\alpha }},其中\alpha是正則化係數，當固定一個\alpha後，最佳的T_{\alpha }就是是的下列獅子子值最小的子樹：

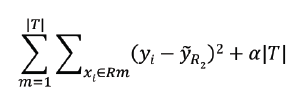
其中：|T|是迴歸樹葉子節點個數，\alpha可以通過交叉驗證選擇。

核心程式碼：

#二分資料
def binSplitDataSet(dataset,feat,val):
    mat0=dataset[nonzero(dataset[:,feat]>val)[0],:] #陣列過濾選擇特徵大於指定值的資料
    mat1=dataset[nonzero(dataset[:,feat]<=val)[0],:] #陣列過濾選擇特徵小於指定值的資料
    return mat0,mat1

#定義迴歸樹的葉子(該葉子上各樣本標籤的均值)
def regLeaf(dataset):
    return mean(dataset[:,-1])

#定義連續資料的混亂度(總方差，即連續資料的混亂度=(該組各資料-該組資料均值)**2，即方差*樣本數)）
def regErr(dataset):
    return var(dataset[:-1])*shape(dataset)[0]

#最佳特徵以及最佳特徵值選擇函式
def chooseBestSplit(dataset,leafType=regLeaf,errType=regErr,ops=(1,4)):
    tolS=ops[0];tolN=ops[1];m,n=shape(dataset)
    S=errType(dataset);bestS=inf;beatIndex=0;bestVal=0
    if len(set(dataset[:,-1].T.tolist()[0]))==1: #若只有一個類別
        return None,leafType(dataset)
    for featIndex in range(n-1):
        for splitVal in set(dataset[:,featIndex].T.tolist()[0]):
            mat0,mat1=binSplitDataSet(dataset,featIndex,splitVal)
            #若切分後兩塊資料的最少樣本數少於設定值，不切分
            if (shape(mat0)[0]<tolN) or (shape(mat1)[0]<tolN): 
                continue
            newS=errType(mat0)+errType(mat1)
            if newS<bestS:
                bestIndex=featIndex;bestVal=splitVal;bestS=newS
    #若以最佳特徵及特徵值切分後的資料混亂度與原資料混亂度差值小於閾值，不切分
    if (S-bestS)<tolS:
        return None,leafType(dataset)
    mat0,mat1=binSplitDataSet(dataset,bestIndex,bestVal)
    #若以最佳特徵及特徵值切分後兩塊資料的最少樣本數少於設定值，不切分
    if (shape(mat0)[0]<tolN) or (shape(mat1)[0]<tolN):
        return None,leafType(dataset)
    return bestIndex,bestVal

"""構建迴歸樹"""
def createTree(dataset,leafType=regLeaf,errType=regErr,ops=(1,4)):
    feat,val=chooseBestSplit(dataset,leafType,errType,ops)
    if feat==None:
        return val
    regTree={}
    regTree['spFeat']=feat
    regTree['spVal']=val
    lSet,rSet=binSplitDataSet(dataset,feat,val)
    regTree['left']=createTree(lSet,leafType,errType,ops)
    regTree['right']=createTree(rSet,leafType,errType,ops)
    return regTree

決策樹的整合Ensemble:

首先要說下Booststraping思想：這個名字來自成語‘pull up by your own booststraps’,意思是靠你自己的資源，簡稱自助法，他是一種又放回的抽樣方法，是非引數統計中一種重要的估計統計量方差而進行區間估計量的統計方法。該方法在小樣本時效果很好，通過方差的估計可以構造置信區間。核心步驟如下：

  1. 採用重複抽樣技術從原始樣本中抽取一定數量（自己給定）的樣本，此過程允許重複抽樣。
  2. 根據抽出的樣本計算給定的統計量T.
  3. 重複上述N次（一般大於1000），得到N個統計量T。
  4. 計算上述N個統計量T的樣本方差，得到統計量的方差。

 

Bagging演算法:是boostrap aggregating的縮寫，使用了上述的bootstraping思想，可以降低過擬合的風險，提高泛化能力，具體流程如下：

  1. 輸入樣本集D={(x,y1),(x2,y2),...(xm,ym)}
  2. 對於t = 1,2，... ，T:

        a）對訓練集進行第t次隨機取樣，共採集m次，得到包含m個樣本的取樣集Dm

        b）用取樣集Dm訓練第m個基學習器Gm（x）

    3.分類場景，則T個學習器投出最多票數的類別為最終類別。迴歸場景，T個學習器得到的迴歸出結果進行算數平均得到的值為最終的模型輸出。 

 隨機森林RandomForest演算法：與Bagging基本類似，使用了CART決策樹作為基學習器，不同點在於bagging是隨機抽取樣本，而隨機森林是對樣本、屬性都進行隨機抽取。

  1. 從原始訓練集中，應用boostrap方法有放回的隨機抽取k個新的自助樣本集，並由此構建k棵分類迴歸樹，每次未被抽到的樣本組成了k個袋外資料（out-of-bag）
  2. 設有n個特徵，則在每一個樹的每個節點處隨機抽取m個特徵，通過計算每個特徵蘊含的資訊量，特徵中選擇一個最具有分類能力的特徵進行節點分裂。
  3. 每棵樹最大限度的生長，不做任何剪裁。
  4. 將生成的最多棵樹組成隨機森林，用隨機森林對新的資料進行分類，分類結果按分類器投票多少而定。迴歸場景，T個基模型（迴歸樹）得到的迴歸結果進行算術平均得到的值為最終的模型輸出。

Boosting演算法：與之前兩種演算法不同，具體流程如下：

  1. 先在原資料集長出一個樹
  2. 把先前一個樹沒能完美分類的資料重新weight
  3. 用新的re-weighted 樹在訓練出一個樹
  4. 最終的分類結果由加權投票決定

公式：

Adaboost演算法：這個演算法是boosting演算法的實現之一，也是比較常用的演算法，具體流程如下：

  1. 初始化訓練資料的權值分佈，每一個訓練樣本最開始時都被賦予相同的權值：1/n

  2. 進行多輪迭代，用m=1,2，...，m表示迭代的第多少輪：

        a）使用具有權值分佈Dm的訓練集學習，得到基本分類器（選取讓誤差率最低的閾值來設計基本分類器）：

        b）計算Gm在訓練資料集上的分類誤差率（Gm在訓練資料集上的誤差率em就是被Gm誤分類樣本的權值之和），這裡I表示0或者1取值，\omega _{mi}表示錯誤的次數：

        c）計算Gm的係數，\alpha _{m}表示Gm在最終分類器中的重要程度（得到基本分類器在最終分類器中所佔的權重），e_{m}<=\frac{1}{2}時，\alpha _{m}>=0,且\alpha _{m}隨著e_{m}的減小而增大，意味著分類誤差率越小的分類器在最終分類器中的作用越大：

        d）更新訓練資料集的權值分佈（為了得到樣本的新的權值分佈），用於下一輪迭代。

使得被基本分類器Gm誤分類樣本的權值增大，而被正確分類樣本的權值減小。通過這樣的方式，Adaboost能重點關注於那些較難分的樣本上。

其中：Zm表示規範化因子，使得D_{m+1}成為一個概率分佈。

    3.組合各個弱分類器：

    得到最終分類器，如下：

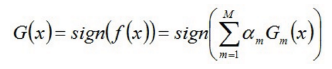
核心程式碼：

#label為樣本標籤，shape=(1,m)
def adaBoostTrainDS(dataArr,classLabels,numIt=40):
    weakClassArr=[];m=shape(dataArr)[0]
    D=mat(ones((m,1))/m) #初始化樣本權重
    aggClassEst=mat(zeros((m,1)))
    for i in range(numIt):
        bestStump,error,classEst=buildStump(dataArr,classLabels,D)
        alpha = float(0.5*log((1.0-error)/max(error,1e-16))) #max(error,1e-16)防止0誤差的計算溢位
        bestStump["alpha"]=alpha
        weakClassArr.append(bestStump)
        #print ("D:",D.T,"\n","predClass:",classEst.T)
        
        #為下一次迭代更新D(很關鍵，矩陣運算容易寫錯！)
        expon=multiply(-1*alpha*mat(classLabels).T,classEst) #shape(5,1)*shape(5,1)對應元素相乘，得到各樣本的-alpha*yi*G(xi)
        D=multiply(D,exp(expon)) #shape(5,1)*shape(5,1)對應元素相乘，
        D=D/D.sum() #得到各樣本更新後的wi
        
        #計算彙集的分類結果aggClassEst(即，將每次最佳決策樹分類結果bestClass*alpha相加)
        aggClassEst+=alpha*classEst
        #print("aggClassEst:",aggClassEst.T)
        aggErrors=multiply(sign(aggClassEst)!=mat(classLabels).T,ones((m,1)))
        errorRate=aggErrors.sum()/m
        #print("total error:",errorRate)
        if errorRate==0.0:
            break
    return weakClassArr,errorRate,aggClassEst

GBDT演算法（Gradient Boosted Decison Tree）：是Adaboost的迴歸版本，是將原來adaboost中0或者1的誤差率的計算，變成err這個計算（err代表多種誤差計算，例如前面說過的平方誤差，log誤差等等），具體公式如下：

計算得到的殘差，作為下一輪迭代的學習目標，最終的結果有加權和值得到，不在是簡單的多數投票：

XGBoost演算法（Extreme GBoosted）：從名字可以看出，該演算法是GBDT的高階版，它是將GBDT的速度和效率做到了極致。主要變化如下：

  1. 使用L1和L2正則化防止過擬合：

  2. 對代價函式進行一階和二階求導，更快的收斂；
  3. 對其進行從下之上的剪枝，防止演算法貪婪。

後續我們會繼續學習如何對XGboost及GBDT等整合演算法進行引數調節，To be continue......

相關推薦

ml課程：決策樹、隨機森林、GBDT、XGBoost相關（含程式碼實現）

以下是我的學習筆記，以及總結，如有錯誤之處請不吝賜教。 基礎概念： 熵Entropy：是衡量純度的一個標準,表示式可以寫為： 資訊增益Information Gain：熵變化的一個量，表示式可以寫為： 資訊增益率Gain Ratio：資訊增益的變化率，表示式可以寫為：

ml課程：概率圖模型—貝葉斯網路、隱馬爾可夫模型相關（含程式碼實現）

以下是我的學習筆記，以及總結，如有錯誤之處請不吝賜教。 本文主要介紹機器學習中的一個分支——概率圖模型、相關基礎概念以及樸素貝葉斯、隱馬爾可夫演算法，最後還有相關程式碼案例。 說到機器學習的起源，可以分為以下幾個派別： 連線主義：又稱為仿生學派(bionicsism)或生理學派

ml課程：SVM相關（含程式碼實現）

以下是我的學習筆記，以及總結，如有錯誤之處請不吝賜教。 本文主要介紹svm的創始人Vapnik‘s如何一步一步構建出這個經典演算法模型的，同時也可以給我們以後演算法之路提供一個思路，即使你對優化等數學方法不熟悉，依然可以創造出很好的演算法。 下svm關鍵的幾個idea： KEY ID

ml課程：線性迴歸、邏輯迴歸入門（含程式碼實現）

以下是我的學習筆記，以及總結，如有錯誤之處請不吝賜教。 本文主要介紹簡單的線性迴歸、邏輯迴歸先關推倒，以及案例程式碼。 昨天做專案發現K-means都忘了，想想之前很多基礎都忘了，於是決定重新開始學一遍ml的基礎內容，順便記錄一下，也算是梳理自己的知識體系吧。 機器學習：目前包括有監

ml課程：最大熵與EM演算法及應用（含程式碼實現）

以下是我的學習筆記，以及總結，如有錯誤之處請不吝賜教。 本文主要介紹最大熵模型與EM演算法相關內容及相關程式碼案例。 關於熵之前的文章中已經學習過，具體可以檢視：ml課程：決策樹、隨機森林、GBDT、XGBoost相關（含程式碼實現），補充一些 基本概念： 資訊量：資訊的度量，即

ml課程：聚類概述及K-means講解（含程式碼實現）

以下是我的學習筆記，以及總結，如有錯誤之處請不吝賜教。 本文主要介紹聚類以及K均值演算法的推倒過程，最後有相關程式碼案例。 說到聚類就不得不先說說機器學習的分類。 機器學習主要分為三類： 監督學習：分類、迴歸... 無監督學習：聚類、降維... 強化學習。  

乾貨｜從決策樹到隨機森林：樹型演算法的實現原理與Python 示例

原文地址 基於樹（Tree based）的學習演算法在資料科學競賽中是相當常見的。這些演算法給預測模型賦予了準確性、穩定性以及易解釋性。和線性模型不同，它們對非線性關係也能進行很好的對映。常見的基於樹的模型有：決策樹、隨機森林和提升樹。 在本篇文章中，我們將會介紹決策

機器學習(五)：通俗易懂決策樹與隨機森林及程式碼實踐

與SVM一樣，決策樹是通用的機器學習演算法。隨機森林，顧名思義，將決策樹分類器整合到一起就形成了更強大的機器學習演算法。它們都是很基礎但很強大的機器學習工具，雖然我們現在有更先進的演算法工具來訓練模型，但決策樹與隨機森林因其簡單靈活依然廣受喜愛，建議大家學習。 # 一、決策樹 ## 1.1 什麼是決策樹

決策樹與隨機森林

隨機 tro 過程 能夠 ots pull 葉子節點 合並 pan 決策樹 　　決策樹學習采用的是自頂向下的遞歸方法, 其基本思想是以信息熵為度量構造一棵熵值下降最快的樹,到葉子節點處的熵值為零, 　　此時每個葉節點中的實例都屬於同一類。 決策樹三種生成算法 ID3 -

機器學習之決策樹與隨機森林模型

會有 strong pytho red -s 很多 4.5 是我 機器 歡迎大家前往騰訊雲技術社區，獲取更多騰訊海量技術實踐幹貨哦~ 作者：汪毅雄 導語 本文用容易理解的語言和例子來解釋了決策樹三種常見的算法及其優劣、隨機森林的含義，相信能幫助初學者真正地理解相關知識

[三]機器學習之決策樹與隨機森林

3.1 目標任務 1.學習決策樹和隨機森林的原理、特性 2.學習編寫構造決策樹的python程式碼 3.學習使用sklearn訓練決策樹和隨機森林，並使用工具進行決策樹視覺化 3.2 實驗資料 資料集：鳶尾花資料集，詳情見[機器學習之迴歸]的Logistic迴歸實驗 3.3

R語言︱決策樹族——隨機森林演算法

筆者寄語：有一篇《有監督學習選擇深度學習還是隨機森林或支援向量機?》（作者Bio：SebastianRaschka）中提到，在日常機器學習工作或學習中，當我們遇到有監督學習相關問題時，不妨考慮下先用簡單的假設空間（簡單模型集合），例如線性模型邏輯迴歸。若效果不好，也即並沒達到你的預期或評判效果基

在OpenCV中實現決策樹和隨機森林

目錄 1.決策樹 2.隨機森林 1.決策樹 需要注意的點： Ptr<TrainData> data_set = TrainData::loadFromCSV("mushroom.data",//檔名

機器學習——決策樹和隨機森林演算法

認識決策樹 決策樹思想的來源非常樸素，程式設計中的條件分支結構就是if-then結構，最早的決策樹就是利用這類結構分割資料的一種分類學習方法。 下面以一個問題引出決策樹的思想 這個問題用圖來表示就是這樣: 為什麼先把年齡放在第一個呢，下面就是一個概念:資訊熵 資訊熵

【機器學習】決策樹與隨機森林（轉）

文章轉自： https://www.cnblogs.com/fionacai/p/5894142.html    首先，在瞭解樹模型之前，自然想到樹模型和線性模型有什麼區別呢？其中最重要的是，樹形模型是一個一個特徵進行處理，之前線性模型是所有特徵給予權重相加得到一個新的值。決

【線上直播】決策樹與隨機森林

講師：段喜平   講師簡介： 研究生畢業於中山大學，曾就職於華為，百分點等公司，目前在魅族擔任NLP演算法工程師。   分享大綱： 1. 樹模型簡介 2. 常用決策樹演算法ID3, C4.5, CART，隨機森林等演算法介紹 3. 隨機森林程

決策樹之隨機森林

一、簡單介紹 1、Bootstraping 一種有放回抽樣的選擇訓練樣本資料的方法。 2、Bagging策略 二、隨機森林 一個樣本集合中有n個樣本，用Bootstrap方法對它取樣m次就會得到m個有n個樣本的樣本集合，就等於得到了m個訓練資料集。對於每一個訓

《web安全之機器學習入門》第6章決策樹與隨機森林演算法

決策樹識別pop3埠掃描（原書中識別暴力破解，實際上pop3協議的並沒有guess_passwd型別的資料，所以改為識別port_sweep.）：待分析資料集：KDD-99資料集，連結：http://kdd.ics.uci.edu/databases/kddcup99/kdd

決策樹和隨機森林演算法

決策樹和隨機森林都是常用的分類演算法，它們的判斷邏輯和人的思維方式非常類似，人們常常在遇到多個條件組合問題的時候，也通常可以畫出一顆決策樹來幫助決策判斷。本文簡要介紹了決策樹和隨機森林的演算法以及實現，並使用隨機森林演算法和決策樹演算法來檢測FTP暴力破解和PO

Spark2.0機器學習系列之3：決策樹及Spark 2.0-MLlib、Scikit程式碼分析

概述 分類決策樹模型是一種描述對例項進行分類的樹形結構。 決策樹可以看為一個if-then規則集合，具有“互斥完備”性質 。決策樹基本上都是 採用的是貪心（即非回溯）的演算法，自頂向下遞迴分治構造。 生成決策樹一般包含三個步驟： 特徵選擇 決策樹生成 剪枝