機器學習 --- 深度前饋網路
對於某些問題,其特徵的表述極其困難,比如人臉的識別,其影響因素可能涉及到角度,光影,顏色,形狀等。深度學習旨在將原複雜的對映關係分解成一系列巢狀的簡單對映。
一、深度前饋網路簡要
深度前饋網路又稱多層感知機(MLP),對於分類器,函式 將輸入
對映到類別
上。而MLP定義了一個對映
,通過學習引數
,以達到最佳近似
的效果。由於模型的輸出和模型本身沒有反饋連線,所以稱作前饋神經網路,例如卷積神經網路(在之後的文章中會詳細說明,本次先說明神經網路的基礎部分)。
二、深層神經網路的直觀理解
深層神經網路(Deep Neural Network)模型圖
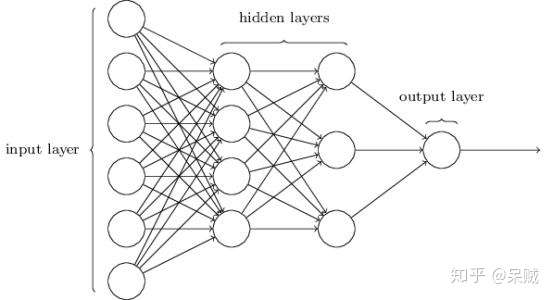
神經網路分為三層:輸入層、隱藏層、輸出層。網路模型通過一個有向無環圖關聯,圖中描述了各節點(函式)如何複合在一起
深度學習中,網路即意味著將很多不同的函式複合在一起,以能達到表示複雜問題的能力。
網路模型通過一個有向無環圖關聯,圖中描述了各節點(函式)如何複合在一起能得到最佳的函式的近似效果。整個網路工作的流程從圖中反應就是,變數 的特徵屬性匯入至輸入層,通過隱藏層內部的計算,從輸出層匯出輸出結果
網路模型中含有很多層次,每個層次可以抽象成函式 ,其中
表示當前層數,相對於最開始的模型圖,可以得到一個鏈式結構:
,對於某層來說,上層的輸出作為該層的輸入。
三、神經節點
網路模型中含有多個節點,這形象的稱作"神經元",又稱"神經節點"。神經節點的意義其實就類似於之前提到的多個函式複合(這裡是神經節點之間通過某種規則互連),而單個神經節點又是最基本的函式。除輸入層外,每個神經節點根據功能的劃分一般有線性函式
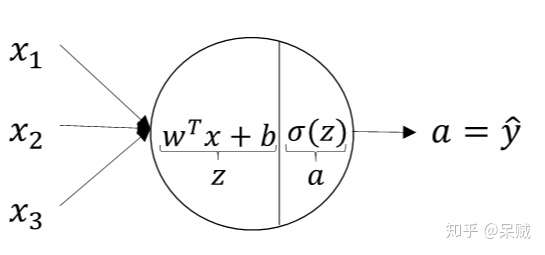
上圖中 屬於線性部分,
為上層的輸出,作為本層的輸入。之後經過一個啟用函式
,因此每個神經元的資訊主要包括有引數
和選取哪個啟用函式。
四、啟用函式
啟用函式負責將神經節點的輸入對映到輸出端上,如果不使用啟用函式,那麼無論神經網路有多少層,都是輸入的線性組合,因此不能解決非線性問題。
列舉一些常用的啟用函式:
Sigmoid:

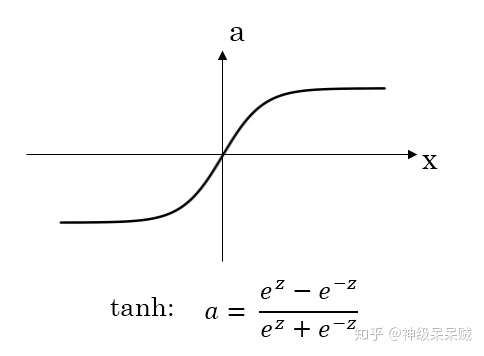
雙曲正切:
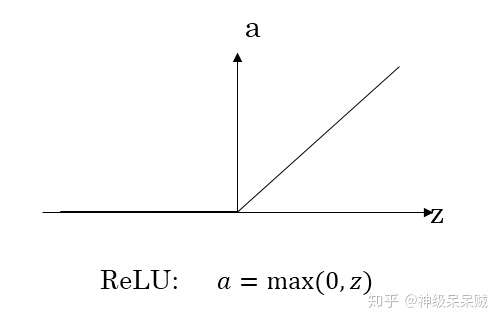
線性整流:
滲漏整流線性:
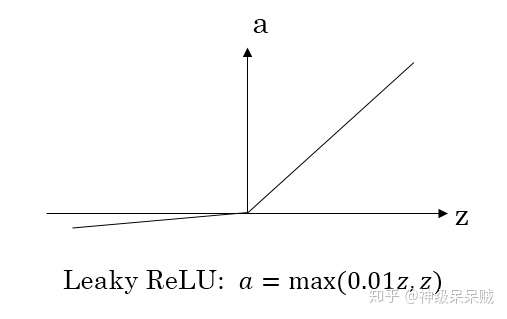
softmax:
五、代價函式
1.代價函式概述
網路模型通過學習演算法,在資料集上訓練模型,發掘 的對映關係。引入代價函式評估演算法效能,為學習演算法指明優化方向。這樣來說,引數模型經過訓練樣本定義了一個分佈
,所以使用最大似然原理估計模型引數。
2.交叉熵代價函式
以二分類問題為例,其符合伯努利分佈,對樣本 有:
因此樣本 的分佈律是:
由似然函式:
為了構建近似樣本真實的概率分佈,需要取似然函式的最大值,因此對似然函式兩邊取對數並乘以-1,即最小化下面的式子:
該式子稱作交叉熵代價函式,常用作二分類問題,此時神經網路輸出層一般會選擇Sigmoid作為啟用函式。觀察上式,直觀地理解下,當出現預測錯誤,交叉熵代價函式的值將會變得非常大。
3.對數釋然代價函式
對於多分類問題,輸出層一般會選擇softmax作為啟用函式。此時代價函式一般選擇對數釋然代價函式,對共有 個類別問題有:
注意:這裡為什麼不選擇均方誤差代價函式的原因在於,使用均方誤差代價函式容易造成softmax和sigmoid運算單元的飽和現象,這樣不利於基於梯度的學習方法,使用上述函式可以消去函式中的指數運算從而有利於梯度學習過程。
六、正向傳播
神經網路的訓練過程主要分為正向傳播和反向傳播過程。
1.正向傳播
假定輸入矩陣 ,即有
個樣本,
個特徵值。正向傳播過程中,對於第
層(第0層為輸入層),有:
其中 表示第
層啟用函式。當傳至輸出層時,此時:
2.正向傳播示例
假設網路模型如下圖所示,網路共有 層
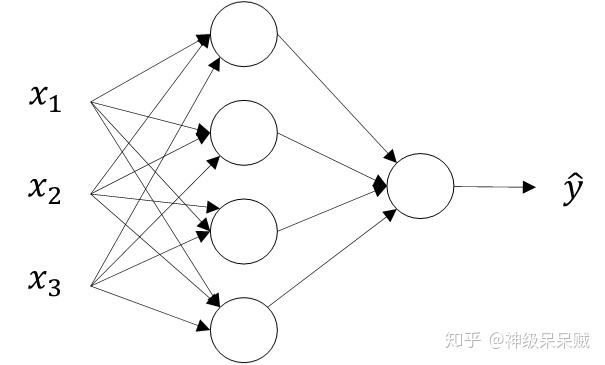
輸入矩陣維度表示成:
對於第 層:
第一層向第二層傳播過程:
第二層向第三層傳播過程:
七、反向傳播

反向傳播是根據代價函式通過鏈式求導算得,以上圖的網路模型圖作為示例,此處是針對二分類問題(選用交叉熵代價函式,輸出層啟用函式sigmoid):
正向傳播過程:
反向傳播過程:
表示點乘
表示矩陣乘法
一次迴圈開始-----------------------------------------
(這裡解釋一下為什麼乘以 ,因為在正向傳播中,
的矩陣乘法過程相當於將
樣本的結果壓縮到矩陣
中,反向傳播過程可看成一個逆向的過程)
一次迴圈結束-----------------------------------------
所以,整個反向傳播演算法的過程:
八、程式碼
為了更清晰的表示這些傳播過程,下面使用python程式碼來具體體現(來自Andrew ng 作業):
import numpy as np
def sigmoid(Z):
cache = Z
A = 1.0 / (1 + np.exp(-Z))
assert(A.shape == Z.shape)
return A, cache
def sigmoid_derivative(dA,cache):
Z = cache
f = 1.0 / (1 + np.exp(-Z))
dZ = dA * f * (1 - f)
assert(dZ.shape == Z.shape)
return dZ
def ReLU(Z):
cache = Z
A = np.maximum(0, Z)
assert(A.shape == Z.shape)
return A, cache
def ReLU_derivative(dA,cache):
Z = cache
dZ = np.array(dA, copy = True)
dZ[Z <= 0] = 0
assert(dZ.shape == Z.shape)
return dZ
# 初始化引數
def initialize_parameters(layer):
np.random.seed(1)
parameters = {}
L = len(layer)
for i in range(1,L):
parameters["W" + str(i)] = np.random.randn(layer[i], layer[i-1]) * np.sqrt(1 / layer[i-1])
parameters["b" + str(i)] = np.zeros((layer[i], 1))
assert(parameters["W" + str(i)].shape == (layer[i], layer[i-1]))
assert(parameters["b" + str(i)].shape == (layer[i], 1))
return parameters
# 正向線性化
def linear_forward(A_prev, W, b):
Z = np.dot(W, A_prev) + b
assert(Z.shape == (W.shape[0], A_prev.shape[1]))
cache = (A_prev, W, b)
return Z,cache
# 正向啟用
def linear_forward_activation(A_prev, W, b, activation_function):
if activation_function == 'sigmoid':
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = sigmoid(Z)
elif activation_function == 'ReLU':
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = ReLU(Z)
assert(A.shape == (W.shape[0], A_prev.shape[1]))
cache = (linear_cache, activation_cache)
return A, cache
# 正向傳播
def L_model_forward(X, parameters):
A = X
L = len(parameters) // 2
caches = []
# 輸入層與隱藏層正向傳播
for i in range(1, L):
A_prev = A
A, cache = linear_forward_activation(A_prev, parameters['W' + str(i)], parameters['b' + str(i)], 'ReLU')
caches.append(cache)
# 輸出層正向傳播
AL, cache = linear_forward_activation(A, parameters['W' + str(L)], parameters['b' + str(L)],'sigmoid')
caches.append(cache)
assert(AL.shape == (1, X.shape[1]))
return AL, caches
# 計算成本函式
def compute_cost(AL, Y):
m = Y.shape[1]
cost = -np.sum(np.multiply(np.log(AL),Y) + np.multiply(np.log(1 - AL), 1 - Y)) / m
cost = np.squeeze(cost)
return cost
# 反向線性傳播
def linear_backward(dZ, cache):
A_prev, W, b = cache
m = A_prev.shape[1]
dW = 1.0 / m * np.dot(dZ, A_prev.T)
db = 1.0 / m * np.sum(dZ, axis = 1, keepdims = True)
dA_prev = np.dot(W.T, dZ)
assert(dW.shape == (dZ.shape[0], A_prev.shape[0]))
assert(db.shape == db.shape)
assert(dA_prev.shape == (W.T.shape[0], dZ.shape[1]))
return dA_prev, dW, db
# 反向啟用
def linear_backward_activation(dA, cache, function_activation):
linear_cache, activation_cache = cache
if function_activation == 'sigmoid':
dZ = sigmoid_derivative(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
elif function_activation == 'ReLU':
dZ = ReLU_derivative(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
return dA_prev, dW, db
# 反向傳播
def L_model_backward(Y, AL, caches):
grads = {}
L = len(caches)
Y = Y.reshape(AL.shape)
dAL = -(np.divide(Y, AL) - np.divide(1-Y, 1-AL))
grads['dA' + str(L)], grads['dW' + str(L)], grads['db' + str(L)] = \
linear_backward_activation(dAL, caches[L-1], 'sigmoid')
for i in reversed(range(L - 1)):
grads['dA' + str(i + 1)], grads['dW' + str(i + 1)], grads['db' + str(i + 1)] = \
linear_backward_activation(grads['dA' + str(i + 2)], caches[i],'ReLU')
return grads
# 引數更新
def updata_parameters(parameters, grads, learning_rate):
L = len(parameters) // 2
for i in range(L):
parameters['W' + str(i + 1)] = parameters['W' + str(i + 1)] \
- learning_rate * grads['dW' + str(i + 1)]
parameters['b' + str(i + 1)] = parameters['b' + str(i + 1)] \
- learning_rate * grads['db' + str(i + 1)]
return parameters
# 輸出結果評估
def predict(X, y, parameters, print_result = True):
m = X.shape[1]
p = np.zeros((1, m))
AL, caches = L_model_forward(X, parameters)
for i in range(m):
if AL[0, i] > 0.5:
p[0,i] = 1
elif AL[0, i] < 0.5:
p[0, i] = 0
if print_result == True:
print("Accuracy:" + str(np.sum(p == y) / m))
return p
# 神經網路傳播
def L_layer_model(X, Y, layer, iteration, learning_rate):
costs = []
parameters = initialize_parameters(layer)
for i in range(0, iteration):
AL, caches = L_model_forward(X, parameters)
cost = compute_cost(AL, Y)
grads = L_model_backward(Y, AL, caches)
parameters = updata_parameters(parameters, grads, learning_rate)
if i % 100 == 0:
print("cost after iteration %d:%f" %(i, cost))
costs.append(cost)
plt.plot(np.squeeze(costs))
plt.xlabel('iteration')
plt.ylabel('cost')
plt.title('learning-rate:' + str(learning_rate))
plt.show()
return parameters