貝葉斯網路

貝葉斯網路（Bayesian Networks）也被稱為信念網路（Belif Networks）或者因果網路（Causal Networks），是描述資料變數之間依賴關係的一種圖形模式，是一種用來進行推理的模型。貝葉斯網路為人們提供了一種方便的框架結構來表示因果關係，這使得不確定性推理變得在邏輯上更為清晰、可理解性強。

對於貝葉斯網路，我們可以用兩種方法來看待它：首先貝葉斯網表達了各個節點間的條件獨立關係，我們可以直觀的從貝葉斯網當中得出屬性間的條件獨立以及依賴關係；另外可以認為貝葉斯網用另一種形式表示出了事件的聯合概率分佈，根據貝葉斯網的網路結構以及條件概率表（CPT）我們可以快速得到每個基本事件（所有屬性值的一個組合）的概率。貝葉斯學習理論利用先驗知識和樣本資料來獲得對未知樣本的估計，而概率（包括聯合概率和條件概率）是先驗資訊和樣本資料資訊在貝葉斯學習理論當中的表現形式。

注： 在概率論中，聯合概率是指在多元的概率分佈中多個隨機變數分別滿足各自條件的概率。舉例說明：假設X和Y都服從正態分佈，那麼P{X<4,Y<0}就是一個聯合概率，表示X<4,Y<0兩個條件同時成立的概率。 聯合概率：表示兩個事件共同發生的概率。A與B的聯合概率表示為 P(AB) 或者P(A,B),或者P（A∩B）

貝葉斯網路由以下兩部分組成：

一 貝葉斯網路結構

貝葉斯網的網路結構是一個有向無環圖（Directed Acyclic Graph），其中每個結點代表一個屬性或者資料變數，結點間的弧代表屬性（資料變數） 間的概率依賴關係。一條弧由一個屬性（資料變數）A指向另外一個屬性（資料變數）B說明屬性A的取值可以對屬性B的取值產生影響，由於是有向無環圖，A、B間不會出現有向迴路。在貝葉斯網當中，直接的原因結點（弧尾）A叫做其結果結點（弧頭）B的雙親結點（parents），B叫做A的孩子結點（children）。如果從一個結點X有一條有向通路指向Y，則稱結點X為結點Y的祖先（ancestor），同時稱結點Y為結點X的後代（descendent）。
我們用下面的例子來具體說明貝葉斯網的結構：

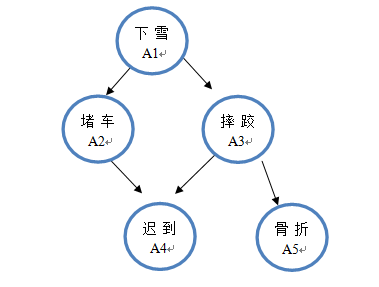
圖1 簡單的貝葉斯網模型

圖1 中共有五個結點和五條弧。下雪A1是一個原因結點，它會導致堵車A2和摔跤A3。而我們知道堵車A2和摔跤A3都可能最終導致上班遲到A4。另外如果在路上摔跤嚴重的話還可能導致骨折A5。這是一個簡單的貝葉斯網路的例子。在貝葉斯網中像A1這樣沒有輸入的結點被稱作根結點（root），其他結點被統稱為非根結點。

貝葉斯網路當中的弧表達了結點間的依賴關係，如果兩個結點間有弧連線說明兩者之間有因果聯絡，反之如果兩者之間沒有直接的弧連線或者是間接的有向聯通路徑，則說明兩者之間沒有依賴關係，即是相互獨立的。結點間的相互獨立關係是貝葉斯網路當中很重要的一個屬性，可以大大減少建網過程當中的計算量，同時根據獨立關係來學習貝葉斯網路也是一個重要的方法，這在本文後面會著重介紹。使用貝葉斯網路結構可以使人清晰的得出屬性結點間的關係，進而也使得使用貝葉斯網進行推理和預測變得相對容易實現。

從上圖中我們可以看出，節點間的有向路徑可以不只一條，一個祖先結點可以通過不同的途徑來影響它的後代結點。如我們說下雪可能會導致遲到，而導致遲到的直接原因可能是堵車，也可能是在雪天滑倒了、摔了一跤。這裡每當我們說一個原因結點的出現會導致某個結果的產生時，都是一個概率的表述，而不是必然的，這樣就需要為每個結點新增一個條件概率。一個節點在其雙親節點（直接的原因接點）的不同取值組合條件下取不同屬性值的概率，就構成了該結點的條件概率表。

二． 條件概率表
在上一節當中已經介紹了條件概率的概念，貝葉斯網路中的條件概率表是結點的條件概率的集合。當使用貝葉斯網路進行推理時，實際上是使用條件概率表當中的先驗概率和已知的證據結點來計算所查詢的目標結點的後驗概率的過程。

條件概率可以由某方面的專家總結以往的經驗給出(但這是非常困難的，只適合某些特殊領域)，另外一種方法就是通過條件概率公式 在大樣本資料當中統計求得，學習條件概率表的演算法將在下一節中詳細介紹。在這裡我們先根據上圖的貝葉斯網給出其中的一些條件概率表，使大家對條件概率表有一個感性的認識。
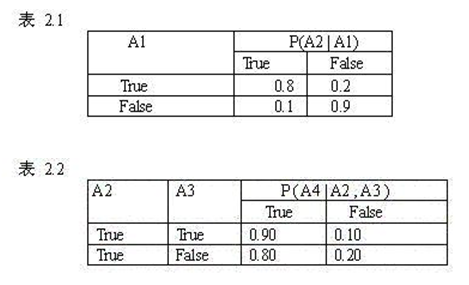
如果將結點A1下雪當作證據結點，那麼發生A2堵車的概率如何呢？下表給出了相應的條件概率：

上表是最簡單的情況，如果有不只一個雙親結點的話，那麼情況會變得更為複雜一些，見表2.2：
由表中可以看出，當堵車A2和摔跤A3取不同的屬性值時，導致遲到A4的概率是不同的。貝葉斯網條件概率表中的每個條件概率的都是以當前結點的雙親結點做為條件集的。如果一個結點有n個父節點，在最簡單的情況下（即每個結點都是二值結點，只有兩個可能的屬性值：True或者False），那麼它的條件概率表有2n 行；如果每個屬性結點有k個屬性值，則有k n行記錄，其中每行有k-1項（因為k項概率的總和為1，所以只需知道其中的k-1項，最後一項可以用減法求得），這樣該條件概率表將一共有 (k-1) k n項記錄。
根據條件概率和貝葉斯網路結構，我們不僅可以由祖先接點推出後代的結果，還可以通過後代當中的證據結點來向前推出祖先取各種狀態的概率。
貝葉斯網可以處理不完整和帶有噪聲的資料集，因此被日益廣泛的應用於各種推理程式當中。同時由於可以方便的結合已有的先驗知識，將已有的經驗與資料集的潛在知識相結合，可以彌補相互的片面性與缺點，因此越來越受到研究者的喜歡。

貝葉斯網路分類：
1。靜態貝葉斯網路
2。動態貝葉斯網路

三 動態貝葉斯網路

在我 們 這 裡所講的DBN，它的動態，並不是說網路結構隨著時間的變化而發生變化，而是樣本資料，或者說觀測資料，隨著時間的變化而變化。其中對網路結構隨時間變化的情況主要出現在這麼一個問題中：對一個未知物件集進行跟蹤。隨著時間的變化，無法知道哪些物件產生了，而哪些物件又消失了。在A工界，這類問題被稱為，’First Order”，也被稱為”Propositional”模型，相關討論可以看文獻〔35]0
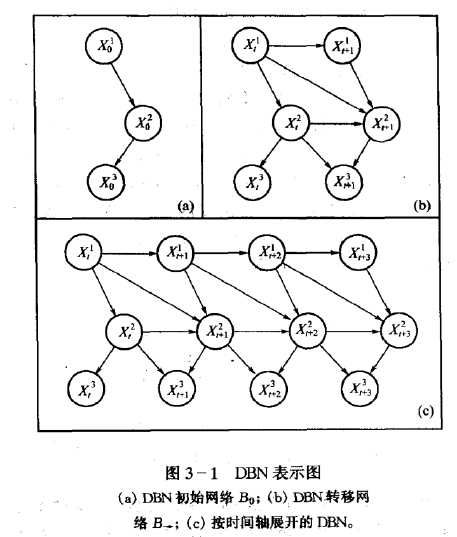
一般 的 DBN有兩個特點。網路 的 拓撲結構在每個時間片(time slice,快照) 內是相同的，而片與片之間通過類似的弧進行連線。

一個BN可以定義為：BN=（G，θ）,其中G是X上聯合概率分佈的有向非迴圈圖，θ表示網路的引數。其中，X上的聯合概率分佈定義為：

P(X1,X2,...,Xn)=∏i=inP(Xi|Pa(Xi))
DBN模型則將這種表述擴充套件到模型化含時間因素的隨機過程。為了用BN表述隨機過程，需要得到隨機變數X[1]，X[2]，...,X[n]上的一個概率分佈，但這樣一個分佈是十分複雜的。因此，為了能夠對複雜系統進行研究並建立相應的模型，需要做一些假設和簡化條件處理。
假設條件：
1 假設在一個有限時間內條件概率變化過程對所以t是一致平穩
2 假設動態概率過程是馬氏的，即滿足：
P(X[t+1]|X[1],X[2],...,X[t])=P(X[t+1]|X[t])
也就是說未來時刻的概率只與當前時刻有關而與過去時刻無關
3 假設相鄰時間的條件概率過程是平穩的，即P(X[t+1]|X[t])與時間t無關，可以容易地得到不同時間的轉移概率P(X[t+1]|X[t])

基於上述假設，建立在隨機過程時間軌跡上的聯合概率分佈的DBN就由兩部分組成：一個先驗網B0,定義在初始狀態X[1]上的聯合概率分佈；一個轉移網B→,定義在變數X[1]與X[2]上的轉移概率P(X[t+1]|X[t])（對所有的t都成立）
因此，若給定一個DBN模型，則在X[1]，X[2]，...,X[T]上的聯合概率分佈為：

P(X[1],X[2],...,X[T])=PB0(X[1])∏t=iTPB→(X[t+1]|X[t])
給出DBN定義：一個DBN可以定義為(B0,B→)。其中B0表示最開始的BN，從圖中可以得到任一節點的先驗概率P(X0)，B→表示有兩個以上時間片段的BN組成的圖形。