《推薦系統實踐》第二章利用使用者行為資料

阿新 • • 發佈：2018-11-24

2.1 使用者行為資料簡介

在電子商務網站中行為主要包括網頁瀏覽、購買、點選、評分和評論等。

使用者行為在個性化推薦系統中一般分兩種——顯性反饋行為（explicit feedback）和隱性反饋行為（implicit feedback）。顯性反饋行為包括使用者明確表示對物品喜好的行為。隱性反饋行為指的是那些不能明確反應使用者喜好的行為。最具代表性的隱性反饋行為就是頁面瀏覽行為。

按照反饋的明確性分，使用者行為資料可以分為顯性反饋和隱性反饋，但按照反饋的方向分，又可以分為正反饋和負反饋。正反饋指使用者的行為傾向於指使用者喜歡該物品，而負反饋指使用者的行為傾向於指使用者不喜歡該物品。在顯性反饋中，很容易區分一個使用者行為是正反饋還是負反饋，而在隱性反饋行為中，就相對比較難以確定。

一個使用者行為可表示為6部分，即產生行為的使用者和行為的物件、行為的種類、產生行為的上下文、行為的內容和權重。

目前比較有代表性的資料集有下面幾個。
 無上下文資訊的隱性反饋資料集 每一條行為記錄僅僅包含使用者ID和物品ID。
Book-Crossing（http://www2.informatik.uni-freiburg.de/~cziegler/BX/）就是這種型別的資料集。
 無上下文資訊的顯性反饋資料集 每一條記錄包含使用者ID、物品ID和使用者對物品的評分。
 有上下文資訊的隱性反饋資料集 每一條記錄包含使用者ID、物品ID和使用者對物品產生行為的時間戳。Lastfm資料集（

https://www.dtic.upf.edu/~ocelma/MusicRecommendationDataset/lastfm-1K.html）就是這種型別的資料集。
 有上下文資訊的顯性反饋資料集 每一條記錄包含使用者ID、物品ID、使用者對物品的評分和評分行為發生的時間戳。Netflix Prize（https://netflixprize.com/index.html）提供的就是這種型別的資料集。

2.2 使用者行為分析

2.2.1 使用者活躍度和物品流行度的分佈

令fu(k)為對k個物品產生過行為的使用者數，令fi(k)為被k個使用者產生過行為的物品數。那麼，fu(k)和fi(k)都滿足長尾分佈。

物品的流行度指對物品產生過行為的使用者總數。

使用者的活躍度為使用者產生過行為的物品總數。

不管是物品的流行度還是使用者的活躍度，都近似於長尾分佈。

2.2.2 使用者活躍度和物品流行度的關係

一般認為，新使用者傾向於瀏覽熱門的物品，因為他們對網站還不熟悉，只能點選首頁的熱門物品，而老使用者會逐漸開始瀏覽冷門的物品。

使用者越活躍，越傾向於瀏覽冷門的物品。

僅僅基於使用者行為資料設計的推薦演算法一般稱為協同過濾演算法。學術界對協同過濾演算法進行了深入研究，提出了很多方法，比如基於鄰域的方法（neighborhood-based）、隱語義模型（latent factor model）、基於圖的隨機遊走演算法（random walk on graph）等。在這些方法中，最著名的、在業界得到最廣泛應用的演算法是基於鄰域的方法，而基於鄰域的方法主要包含下面兩種演算法。

 基於使用者的協同過濾演算法：這種演算法給使用者推薦和他興趣相似的其他使用者喜歡的物品。

 基於物品的協同過濾演算法：這種演算法給使用者推薦和他之前喜歡的物品相似的物品。

2.3 實驗設計和演算法評測

2.3.1 資料集

MovieLens資料集，https://grouplens.org/datasets/movielens/

2.3.2 實驗設計

協同過濾演算法的離線實驗一般如下設計。首先，將使用者行為資料集按照均勻分佈隨機分成M份（本章取M=8），挑選一份作為測試集，將剩下的M-1份作為訓練集。然後在訓練集上建立使用者興趣模型，並在測試集上對使用者行為進行預測，統計出相應的評測指標。為了保證評測指標並不是過擬合的結果，需要進行M次實驗，並且每次都使用不同的測試集。然後將M次實驗測出的評測指標的平均值作為最終的評測指標。

2.3.3 評測指標

對使用者u推薦N個物品（記為R(u)），令使用者u在測試集上喜歡的物品集合為T(u)，然後可以通過準確率/召回率評測推薦演算法的精度：

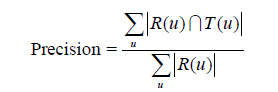
召回率描述有多少比例的使用者—物品評分記錄包含在最終的推薦列表中，而準確率描述最終的推薦列表中有多少比例是發生過的使用者—物品評分記錄。

覆蓋率反映了推薦演算法發掘長尾的能力，覆蓋率越高，說明推薦演算法越能夠將長尾中的物品推薦給使用者。

用推薦列表中物品的平均流行度度量推薦結果的新穎度。如果推薦出的物品都很熱門，說明推薦的新穎度較低，否則說明推薦結果比較新穎。

def Popularity(train, test, N):
    item_popularity = dict()
    for user, items in train.items():
        for item in items.keys()
            if item not in item_popularity:
                item_popularity[item] = 0
            item_popularity[item] += 1
    ret = 0
    n = 0
    for user in train.keys():
        rank = GetRecommendation(user, N)
        for item, pui in rank:
            ret += math.log(1 + item_popularity[item])
            n += 1
    ret /= n * 1.0
    return ret

2.4 基於鄰域的演算法

基於鄰域的演算法分為兩大類，一類是基於使用者的協同過濾演算法，另一類是基於物品的協同過濾演算法。

2.4.1 基於使用者的協同過濾演算法

1. 基礎演算法

在一個線上個性化推薦系統中，當一個使用者A需要個性化推薦時，可以先找到和他有相似興趣的其他使用者，然後把那些使用者喜歡的、而使用者A沒有聽說過的物品推薦給A。這種方法稱為基於使用者的協同過濾演算法。

基於使用者的協同過濾演算法主要包括兩個步驟。

(1) 找到和目標使用者興趣相似的使用者集合。

(2) 找到這個集合中的使用者喜歡的，且目標使用者沒有聽說過的物品推薦給目標使用者。

步驟(1)的關鍵就是計算兩個使用者的興趣相似度。這裡，協同過濾演算法主要利用行為的相似度計算興趣的相似度。

給定使用者u和使用者v，令N(u)表示使用者u曾經有過正反饋的物品集合，令N(v)為使用者v曾經有過正反饋的物品集合。那麼，我們可以通過如下的Jaccard公式簡單地計算u和v的興趣相似度：

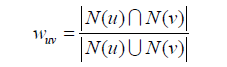
或者通過餘弦相似度計算：

以餘弦相似度為例，實現該相似度可以利用如下的偽碼：

def UserSimilarity(train):
    W = dict()
    for u in train.keys():
        for v in train.keys():
            if u == v:
                continue
            W[u][v] = len(train[u] & train[v])
            W[u][v] /= math.sqrt(len(train[u]) * len(train[v]) * 1.0)
    return W

這種方法的時間複雜度是O(|U|*|U|)，這在使用者數很大時非常耗時。我們可以首先計算出 $|N(u)\cap N(v)|\neq 0$ 的使用者對(u,v)，然後再對這種情況除以分母 $\sqrt{|N(u)||N(v))|}$ 。

為此，可以首先建立物品到使用者的倒排表，對於每個物品都儲存對該物品產生過行為的使用者列表。從而，可以掃描倒排表中每個物品對應的使用者列表，將使用者列表中的兩兩使用者對應的C[u][v]加1，最終就可以得到所有使用者之間不為0的C[u][v]。

def UserSimilarity(train):
    # build inverse table for item_users
    item_users = dict()
    for u, items in train.items():
        for i in items.keys():
            if i not in item_users:
                item_users[i] = set()
            item_users[i].add(u)
    #calculate co-rated items between users
    C = dict()
    N = dict()
    for i, users in item_users.items():
        for u in users:
            N[u] += 1
            for v in users:
                if u == v:
                    continue
                C[u][v] += 1
    #calculate finial similarity matrix W
    W = dict()
    for u, related_users in C.items():
        for v, cuv in related_users.items():
            W[u][v] = cuv / math.sqrt(N[u] * N[v])
    return W

得到使用者之間的興趣相似度後，UserCF演算法會給使用者推薦和他興趣最相似的K個使用者喜歡的物品。如下的公式度量了UserCF演算法中使用者u對物品i的感興趣程度：

def Recommend(user, train, W):
    rank = dict()
    interacted_items = train[user]
    for v, wuv in sorted(W[u].items, key=itemgetter(1), reverse=True)[0:K]:
        for i, rvi in train[v].items:
            if i in interacted_items:
                #we should filter items user interacted before
                continue
            rank[i] += wuv * rvi
    return rank

引數K是UserCF的一個重要引數，它的調整對推薦演算法的各種指標都會產生一定的影響。

（1）準確率和召回率，推薦系統的精度指標（準確率和召回率）並不和引數K成線性關係。

（2）流行度，K越大則UserCF推薦結果就越熱門。

（3）覆蓋率，K越大則UserCF推薦結果的覆蓋率越低。

2. 使用者相似度計算的改進

兩個使用者對冷門物品採取過同樣的行為更能說明他們興趣的相似度。根據使用者行為計算使用者的興趣相似度：

懲罰了使用者u和使用者v共同興趣列表中熱門物品對他們相似度的影響。稱為User-IIF演算法。

def UserSimilarity(train):
    # build inverse table for item_users
    item_users = dict()
    for u, items in train.items():
        for i in items.keys():
            if i not in item_users:
                item_users[i] = set()
            item_users[i].add(u)
    #calculate co-rated items between users
    C = dict()
    N = dict()
    for i, users in item_users.items():
        for u in users:
            N[u] += 1
            for v in users:
                if u == v:
                    continue
                C[u][v] += 1 / math.log(1 + len(users))
    #calculate finial similarity matrix W
    W = dict()
    for u, related_users in C.items():
        for v, cuv in related_users.items():
            W[u][v] = cuv / math.sqrt(N[u] * N[v])
    return W

UserCF-IIF在各項效能上略優於UserCF。這說明在計算使用者興趣相似度時考慮物品的流行度對提升推薦結果的質量確實有幫助。

3. 實際線上系統使用UserCF的例子

UserCF在目前的實際應用中使用並不多。其中最著名的使用者是Digg。

2.4.2 基於物品的協同過濾演算法

1. 基礎演算法

基於使用者的協同過濾演算法的缺點：

（1）隨著網站的使用者數目越來越大，計算使用者興趣相似度矩陣將越來越困難，其運算時間複雜度和空間複雜度的增長和使用者數的增長近似於平方關係。

（2）基於使用者的協同過濾很難對推薦結果作出解釋。

基於物品的協同過濾演算法（簡稱ItemCF）給使用者推薦那些和他們之前喜歡的物品相似的物品。ItemCF演算法並不利用物品的內容屬性計算物品之間的相似度，它主要通過分析使用者的行為記錄計算物品之間的相似度。該演算法認為，物品A和物品B具有很大的相似度是因為喜歡物品A的使用者大都也喜歡物品B。

基於物品的協同過濾演算法可以利用使用者的歷史行為給推薦結果提供推薦解釋。

基於物品的協同過濾演算法主要分為兩步。

(1) 計算物品之間的相似度。

(2) 根據物品的相似度和使用者的歷史行為給使用者生成推薦列表。

為了避免推薦出熱門的物品，可以用下面的公式計算物品的相似度：

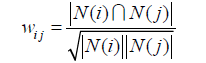
在協同過濾中兩個物品產生相似度是因為它們共同被很多使用者喜歡，也就是說每個使用者都可以通過他們的歷史興趣列表給物品“貢獻”相似度。

和UserCF演算法類似，用ItemCF演算法計算物品相似度時也可以首先建立使用者—物品倒排表（即對每個使用者建立一個包含他喜歡的物品的列表），然後對於每個使用者，將他物品列表中的物品兩兩在共現矩陣C中加1。

def ItemSimilarity(train):
    #calculate co-rated users between items
    C = dict()
    N = dict()
    for u, items in train.items():
        for i in users:
            N[i] += 1
            for j in users:
                if i == j:
                    continue
                C[i][j] += 1
    #calculate finial similarity matrix W
    W = dict()
    for i,related_items in C.items():
        for j, cij in related_items.items():
            W[u][v] = cij / math.sqrt(N[i] * N[j])
    return W

在得到物品之間的相似度後，ItemCF通過如下公式計算使用者u對一個物品j的興趣：

和使用者歷史上感興趣的物品越相似的物品，越有可能在使用者的推薦列表中獲得比較高的排名。

def Recommendation(train, user_id, W, K):
    rank = dict()
    ru = train[user_id]
    for i,pi in ru.items():
        for j, wj in sorted(W[i].items(), key=itemgetter(1), reverse=True)[0:K]:
            if j in ru:
                continue
            rank[j] += pi * wj
    return rank

ItemCF的一個優勢就是可以提供推薦解釋，即利用使用者歷史上喜歡的物品為現在的推薦結果進行解釋。

ItemCF演算法在不同K值下的效能：

（1）精度（準確率和召回率）：ItemCF推薦結果的精度也是不和K成正相關或者負相關的，因此選擇合適的K對獲得最高精度是非常重要的。
（2）流行度：和UserCF不同，引數K對ItemCF推薦結果流行度的影響也不是完全正相關的。隨著K的增加，結果流行度會逐漸提高，但當K增加到一定程度，流行度就不會再有明顯變化。
（3）覆蓋率：K增加會降低系統的覆蓋率。

2. 使用者活躍度對物品相似度的影響

活躍使用者對物品相似度的貢獻應該小於不活躍的使用者，他提出應該增加IUF引數（Inverse User Frequence，使用者活躍度對數的倒數）來修正物品相似度的計算公式：

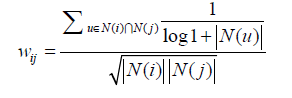演算法記為ItemCF-IUF。

def ItemSimilarity(train):
    #calculate co-rated users between items
    C = dict()
    N = dict()
    for u, items in train.items():
        for i in users:
            N[i] += 1
            for j in users:
                if i == j:
                    continue
                C[i][j] += 1 / math.log(1 + len(items) * 1.0)
    #calculate finial similarity matrix W
    W = dict()
    for i,related_items in C.items():
        for j, cij in related_items.items():
            W[u][v] = cij / math.sqrt(N[i] * N[j])
    return W

3. 物品相似度的歸一化

在研究中發現如果將ItemCF的相似度矩陣按最大值歸一化，可以提高推薦的準確率。

其實，歸一化的好處不僅僅在於增加推薦的準確度，它還可以提高推薦的覆蓋率和多樣性。

一般來說，熱門的類其類內物品相似度一般比較大。如果不進行歸一化，就會推薦比較熱門的類裡面的物品，而這些物品也是比較熱門的。因此，推薦的覆蓋率就比較低。相反，如果進行相似度的歸一化，則可以提高推薦系統的覆蓋率。

2.4.3 UserCF和ItemCF的綜合比較

UserCF的推薦更社會化，反映了使用者所在的小型興趣群體中物品的熱門程度，而ItemCF的推薦更加個性化，反映了使用者自己的興趣傳承。

UserCF適合用於新聞推薦，在圖書、電子商務和電影網站，比如亞馬遜、豆瓣、Netflix中，ItemCF則能極大地發揮優勢。

從技術上考慮，UserCF需要維護一個使用者相似度的矩陣，而ItemCF需要維護一個物品相似度矩陣。從儲存的角度說，如果使用者很多，那麼維護使用者興趣相似度矩陣需要很大的空間，同理，如果物品很多，那麼維護物品相似度矩陣代價較大。

哈利波特問題

很多書都和《哈利波特》相關，因為《哈利波特》太熱門了。

哈利波特問題有幾種解決方案。

（1）在分母上加大對熱門物品的懲罰

其中 $\alpha \in$ [0.5 ,1]。通過提高α，就可以懲罰熱門的j。

通過這種方法可以在適當犧牲準確率和召回率的情況下顯著提升結果的覆蓋率和新穎性（降低流行度即提高了新穎性）。

（2）引入物品的內容資料

2.5 隱語義模型

2.5.1 基礎演算法

隱語義模型（LFM，latent factor model）的核心思想是通過隱含特徵(latent factor)聯絡使用者興趣和物品。

對於某個使用者，首先得到他的興趣分類，然後從分類中挑選他可能喜歡的物品。

總結一下，這個基於興趣分類的方法大概需要解決3個問題。

（1）如何給物品進行分類？

（2）如何確定使用者對哪些類的物品感興趣，以及感興趣的程度？

（3）對於一個給定的類，選擇哪些屬於這個類的物品推薦給使用者，以及如何確定這些物品在一個類中的權重？

對於第一個問題：如何給物品進行分類？

簡單解決方案是找編輯給物品分類，編輯給出的分類仍然具有以下缺點：

a、編輯的意見不能代表各種使用者的意見。

b、編輯很難控制分類的粒度。

c、編輯很難給一個物品多個分類。

d、編輯很難給出多維度的分類。

e、編輯很難決定一個物品在某一個分類中的權重。

研究人員提出：為什麼我們不從資料出發，自動地找到那些類，然後進行個性化推薦？於是，隱含語義分析技術（latent variable analysis）出現了。隱含語義分析技術因為採取基於使用者行為統計的自動聚類，較好地解決了上面提出的5個問題。

a、編輯的意見不能代表各種使用者的意見，但隱含語義分析技術的分類來自對使用者行為的統計，代表了使用者對物品分類的看法。隱含語義分析技術和ItemCF在物品分類方面的思想類似，如果兩個物品被很多使用者同時喜歡，那麼這兩個物品就很有可能屬於同一個類。
b、編輯很難控制分類的粒度，但隱含語義分析技術允許我們指定最終有多少個分類，這個數字越大，分類的粒度就會越細，反正分類粒度就越粗。
c、編輯很難給一個物品多個分類，但隱含語義分析技術會計算出物品屬於每個類的權重，因此每個物品都不是硬性地被分到某一個類中。
d、編輯很難給出多維度的分類，但隱含語義分析技術給出的每個分類都不是同一個維度的，它是基於使用者的共同興趣計算出來的，如果使用者的共同興趣是某一個維度，那麼LFM給出的類也是相同的維度。
e、編輯很難決定一個物品在某一個分類中的權重，但隱含語義分析技術可以通過統計使用者行為決定物品在每個類中的權重，如果喜歡某個類的使用者都會喜歡某個物品，那麼這個物品在這個類中的權重就可能比較高。

相關方法：pLSA、LDA、隱含類別模型（latent class model）、隱含主題模型（latent topic model）、矩陣分解（matrix factorization

LFM通過如下公式計算使用者u對物品i的興趣：

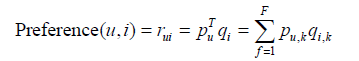
這個公式中pu,k 和qi,k 是模型的引數，其中pu,k 度量了使用者u的興趣和第k個隱類的關係，而qi,k 度量了第k個隱類和物品i之間的關係。

在隱性反饋資料集上應用LFM解決TopN推薦的第一個關鍵問題就是如何給每個使用者生成負樣本。

對負樣本取樣時應該遵循以下原則。

（1）對每個使用者，要保證正負樣本的平衡（數目相似）。

（2）對每個使用者取樣負樣本時，要選取那些很熱門，而使用者卻沒有行為的物品。

很熱門而使用者卻沒有行為更加代表使用者對這個物品不感興趣。因為對於冷門的物品，使用者可能是壓根沒在網站中發現這個物品，所以談不上是否感興趣。

def RandomSelectNegativeSample(self, items):
    ret = dict()
    for i in items.keys():
        ret[i] = 1
    n = 0
    for i in range(0, len(items) * 3):
        item = items_pool[random.randint(0, len(items_pool) - 1)]
        if item in ret:
            continue
        ret[item] = 0
        n + = 1
        if n > len(items):
            break
    return ret

取樣後，需要優化如下的損失函式來找到最合適的引數p和q：

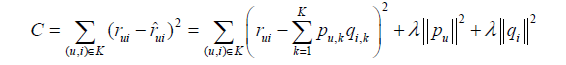
要最小化上面的損失函式，可以利用一種稱為隨機梯度下降法①的演算法。該演算法是最優化理論裡最基礎的優化演算法，它首先通過求引數的偏導數找到最速下降方向，然後通過迭代法不斷地優化引數。

$\frac{\partial C}{\partial p_{uk}} = -2q_{ik}*e_{ui} + 2\lambda p_{uk}$

$\frac{\partial C}{\partial q_{ik}} = -2p_{uk}*e_{ui}+ 2\lambda q_{ik}$

其中， $e_{ui} = r_{ui}-\sum_{k=1}^{K}p_{uk}q_{ik}$

根據隨機梯度下降法，需要將引數沿著最速下降方向向前推進，因此可以得到如下遞推公式：

$p_{uk} = p_{uk} + \alpha (q_{ik}*e_{ui} - \lambda p_{uk})$

$q_{ik} = q_{ik} + \alpha (p_{uk}*e_{ui} - \lambda q_{ik})$

其中，α是學習速率（learning rate），它的選取需要通過反覆實驗獲得。

def LatentFactorModel(user_items, F, N, alpha, lambda):
    [P, Q] = InitModel(user_items, F)
    for step in range(0,N):
        for user, items in user_items.items():
            samples = RandSelectNegativeSamples(items)
            for item, rui in samples.items():
                eui = rui - Predict(user, item)
                for f in range(0, F):
                    P[user][f] += alpha * (eui * Q[item][f] - lambda * P[user][f])
                    Q[item][f] += alpha * (eui * P[user][f] - lambda * Q[item][f])
                    alpha *= 0.9
def Recommend(user, P, Q):
    rank = dict()
    for f, puf in P[user].items():
        for i, qfi in Q[f].items():
            if i not in rank:
                rank[i] += puf * qfi
    return rank

在LFM中，重要的引數有4個：
 隱特徵的個數F；
 學習速率alpha；
 正則化引數lambda；
 負樣本/正樣本比例 ratio。
通過實驗發現，ratio引數對LFM的效能影響最大。隨著負樣本數目的增加，LFM的準確率和召回率有明顯提高。不過當ratio>10以後，準確率和召回率基本就比較穩定了。同時，隨著負樣本數目的增加，覆蓋率不斷降低，而推薦結果的流行度不斷增加，說明ratio引數控制了推薦演算法發掘長尾的能力。

2.5.2 基於LFM的實際系統的例子

雅虎的研究人員利用前文提到的LFM預測使用者是否會單擊連結:

LFM模型在實際使用中有一個困難，那就是它很難實現實時的推薦。經典的LFM模型每次訓練時都需要掃描所有的使用者行為記錄，這樣才能計算出使用者隱類向量（pu）和物品隱類向量（qi）。而且LFM的訓練需要在使用者行為記錄上反覆迭代才能獲得比較好的效能。因此，LFM的每次訓練都很耗時，一般在實際應用中只能每天訓練一次，並且計算出所有使用者的推薦結果。從而LFM模型不能因為使用者行為的變化實時地調整推薦結果來滿足使用者最近的行為。

為了解決傳統LFM不能實時化，而產品需要實時性的矛盾，雅虎的研究人員提出了一個解決方案。他們的解決方案分為兩個部分。首先，他們利用新聞連結的內容屬性（關鍵詞、類別等）得到連結i的內容特徵向量yi。其次，他們會實時地收集使用者對連結的行為，並且用這些資料得到連結i的隱特徵向量qi。然後，他們會利用如下公式預測使用者u是否會單擊連結i：

其中，yi是根據物品的內容屬性直接生成的，xuk是使用者u對內容特徵k的興趣程度，使用者向量xu可以根據歷史行為記錄獲得，而且每天只需要計算一次。而pu、qi是根據實時拿到的使用者最近幾小時的行為訓練LFM獲得的。

2.5.3 LFM和基於鄰域的方法的比較

	LFM	基於鄰域的方法
理論基礎	具有比較好的理論基礎，它是一種學習方法，通過優化一個設定的指標建立最優的模型。	更多的是一種基於統計的方法，並沒有學習過程
離線計算的空間複雜度	如果是F個隱類，那麼它需要的儲存空間是O(F*(M+N))，這在M和N很大時可以很好地節省離線計算的記憶體。	基於鄰域的方法需要維護一張離線的相關表。在離線計算相關表的過程中，如果使用者/物品數很多，將會佔據很大的記憶體。假設有M個使用者和N個物品，那麼假設是使用者相關表，則需要O(MM)的空間，而對於物品相關表，則需要O(NN)的空間。
離線計算的時間複雜度	如果用F個隱類，迭代S次，那麼它的計算複雜度是O(K * F * S)	假設有M個使用者、N個物品、K條使用者對物品的行為記錄。那麼，UserCF計算使用者相關表的時間複雜度是O(N * (K/N)^2)，而ItemCF計算物品相關表的時間複雜度是O(M*(K/M)^2)
線上實時推薦	可以線上進行實時的預測	不能進行線上實時推薦
推薦解釋	支援很好的推薦解釋	無法提供解釋

2.6 基於圖的模型

2.6.1 使用者行為資料的二分圖表示

使用者行為資料是由一系列二元組組成的，其中每個二元組(u, i)表示使用者u對物品i產生過行為。這種資料集很容易用一個二分圖①表示。

2.6.2 基於圖的推薦演算法

如果將個性化推薦演算法放到二分圖模型上，那麼給使用者u推薦物品的任務就可以轉化為度量使用者頂點vu和與vu沒有邊直接相連的物品節點在圖上的相關性，相關性越高的物品在推薦列表中的權重就越高。

圖中頂點的相關性主要取決於下面3個因素：

（1）兩個頂點之間的路徑數；

（2）兩個頂點之間路徑的長度；

（3）兩個頂點之間的路徑經過的頂點。

相關性高的一對頂點一般具有如下特徵：

（1）兩個頂點之間有很多路徑相連；

（2）連線兩個頂點之間的路徑長度都比較短；

（3）連線兩個頂點之間的路徑不會經過出度比較大的頂點。

基於隨機遊走的PersonalRank演算法

假設要給使用者u進行個性化推薦，可以從使用者u對應的節點vu開始在使用者物品二分圖上進行隨機遊走。遊走到任何一個節點時，首先按照概率α決定是繼續遊走，還是停止這次遊走並從vu節點開始重新遊走。如果決定繼續遊走，那麼就從當前節點指向的節點中按照均勻分佈隨機選擇一個節點作為遊走下次經過的節點。這樣，經過很多次隨機遊走後，每個物品節點被訪問到的概率會收斂到一個數。最終的推薦列表中物品的權重就是物品節點的訪問概率。

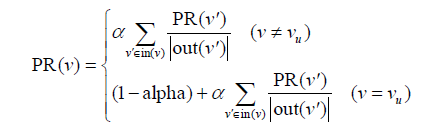
def PersonalRank(G, alpha, root):
    rank = dict()
    rank = {x:0 for x in G.keys()}
    rank[root] = 1
    for k in range(20):
        tmp = {x:0 for x in G.keys()}
        for i, ri in G.items():
            for j, wij in ri.items():
                if j not in tmp:
                    tmp[j] = 0
                tmp[j] += 0.6 * rank[i] / (1.0 * len(ri))
                if j == root:
                    tmp[j] += 1 - alpha
        rank = tmp
    return rank

雖然PersonalRank演算法可以通過隨機遊走進行比較好的理論解釋，但該演算法在時間複雜度上有明顯的缺點。因為在為每個使用者進行推薦時，都需要在整個使用者物品二分圖上進行迭代，直到整個圖上的每個頂點的PR值收斂。這一過程的時間複雜度非常高，不僅無法線上提供實時推薦，甚至離線生成推薦結果也很耗時。

解決PersonalRank時間複雜度很高的方案：（1）減少迭代次數，在收斂之前就停止。這樣會影響最終的精度，但一般來說影響不會特別大。（2）從矩陣論出發，重新設計演算法。

《推薦系統實踐》第二章 利用使用者行為資料