問題描述：要求將A柱子上的盤子移動到C柱子上，移動過程中大盤子不能在小盤子下邊(即必須滿足大盤在下，小盤在上)，求移動步驟？

示例：若A上只有1號和2號這2個盤子，移動步驟 A(2)-->>B,   A(1)-->>C ,  B(2)-->>C  【A(2)表示柱子A上的2號盤子】

思想：用遞迴(以3個盤子為例)

1、若只有1個盤子，直接將他從A柱子上移動到C柱子上；

2、若有n個盤子(假設n=3,即有3個盤子)，可以考慮先劃分為2個部分，構成大問題。即最下邊的1號盤子(部分1)和由2號和3號組成的整體(部分2, n-1個盤子)，先將部分2(藉助柱子C)移動到柱子B上，再將1號盤子(部分1)移動到柱子C上，最後將部分2(藉助柱子A)移動到柱子C上的1號盤子上邊，完成要求。

3、部分2的移動過程又是一個小問題，可以用遞迴。

程式碼示例：

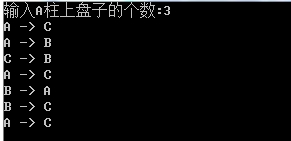
 1 #include <stdio.h>
 2 void hanoi(int n,char A,char B,char C){  //大問題
 3     if(n==1){
 4         printf("%c -> %c\n",A,C); //如果只有1個盤子直接移動
 5     }else{
 6         hanoi(n-1,A,C,B);  // 部分2率先移動從A移動到B(C是過渡) ，  分解成小問題
 7         printf("%c -> %c\n",A,C);//部分1 移動
 

 8         hanoi(n-1,B,A,C);  //部分2 從B移動到C (A是過渡)
 9     }
10 }
11 
12 
13 int main()
14 {
15     int  n ;
16     printf( "輸入A柱上盤子的個數:") ;
17     scanf("%d",&n) ;
18     hanoi(n,'A','B','C');
19 
20     return 0;
21 }

結果示例：