匯入標頭檔案

import matplotlib.pyplot as plt
from pylab import mpl
import numpy as np
import pandas as pd
import math
%matplotlib inline

得到差商表函式

def get_diff_table(X,Y):
    """
    得到插商表
    """
    n=len(X)
    A=np.zeros([n,n])
    
    for i in range(0,n):
        A[i][0] = Y[i]
    
    for j in range(1,n):
        for i in range(j,n):
            A[i][j] = (A[i][j-1] - A[i-1][j-1])/(X[i]-X[i-j])
    
    return A
 

計算插值函式

以下函式只是計算一個點的插值，還可以優化，因為計算一個區間上的點時，每次都要計算一次差商表

def newton_interpolation(X,Y,x):
    """
    計算x點的插值
    """
    sum=Y[0]
    temp=np.zeros((len(X),len(X)))
    #將第一行賦值
    for i in range(0,len(X)):
        temp[i,0]=Y[i]
    temp_sum=1.0
    for i in range(1,len(X)):
        #x的多項式
        temp_sum=temp_sum*(x-X[i-1])
        #計算均差
        for j in range(i,len(X)):
            temp[j,i]=(temp[j,i-1]-temp[j-1,i-1])/(X[j]-X[j-i])
        sum+=temp_sum*temp[i,i] 
    return sum
 

 得到插值表

X=[-1,0,1,2,3,4,5]
Y=[-20,-12,1,15,4,21,41]
A = get_diff_table(X,Y)
df = pd.DataFrame(A)
df

計算插值點的值並畫圖

xs=np.linspace(np.min(X),np.max(X),1000,endpoint=True)
ys=[]
for x in xs:
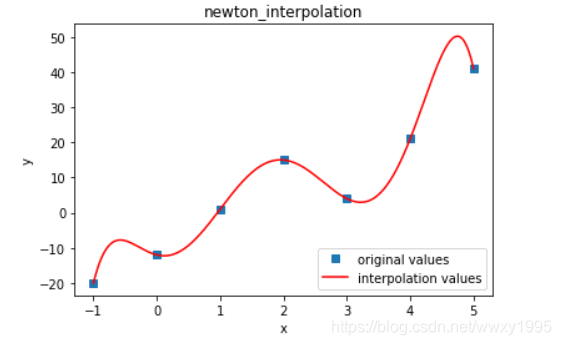
    ys.append(newton_interpolation(X,Y,x))

plt.title("newton_interpolation")
plt.plot(X,Y,'s',label="original values")#藍點表示原來的值
plt.plot(xs,ys,'r',label='interpolation values')#插值曲線
plt.xlabel('x')  
plt.ylabel('y')  
plt.legend(loc=4)#指定legend的位置右下角