以下是我的學習筆記，以及總結，如有錯誤之處請不吝賜教。

本文主要介紹聚類以及K均值演算法的推倒過程，最後有相關程式碼案例。

說到聚類就不得不先說說機器學習的分類。

機器學習主要分為三類：

監督學習：分類、迴歸...

無監督學習：聚類、降維...

強化學習。

下面這張圖是機器學習python庫sklearn的一個分類：

聚類的作用主要分為三個：

1. 組織資料
2. 降維
3. 資料預處理，為下部資料的處理做準備

聚類的應用主要包括：

• 網頁搜尋
• 生物技術
• 社交網路（如facebook、twitter等等）
• 商品推薦系統（劃重點）
• 天文
• 等等

輸入：兩個點之間的距離d（x）

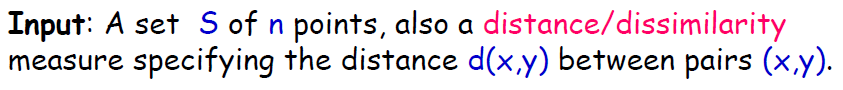
輸出：資料類別歸屬

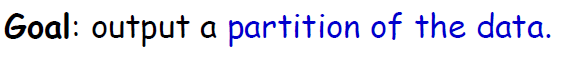
聚類基本的三類演算法：

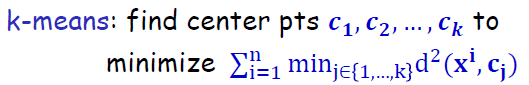
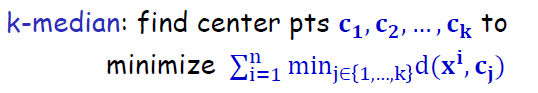
下面重點說K-means。

目標函式：最小化點到中心點的距離平方。公式如下：

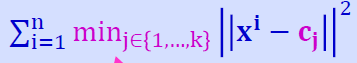
時間複雜度：屬於NP hard（在非確定圖靈機上無法解決（量子計算機））

先看幾個特例：

• K=1時的演算法：

• d=1時：需要用到動態規劃來計算。

K-means實現常用的幾種演算法：

• 通用的The Lloyd‘s演算法，即通過兩個迭代迴圈，第一層迴圈：求得到中心點的距離最近的點，第二層迴圈：求點到中心點的均值，不斷迴圈迭代。

    但是對於這種演算法，初始點的選擇是需要重點考慮的，初始化的方法主要有以下幾點：

•     隨機初始化，即隨機挑選點：

最後聚類得到：

但是容易遇到這種問題：

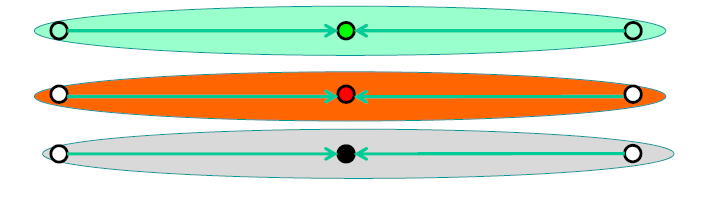
我們假設資料分佈是隨機獨立分佈，那麼所有資料被分到正確的類的概率為：,約等於：，概率隨著k的增大呈指數級別減小。

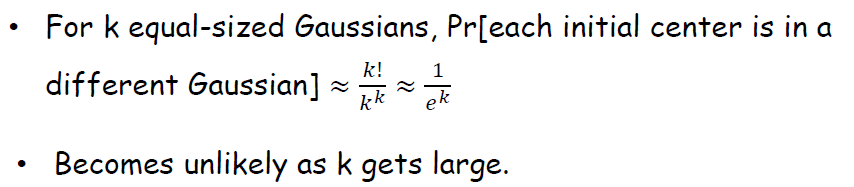
• 最遠點初始化，即找到距離前一個點最遠點作為初始化點：

但是最遠點也有問題：

• D2sampling：是目前最好的初始化方法，即加權重的最遠點
  ，也就是常說的K-means++，這個方法既可以保證隨機初始化無法找到所有類的問題，又可以避免最遠點的問題。具體的公式如下：

最關鍵的是，這個演算法的時間複雜度並沒有增加為：線性O(nkd），其中n為資料點個數，k為聚類中心點個數，d為資料集的維度。即初始化的複雜度可以忽略。

下面說說如何選擇k值：

• cross_validation  將資料集分為訓練集和測試集，選擇在訓練集效果最好的k值即可。
• elbow's method  找到k值下降斜率的拐點。

• 層次聚類，是聚類的另一個方法，他的不同類別有不同層次，類似於樹狀。他主要分為以下兩類：

1. 自上而下
2. 自下而上

自下而上有三種計算兩個類距離的方法：

1. single linkage
2. complete linkage
3. average linkage

這個演算法的時間複雜度較高，為：O（n3），當然通過優先佇列的資料結構可以降到O(n2logn）。

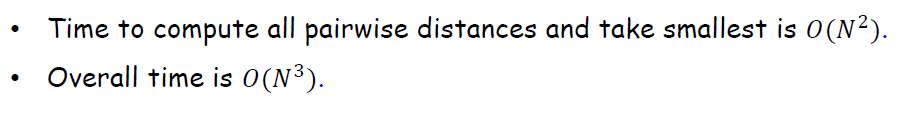
最重點的來了，K-means程式碼實現如下：

import os, sys
import argparse
import numpy as np
import time

# Vanilla K-means clustering.
samples = np.vstack([samples1, samples2, samples3])
rorder = np.arange(num_pts * 3)
rorder = np.random.shuffle(rorder)
samples = samples[rorder, :].squeeze()
# Lloyd's algorithm, with random initialization.
k = 3
centers = np.random.rand(k, 2)
num_iters = 10
losses = []
# Save for repeated use.
xdist = np.sum(samples * samples, axis=1)
for _ in xrange(num_iters):
    # Compute distance to each center.
    cdist = np.sum(centers * centers, axis=1) 
    consts = xdist[:, np.newaxis] + cdist
    dists = consts - 2 * np.dot(samples, centers.T)  #計算到中心點距離
    # Compute cluster assignment.
    ids = np.argmin(dists, axis=1)  #新的中心點迭代
    losses.append(np.sum(np.min(dists, axis=1)))
    for i in xrange(k):
        centers[i, :] = np.mean(samples[ids == i], axis=0)

具體可以看這裡：歡迎關注我的github

未完，待續。