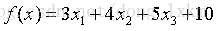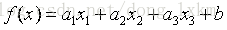梯度下降法求多元線性迴歸及Java實現
對於資料分析而言,我們總是極力找數學模型來描述資料發生的規律, 有的資料我們在二維空間就可以描述,有的資料則需要對映到更高維的空間。資料表現出來的分佈可能是完全離散的,也可能是聚整合堆的,那麼機器學習的任務就是讓計算機自己在資料中學習到資料的規律。那麼這個規律通常是可以用一些函式來描述,函式可能是線性的,也可能是非線性的,怎麼找到這些函式,是機器學習的首要問題。
本篇部落格嘗試用梯度下降法,找到線性函式的引數,來擬合一個數據集。
假設我們有如下函式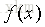
寫一個java程式來,隨機產生100筆資料作為訓練集。
Random random = new Random(); double[] results = new double[100]; double[][] features = new double[100][3]; for (int i = 0; i < 100; i++) { for (int j = 0; j < features[i].length; j++) { features[i][j] = random.nextDouble(); } results[i] = 3 * features[i][0] + 4 * features[i][1] + 5 * features[i][2] + 10; }
上面的程式中results就是函式的值,features的第二維就是隨機產生的3個x。
有了訓練集,我們的任務就變成了如何求出3個各種的係數3、4、5,以及偏移量10,係數和偏移量可以取任意值,那麼我們就得到了一個函式集,任務轉化一下就變成了找出一個函式作用於訓練集之後,與真實值的誤差最小,如何評判誤差的大小呢?我們需要定義一個函式來評判,那麼給這個函式取一個名字,叫損失函式。這裡,損失函式定義為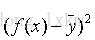
如何求這個函式的極小值呢?如果我們計算能力無限大,直接窮舉就完了,但是這不是高效的辦法,這時候就說的了梯度下降法,我們來看看數學裡對梯度的定義。
在微積分裡面,對多元函式的引數求∂偏導數,把求得的各個引數的偏導數以向量的形式寫出來,就是梯度。比如函式f(x,y), 分別對x,y求偏導數,求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,簡稱grad f(x,y)或者▽f(x,y)。
梯度告訴我們兩件事情:
1、函式增大的方向
2、我們走向增大的方向,應該走多大步幅
求極小值,我們反方向走即可,加個負號,但是這個步幅有個問題,如果過大,引數就直接飛出去了,就很難在找到最小值,如果太小,則很有可能卡在區域性極小值的地方。所以,我們設計了一個係數來調節步幅,我們叫它學習速率learningRate。
好了,為了好描述,我們把上面的函式泛化一下,表示成如下公式:
損失函式對每個引數求偏導數,根據偏導數值,當然求導的過程需要用到鏈式法則,,這裡我們直接給出引數更新公式如下:
對於BGD(批量梯度下降法):
對於SGD(隨機梯度下降法),SGD與BGD不同的是每筆資料,我們都更新一次引數,效率比較低下。公式和上面類似,去掉求和符號和除以N即可。
下面是具體的程式碼實現
import java.util.Random;
public class LinearRegression {
public static void main(String[] args) {
// y=3*x1+4*x2+5*x3+10
Random random = new Random();
double[] results = new double[100];
double[][] features = new double[100][3];
for (int i = 0; i < 100; i++) {
for (int j = 0; j < features[i].length; j++) {
features[i][j] = random.nextDouble();
}
results[i] = 3 * features[i][0] + 4 * features[i][1] + 5 * features[i][2] + 10;
}
double[] parameters = new double[] { 1.0, 1.0, 1.0, 1.0 };
double learningRate = 0.01;
for (int i = 0; i < 30; i++) {
SGD(features, results, learningRate, parameters);
}
parameters = new double[] { 1.0, 1.0, 1.0, 1.0 };
System.out.println("==========================");
for (int i = 0; i < 3000; i++) {
BGD(features, results, learningRate, parameters);
}
}
private static void SGD(double[][] features, double[] results, double learningRate, double[] parameters) {
for (int j = 0; j < results.length; j++) {
double gradient = (parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]) * features[j][0];
parameters[0] = parameters[0] - 2 * learningRate * gradient;
gradient = (parameters[0] * features[j][0] + parameters[1] * features[j][1] + parameters[2] * features[j][2]
+ parameters[3] - results[j]) * features[j][1];
parameters[1] = parameters[1] - 2 * learningRate * gradient;
gradient = (parameters[0] * features[j][0] + parameters[1] * features[j][1] + parameters[2] * features[j][2]
+ parameters[3] - results[j]) * features[j][2];
parameters[2] = parameters[2] - 2 * learningRate * gradient;
gradient = (parameters[0] * features[j][0] + parameters[1] * features[j][1] + parameters[2] * features[j][2]
+ parameters[3] - results[j]);
parameters[3] = parameters[3] - 2 * learningRate * gradient;
}
double totalLoss = 0;
for (int j = 0; j < results.length; j++) {
totalLoss = totalLoss + Math.pow((parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]), 2);
}
System.out.println(parameters[0] + " " + parameters[1] + " " + parameters[2] + " " + parameters[3]);
System.out.println("totalLoss:" + totalLoss);
}
private static void BGD(double[][] features, double[] results, double learningRate, double[] parameters) {
double sum = 0;
for (int j = 0; j < results.length; j++) {
sum = sum + (parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]) * features[j][0];
}
double updateValue = 2 * learningRate * sum / results.length;
parameters[0] = parameters[0] - updateValue;
sum = 0;
for (int j = 0; j < results.length; j++) {
sum = sum + (parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]) * features[j][1];
}
updateValue = 2 * learningRate * sum / results.length;
parameters[1] = parameters[1] - updateValue;
sum = 0;
for (int j = 0; j < results.length; j++) {
sum = sum + (parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]) * features[j][2];
}
updateValue = 2 * learningRate * sum / results.length;
parameters[2] = parameters[2] - updateValue;
sum = 0;
for (int j = 0; j < results.length; j++) {
sum = sum + (parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]);
}
updateValue = 2 * learningRate * sum / results.length;
parameters[3] = parameters[3] - updateValue;
double totalLoss = 0;
for (int j = 0; j < results.length; j++) {
totalLoss = totalLoss + Math.pow((parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]), 2);
}
System.out.println(parameters[0] + " " + parameters[1] + " " + parameters[2] + " " + parameters[3]);
System.out.println("totalLoss:" + totalLoss);
}
}執行結果如下:
同樣是更新3000次引數。
1、SGD結果:
引數分別為:3.087332784857909 、4.075233812033048 、5.06020828348889、 9.89116046652793
totalLoss:0.13515381461776949
2、BGD結果:
引數分別為:3.0819123489025344 、4.064145151461403、5.046862571520019、 9.899847277313173
totalLoss:0.1050937019067582
可以看出,BGD有更好的表現。
快樂源於分享。
此部落格乃作者原創, 轉載請註明出處