Time Limits: 1000 ms Memory Limits: 524288 KB

Description

C城將要舉辦一系列的賽車比賽。在比賽前，需要在城內修建m條賽道。
C城一共有n個路口，這些路口編號為1,2,…,n ，有n-1 條適合於修建賽道的雙向通行的道路，每條道路連線著兩個路口。其中，第i條道路連線的兩個路口編號為ai 和bi ，該道路的長度為li 。藉助這n-1 條道路，從任何一個路口出發都能到達其他所有的路口。
一條賽道是一組互不相同的道路e1,e2,…,ek ，滿足可以從某個路口出發，依次經過道路 e1,e2,…,ek（每條道路經過一次，不允許調頭）到達另一個路口。一條賽道的長度等於經過的各道路的長度之和。為保證安全，要求每條道路至多被一條賽道經過。
目前賽道修建的方案尚未確定。你的任務是設計一種賽道修建的方案，使得修建的m條賽道中長度最小的賽道長度最大（即m條賽道中最短賽道的長度儘可能大）。

Input

輸入檔名為track.in。
輸入檔案第一行包含兩個由空格分隔的正整數 n,m，分別表示路口數及需要修建的賽道數。
接下來n-1 行，第i行包含三個正整數ai,bi,li ，表示第i條適合於修建賽道的道路連線的兩個路口編號及道路長度。保證任意兩個路口均可通過這n-1條道路相互到達。每行中相鄰兩數之間均由一個空格分隔。

Output

輸出檔名為track.out。
輸出共一行，包含一個整數，表示長度最小的賽道長度的最大值。

Sample Input

輸入1：
7 1
1 2 10
1 3 5
2 4 9
2 5 8
3 6 6
3 7 7

輸入2：
9 3
1 2 6
2 3 3
3 4 5
4 5 10
6 2 4
7 2 9
8 4 7
9 4 4

Sample Output

輸出1：
31

輸出2：
15

Data Constraint

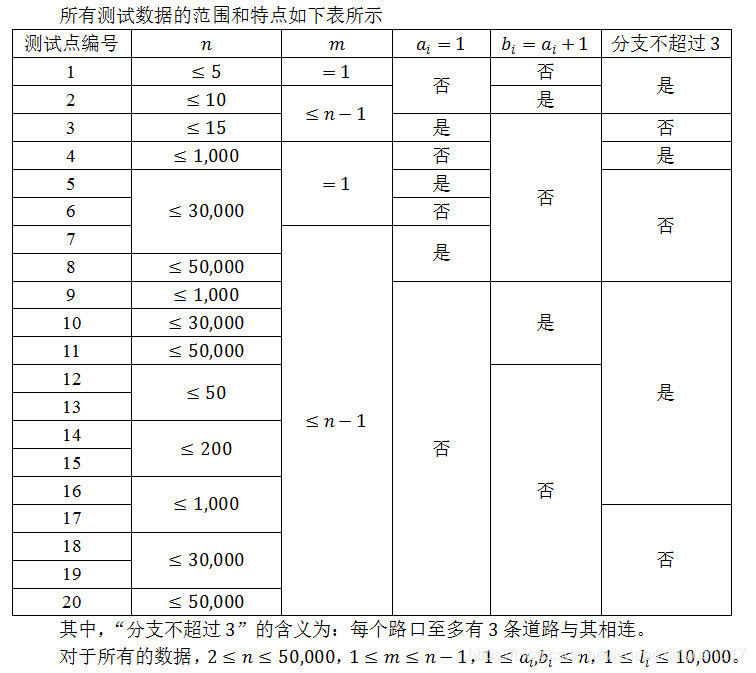
Hint

【輸入輸出樣例1說明】
所有路口及適合於修建賽道的道路如下圖所示：

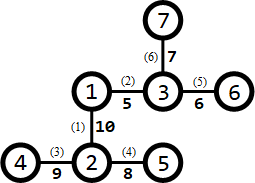
道路旁括號內的數字表示道路的編號，非括號內的數字表示道路長度。
需要修建1條賽道。可以修建經過第3,1,2,6條道路的賽道（從路口4到路口7），則該賽道的長度為9+10+5+7=31 ，為所有方案中的最大值。

【輸入輸出樣例2說明】
所有路口及適合於修建賽道的道路如下圖所示：

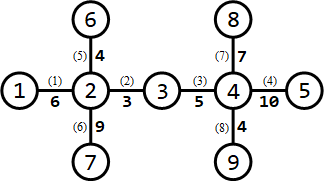
需要修建3條賽道。可以修建如下3條賽道：

1. 經過第1,6條道路的賽道（從路口1到路口7），長度為6+9=15 ；
2. 經過第5,2,3,8條道路的賽道（從路口6到路口9），長度為4+3+5+4=16 ；
3. 經過第7,4條道路的賽道（從路口8到路口5），長度為7+10=17。
   長度最小的賽道長度為15 ，為所有方案中的最大值。

Solution

最小長度最大，考慮二分+判定
考慮以 $x$ 為根的子樹，最優解中一部分鏈在子樹的內部，還有可能是一條經過 $x$ 往外延伸的鏈
可證明一定存在一個最優解使完全在子樹內部的鏈儘可能多，否則可以調整子樹內部的方案，不會使答案變差
如果有兩種方案使得子樹內部的鏈一樣多，我們肯定希望使剩下可以往上擴充套件的鏈儘可能長
$sum[x]$ 表示在 $x$ 子樹內合法的路徑最多有多少條， $mx[x]$ 表示 $x$ 子樹內在最多路徑情況下往外延伸的鏈的最大長度
考慮用這兩個值進行轉移
首先，若 $mx[x]>=mid$ 肯定是不划算的，因為可以直接切出一條鏈
其次，對於每個兒子 $y$ ，它提供 $l[y]=mx[y]+len(x,y)$ 的可拼接鏈長以及 $sum[y]$ 的貢獻
考慮對答案產生新貢獻的兩種情況
1. $l[y]>=mid$ 則 $sum[x]+1$
2. $l[y1]+l[y2]>=mid$ 的兩條鏈拼接起來形成答案， $sum[x]+1$
這裡的選擇可以用multiset維護，注意一下細節

Code

#pragma GCC optimize(2)
#pragma G++ optimize(2)

#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cctype>
#include<set>

#define fo(i,a,b) for(int i=a;i<=b;++i)
#define fd(i,a,b) for(int i=a;i>=b;--i)
#define ll long long

using namespace std;

const int N=5e4+5;
int n,m,num;
int a[N],mx[N],sum[N],last[N];
ll l=0,r=0,mid,ans=0;
struct edge{int to,next,l;}e[2*N];
multiset<int> S;
multiset<int>::iterator it,i1,i2;

inline void read(int &n)
{
	int x=0,w=0; char ch=0;
	while(!isdigit(ch)) w|=ch=='-',ch=getchar();
	while(isdigit(ch)) x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	n=w?-x:x;
}

void link(int x,int y,int z)
{
	e[++num]=(edge){y,last[x],z},last[x]=num;
}

void dfs(int x,int fa)
{
	for(int w=last[x];w;w=e[w].next)
	{
		int y=e[w].to;
		if(y==fa) continue;
		dfs(y,x);
	}
	S.clear();
	int tot=0,cnt=0;
	for(int w=last[x];w;w=e[w].next)
	{
		int y=e[w].to;
		if(y==fa) continue;
		tot+=sum[y];
		int len=mx[y]+e[w].l;
		if(len>=mid) {++tot; continue;}
		S.insert(len);
		a[++cnt]=len;
	}
	sort(a+1,a+1+cnt);
	fd(i,cnt,1)
	{
		i1=S.find(a[i]);
		if(i1==S.end()) break;
		i2=S.lower_bound(mid-a[i]);
		if(i2==S.end()) break;
		if(i1==i2)
		{
			++i2;
			if(i2==S.end()) break;
		}
		S.erase(i1),S.erase(i2),++tot;
	}
	int tmp=0;
	if(!S.empty()) it=S.end(),it--,tmp=*it;
	sum[x]=tot,mx[x]=tmp;
}

int check()
{
	memset(mx,0,sizeof(mx));
	memset(sum,0,sizeof(sum));
	dfs(1,0);
	if(sum[1]>=m) return 1;
	return 0;
}

int main()
{
	freopen("track.in","r",stdin);
	freopen("track.out","w",stdout);
	read(n),read(m);
	fo(i,1,n-1)
	{
		int x,y,z;
		read(x),read(y),read(z);
		link(x,y,z),link(y,x,z);
		r+=z;
	}
	while(l<=r)
	{
		mid=(l+r)>>1;
		if(check()) l=mid+1,ans=max(ans,mid);
			else r=mid-1;
	}
	printf("%d",ans);
}