三種啟用函式以及它們的優缺點
三種啟用函式以及它們的優缺點
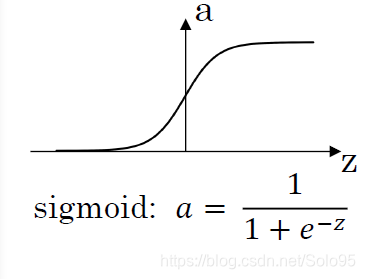
導數:
最基本的啟用函式,logistics regression以及講解深度神經網路的時候作為簡單例子,但實際上很少使用。
原因如下:
當z非常大或者非常小的時候,a的斜率變得越來越接近0,這會使得梯度下降演算法變得極為緩慢。
但 非常適合作為二元分類網路輸出層的啟用函式,因為在該應用場景下你需要 ,而不是 的
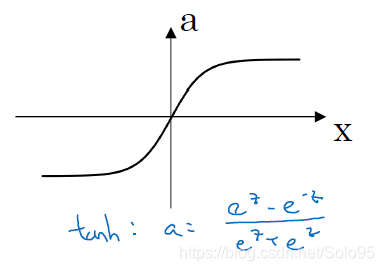
導數:
其實相當於把 平移到以原點為中心,然後再縮放到 的範圍。
使用 作為啟用函式在絕大多數情況下都比sigmoid要好得多,僅有上面提及的二元分類輸出層為例外。
而且使用tan(h)能夠中心化你的資料,中心化的含義是資料的均值接近0而不是像0.5這樣的值。這會使得下一層的學習變得簡單一點。
但是 和 一樣,在當z非常大或者非常小的時候,a的斜率變得越來越接近0,使得深度下降演算法變得極為緩慢。
ReLU(Rectified Linear Unit)
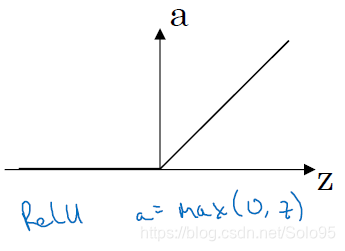
最最最常用的啟用函式。
導數:
它的唯一缺點可能就是有一半的範圍(圖左),a都是0。但實際使用中,足夠多的神經網路層數會使得a維持在 的範圍內,所以該缺點影響不大。
另外因為斜率在 時恆等於1,擺脫了前兩種啟用函式使得學習速率下降的問題,可以始終維持比較快的學習速度。一般來說,ReLU都比其他啟用函式學習得快一點。
這也是為什麼CNN乾脆把某些層命名為ReLU層,即線性整流層,博主會在CNN的博文裡提及除了加快學習速度的其他原因。
leaky ReLU
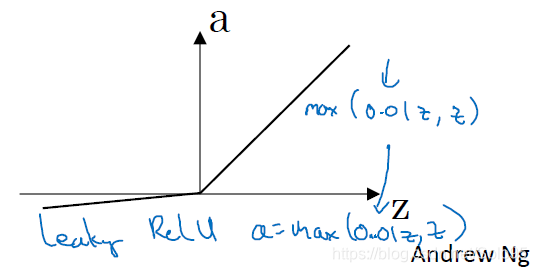
ReLU的一種變種,將ReLU中斜率為0的部分,變成了
,你可以調整0.01為其他值,看能否取得更好的效果。
導數:
一般來說。leaky ReLU能比ReLU取得更好的結果,但實際很少有人使用。
Summary
三種啟用函式都有一定的使用場景,ReLU的流行只是在大部分的場景下都適用,具體要選擇哪種啟用函式,要根據你自己的實際應用來作決策。如果你不確定你要用什麼,ReLU不會讓你失望。
在使用ReLU時,ReLU和leaky ReLU任取一個即可,也可以都嘗試一下,哪一個能取得最佳結果。
