(三)提升樹模型:Lightgbm原理深入探究
本篇部落格是提升樹模型部落格的第三篇文章,也是最後一篇文章。
第一篇介紹GBDT的部落格可以參看這裡。
第二篇介紹Xgboost的部落格可以參看這裡。
本篇部落格主要講解輕量級的提升樹模型-LightGBM。
LightGBM的資料網上也出現很多,但是講解的都很淺,大部分都是從官方文件摘抄過來的,沒有深究。我的能力也比較有限,無法深入體會作者的思路。對於LightGBM很多細節,我也是一知半解。
但是,我還是在參考部分資料和原始碼的基礎上,整理出了本文。供讀者參考,非常歡迎讀者留言討論,共同進步。
目錄
2.2.1 Leaf-wise (Best-first) 的決策樹生長策略
3.1 如果改變資料集的特徵的順序,為什麼訓練的結果卻不一樣?
3.2 在custom objective中Hessian的作用是什麼呢?
3. 3 scale_pos_weight引數實現的機制是什麼?
3.5 LGBM中,迴歸和二分類問題中的初始第0顆樹的預測值是什麼?
3.6 當我們訓練完模型後,測試集預測的值是怎麼樣基於訓練模型得到的?
一、前言
16年底,微軟DMTK(分散式機器學習工具包)團隊在GitHub上開源了效能超越其他boosting工具的LightGBM,在三天之內GitHub上被star了1000次,fork了200次,可見LightGBM的火爆程度。
在前面我們也說過,GBDT (Gradient Boosting Decision Tree)是機器學習中一個長盛不衰的模型,其主要思想是利用弱分類器(決策樹)迭代訓練以得到最優模型,該模型具有訓練效果好、不易過擬合等優點。GBDT在工業界應用廣泛,通常被用於點選率預測,搜尋排序等任務。GBDT也是各種資料探勘競賽的致命武器,據統計Kaggle上的比賽有一半以上的冠軍方案都是基於GBDT。Xgboost是GBDT的集大成者,但是LightGBM的出現挑戰了Xgboost在“江湖”上的地位,因此,本文接下來介紹LightGBM的內容,主要與Xgboost進行對比。
LightGBM (Light Gradient Boosting Machine)(官方github,英文官方文件,中文官方文件)是一個實現GBDT演算法的輕量級框架,支援高效率的並行訓練,並且具有以下優點:
-
更快的訓練效率
-
低記憶體使用
-
更高的準確率
-
支援並行化學習
-
可處理大規模資料
從LightGBM的GitHub主頁上可以直接看到與Xgboost的對比實驗結果:
訓練速度方面

記憶體消耗方面

準確率方面

從多個實驗資料可以看出,LightGBM在不損失學習精度的情況下,不僅比XGBoost快,且佔用記憶體低。
二、LightGBM優化
LightGBM實現了Xgboost的幾乎所有功能,除GPU支援,多種應用,多種度量方式外,還做了許多的優化。
2.1 速度和記憶體的優化
xgboost中預設的演算法對於決策樹的學習使用基於 pre-sorted 的演算法 [1, 2],這是一個簡單的解決方案,但是不易於優化。
LightGBM 利用基於 histogram 的演算法 [3, 4, 5],通過將連續特徵(屬性)值分段為 discrete bins 來加快訓練的速度並減少記憶體的使用。 如下的是基於 histogram 演算法的優點:
- 減少分割增益的計算量
- Pre-sorted 演算法需要
O(#data)次的計算。即計算最大分裂增益需要O(#data*#features) - Histogram 演算法只需要計算
O(#bins)次, 並且#bins遠少於#data。即計算最大分裂增益需要O(#bins*#features)
- Pre-sorted 演算法需要
- 通過直方圖的相減來進行進一步的加速
- 在二叉樹中可以通過利用葉節點的父節點和相鄰節點的直方圖的相減來獲得該葉節點的直方圖
- 所以僅僅需要為一個葉節點建立直方圖 (其
#data小於它的相鄰節點)就可以通過直方圖的相減來獲得相鄰節點的直方圖,而這花費的代價(O(#bins))很小。
- 減少記憶體的使用
- 可以將連續的值替換為 discrete bins。 如果
#bins較小, 可以利用較小的資料型別來儲存訓練資料, 如 uint8_t。 - 無需為 pre-sorting 特徵值儲存額外的資訊
- 可以將連續的值替換為 discrete bins。 如果
- 減少並行學習的通訊代價
綜上,直方圖演算法是LightGBM在速度和記憶體上優化的主要方法。關於LightGBM的直方圖演算法的詳細討論,可以參看我的另一篇部落格。
2.2 準確率的優化
2.2.1 Leaf-wise (Best-first) 的決策樹生長策略
大部分決策樹的學習演算法通過 level(depth)-wise 策略生長樹,如下圖一樣:

LightGBM 通過 leaf-wise (best-first)[6] 策略來生長樹。它將選取具有最大 delta loss 的葉節點來生長。 當生長相同的 #leaf,leaf-wise 演算法可以比 level-wise 演算法減少更多的損失。
當 #data 較小的時候,leaf-wise 可能會造成過擬合。 所以,LightGBM 可以利用額外的引數 max_depth 來限制樹的深度並避免過擬合(樹的生長仍然通過 leaf-wise 策略)。

2.2.2 類別特徵值的最優分割
我們通常將類別特徵轉化為 one-hot coding。 然而,對於學習樹來說這不是個好的解決方案。 原因是,對於一個基數較大的類別特徵,學習樹會生長的非常不平衡,並且需要非常深的深度才能來達到較好的準確率。
事實上,最好的解決方案是將類別特徵劃分為兩個子集,總共有 2^(k-1) - 1 種可能的劃分,k是這個類別特徵的可能取值個數。但是對於迴歸樹 [7] 有個有效的解決方案。為了尋找最優的劃分需要大約 k * log(k) .
基本的思想是根據訓練目標的相關性對類別進行重排序。 更具體的說,根據累加值(sum_gradient / sum_hessian)重新對(類別特徵的)直方圖進行排序,然後在排好序的直方圖中尋找最好的分割點。
關於LightGBM的類別特徵值的最優分割的詳細討論,可以參看我的另一篇部落格。
2.3 並行學習的優化
LightGBM 提供以下並行學習優化演算法:
2.3.1 特徵並行
傳統演算法
傳統的特徵並行演算法旨在於在並行化決策樹中的Find Best Split.主要流程如下:
- 垂直劃分資料(不同的機器有不同的特徵集)
- 在本地特徵集尋找最佳劃分點 {特徵, 閾值}
- 本地進行各個劃分的通訊整合並得到最佳劃分
- 以最佳劃分方法對資料進行劃分,並將資料劃分結果傳遞給其他執行緒
- 其他執行緒對接受到的資料進一步劃分
傳統的特徵並行方法主要不足:
- split finding計算複雜度高為O(#data),當資料量很大的時候,慢。
- 需要對劃分的結果進行通訊整合,其額外的時間複雜度約為 “O(#data/8)”(一個數據一個位元組)。

LightGBM 中的特徵並行
既然在資料量很大時,傳統資料並行方法無法有效地加速,我們做了一些改變:不再垂直劃分資料,即每個執行緒都持有全部資料。 因此,LightGBM中沒有資料劃分結果之間通訊的開銷,各個執行緒都知道如何劃分資料。 而且,“#data” 不會變得更大,所以,在使每天機器都持有全部資料是合理的。
LightGBM 中特徵並行的流程如下:
- 每個執行緒都在本地資料集上尋找最佳劃分點{特徵, 閾值}
- 本地進行各個劃分的通訊整合並得到最佳劃分
- 執行最佳劃分
然而,該特徵並行演算法在資料量很大時,每個機器儲存所有資料代價高。因此,建議在資料量很大時使用資料並行。
2.3.2 資料並行
傳統演算法
資料並行旨在於並行化整個決策學習過程。資料並行的主要流程如下:
- 水平劃分資料
- 執行緒以本地資料構建本地直方圖
- 將本地直方圖整合成全域性整合圖
- 在全域性直方圖中尋找最佳劃分,然後執行此劃分

傳統資料劃分的不足:
- 高通訊開銷。 如果使用點對點的通訊演算法,一個機器的通訊開銷大約為 “O(#machine * #feature * #bin)” 。 如果使用整合的通訊演算法(例如, “All Reduce”等),通訊開銷大約為 “O(2 * #feature * #bin)”[8] 。
LightGBM中的資料並行
LightGBM 中採用以下方法較少資料並行中的通訊開銷:
- 不同於“整合所有本地直方圖以形成全域性直方圖”的方式,LightGBM 使用分散規約(Reduce scatter)的方式,把直方圖合併的任務分攤到不同的機器,對不同機器的不同特徵(不重疊的)進行整合。 然後執行緒從本地整合直方圖中尋找最佳劃分並同步到全域性的最佳劃分中。
- LightGBM 通過直方圖做差法加速訓練。 基於此,我們可以進行單葉子的直方圖通訊,並且在相鄰直方圖上使用做差法。
通過上述方法,LightGBM 將資料並行中的通訊開銷減少到 “O(0.5 * #feature * #bin)”。
2.3.3 投票並行
投票並行未來將致力於將“資料並行”中的通訊開銷減少至常數級別。 其將會通過兩階段的投票過程較少特徵直方圖的通訊開銷 [9] .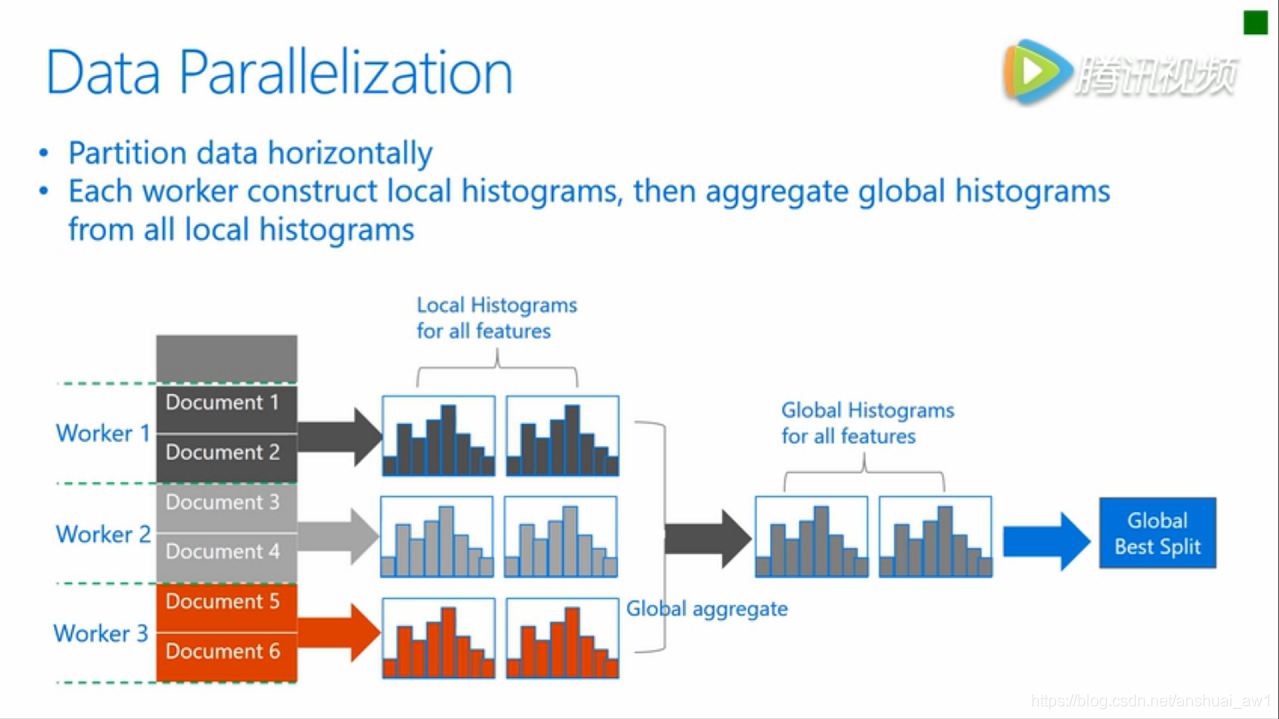
基於投票的並行是對資料並行的優化,資料並行的瓶頸主要在於合併直方圖的時候,通訊代價比較大。根據這一點,基於投票的並行,用投票的方式只合並部分特徵值的直方圖,達到了降低通訊量的目的。首先,通過本地的資料找到本地的top k best features. 然後利用投票篩選出可能是全域性最優分割點的特徵,合併直方圖的時候只合並這些被選出來的特徵,從此降低了通訊量。
三、細節Q&A
3.1 如果改變資料集的特徵的順序,為什麼訓練的結果卻不一樣?
也就是說,第一次訓練特徵的順序為[col1,col2.col3],第一次訓練特徵的順序為[col3,col1.col2],但是訓練的結果卻不一樣
A: 在LGBM中,當選擇一個特徵進行分裂時,如果2個特徵的增益相同,那麼就會選擇較小索引(smaller index(id))的特徵。
參考:https://github.com/Microsoft/LightGBM/issues/1294
3.2 在custom objective中Hessian的作用是什麼呢?
在LightGBM的論文中,分裂增益是計算的梯度的方差增益,那麼在custom objective中定義的Hessian的作用是什麼呢?
A:在論文3.2公式(1)中,可以看到分母都是樣本的個數,如果把樣本的個數換成Hessian,那麼就變成了Hessian最優了。
具體的增益公式需要從程式碼中讀,先留個坑。
參考:https://github.com/Microsoft/LightGBM/issues/1463
3. 3 scale_pos_weight引數實現的機制是什麼?
A:先看一下官方文件對scale_pos_weight的介紹:
預設值為1,只能在二分類中使用。
無論是在xgboost還是LightGBM, scale_pos_weight=1代表了正樣例和負樣例是完美地平衡:
number of positive samples = number of negative samples
scale_pos_weight的定義是:
sample_pos_weight = number of negative samples / number of positive samples
也就是負樣本的個數除以正樣本的個數。
換句話說,number of positive samples * sample_pos_weight = number of negative samples
Related C++ code:
-
xgboost proof:
w += y * ((param_.scale_pos_weight * w) - w);where y is the label (0 negative or 1 positive in src/objective/regression_obj.cc) -
LightGBM proof:
label_weights_[1] *= scale_pos_weight_;where the 2nd index (1) is for positive labels (in src/objective/binary_objective.hpp)
3.4 LGBM如何計算增益的?
A: 在xgb中,我們已經知道一個葉子的純度分數為:-sum_grad / (sum_hess + lamdba)
而在LGB中,lambda_l2其實就是lamdba,代表L2正則化的引數。
原始碼:https://github.com/Microsoft/LightGBM/blob/master/src/treelearner/feature_histogram.hpp#L291-L297
在原始碼450行:可以看到, LGBM的一個葉子的純度分數也為:-sum_grad / (sum_hess + lambda_l2)
static double CalculateSplittedLeafOutput(double sum_gradients, double sum_hessians, double l1, double l2, double max_delta_step) {
double ret = -ThresholdL1(sum_gradients, l1) / (sum_hessians + l2);
if (max_delta_step <= 0.0f || std::fabs(ret) <= max_delta_step) {
return ret;
} else {
return Common::Sign(ret) * max_delta_step;
}
}在原始碼461行:可以看到增益GetSplitGains是:GetLeafSplitGainGivenOutput(sum_left_gradients, sum_left_hessians, l1, l2, left_output) + GetLeafSplitGainGivenOutput(sum_right_gradients, sum_right_hessians, l1, l2, right_output)
static double GetSplitGains(double sum_left_gradients, double sum_left_hessians,
double sum_right_gradients, double sum_right_hessians,
double l1, double l2, double max_delta_step,
double min_constraint, double max_constraint, int8_t monotone_constraint) {
double left_output = CalculateSplittedLeafOutput(sum_left_gradients, sum_left_hessians, l1, l2, max_delta_step, min_constraint, max_constraint);
double right_output = CalculateSplittedLeafOutput(sum_right_gradients, sum_right_hessians, l1, l2, max_delta_step, min_constraint, max_constraint);
if (((monotone_constraint > 0) && (left_output > right_output)) ||
((monotone_constraint < 0) && (left_output < right_output))) {
return 0;
}
return GetLeafSplitGainGivenOutput(sum_left_gradients, sum_left_hessians, l1, l2, left_output)
+ GetLeafSplitGainGivenOutput(sum_right_gradients, sum_right_hessians, l1, l2, right_output);
}在原始碼503行,可以看到 GetLeafSplitGainGivenOutput
static double GetLeafSplitGainGivenOutput(double sum_gradients, double sum_hessians, double l1, double l2, double output) {
const double sg_l1 = ThresholdL1(sum_gradients, l1);
return -(2.0 * sg_l1 * output + (sum_hessians + l2) * output * output);
}我們這時候來推一下GetLeafSplitGainGivenOutput的結果-(2.0 * sg_l1 * output + (sum_hessians + l2) * output * output):
output就是;sg_l1可以認為是G。
代入約減後是:
GetSplitGains即為:
我疑惑的點是仍然與XGB中的增益不同:
有讀者知道的麻煩留言告訴我。
參考:https://github.com/Microsoft/LightGBM/issues/1283
3.5 LGBM中,迴歸和二分類問題中的初始第0顆樹的預測值是什麼?
A: 根據boost_from_average設定,使用所有標籤的均值作為第0顆樹的預測值。
3.6 當我們訓練完模型後,測試集預測的值是怎麼樣基於訓練模型得到的?
A: LGBM是類似於xgb的加法模型,在這篇文章裡已經講過了這是一個加法模型,即一個測試樣本在每顆樹的葉子節點的值相加就是最終預測的值。假如一共有3顆樹,測試樣本所在的3個樹的葉子節點直接相加就是預測值。
那麼,learning_rate的作用體現在了哪裡呢?在上述連結的例子裡就可以體現。也就是說,葉子節點的值已經乘過了learning_rate。
3.7 LGBM如何畫出決策樹?
A: 與xgb畫圖的過程是一樣的,參考連結。只是plot_tree的引數不一樣。其餘都是一樣的。
# 獲取測試集落在樹模型的哪個葉子節點上
y_leaf_index = gbm.predict(X_test, pred_leaf = True)
# 畫出最後一棵樹
lgb.plot_tree(gbm, tree_index=gbm.best_iteration_-1)參考文獻:
[1] Mehta, Manish, Rakesh Agrawal, and Jorma Rissanen. “SLIQ: A fast scalable classifier for data mining.” International Conference on Extending Database Technology. Springer Berlin Heidelberg, 1996.
[2] Shafer, John, Rakesh Agrawal, and Manish Mehta. “SPRINT: A scalable parallel classifier for data mining.” Proc. 1996 Int. Conf. Very Large Data Bases. 1996.
[3] Ranka, Sanjay, and V. Singh. “CLOUDS: A decision tree classifier for large datasets.” Proceedings of the 4th Knowledge Discovery and Data Mining Conference. 1998.
[4] Machado, F. P. “Communication and memory efficient parallel decision tree construction.” (2003).
[5] Li, Ping, Qiang Wu, and Christopher J. Burges. “Mcrank: Learning to rank using multiple classification and gradient boosting.” Advances in neural information processing systems. 2007.
[6] Shi, Haijian. “Best-first decision tree learning.” Diss. The University of Waikato, 2007.
[7] Walter D. Fisher. “On Grouping for Maximum Homogeneity.” Journal of the American Statistical Association. Vol. 53, No. 284 (Dec., 1958), pp. 789-798.
[8] Thakur, Rajeev, Rolf Rabenseifner, and William Gropp. “Optimization of collective communication operations in MPICH.” International Journal of High Performance Computing Applications 19.1 (2005): 49-66.
[9] Qi Meng, Guolin Ke, Taifeng Wang, Wei Chen, Qiwei Ye, Zhi-Ming Ma, Tieyan Liu. “A Communication-Efficient Parallel Algorithm for Decision Tree.” Advances in Neural Information Processing Systems 29 (NIPS 2016).
[10] 如何看待微軟新開源的LightGBM?
[11] 開源|LightGBM:三天內收穫GitHub 1000+ 星

