• 說明
• 問題 識別毒酒
• 方法1 視為一個有約束的最優化問題進行求解
  • 1 模型的進一步討論
• 3方法2 使用編碼的方法
  • 1 結論
  • 2 具體方法
  • 3一個瑕疵和改進的方法
  • 4如果再考慮所需時間最少怎麼辦
  • 5 本方法所能支援的數量上限
• 歡迎提供更多的方法

0.說明

• 本文是雞年新年計劃的內容之一：每週學習一個數學模型，寫一篇總結，記錄自己學到的東西和遇到的問題。
• 這些文章並不是相關模型的全面介紹，也不是從最基礎的開始，所以不一定適合數學模型的beginner，但都是些很實際的技術，希望能幫到你。
• 這個問題可以使用多種方法（或模型）解決，本文給出了使用最優化模型和二維編碼的方法，但彼此之間的效率差距很大，如果你還知道其他解決方法，歡迎你給我留言！我會不定期更新。

1. 問題 ：識別毒酒

請諸位為烏有國王出個主意：有500桶酒，其中1桶是毒酒；毒酒喝下去會在之後的第23-24小時內讀法身亡；48小時後要舉行酒會；國王決定用囚犯來試酒。
不介意囚犯死多少，只要求用最少的囚犯來測試出哪一桶是毒酒，問最少需要多少囚犯才能保證找出毒酒？

2. 方法1： 視為一個有約束的最優化問題進行求解

新增一個假設：毒酒經充分稀釋後仍然致命。
最容易想到的當然是n分法，既高數上的二分法的擴充套件，以下以三分法為例說明：

將500桶編號，每桶取一杯，將500杯平均分成三組，1-166號倒到一個大杯子裡（記為A）、167-333杯（共167杯）倒到一個大杯子裡（記為B）、剩下的167杯倒到一個大杯子（記為C），讓兩個囚犯隨便喝兩杯（比如A和B），23-24小時後根據囚徒的死亡情況就可以判斷毒酒在哪一組。

然後將毒酒所在的組平分為3組，再次安排2個囚犯試喝就可以，……，如此幾次就可以得知哪桶酒是毒酒。

需要說明的是，分三組，但並不需要3個囚徒試喝，只需要2個即可，如上例，若A死掉則毒酒在A組；B死掉則在B組；都沒死則毒酒在C組。

以上是3分法的情況，對於n分法，識別毒酒就是求在滿足(n-1)^m>=500的前提下(n-1)*m的最小值；另外一個約束條件是48小時，所以，最多隻能嘗試兩輪，所以m最多取2

全部模型如下：

需要最多43個囚犯，使用22分法，分兩輪：
500-22*22=16，所以第一輪需要22人；
如果第一輪都活著，毒酒就在剩餘的16裡，第二輪需要16人；
如果第一輪死1個，那麼他喝過的22桶，再用21人去喝，即可確定毒酒在哪一桶。

2.1 模型的進一步討論

如果不考慮m，則所需囚犯數量即為n-1，n越小則所需的人數越少，所需時間越多，n=2時需要9*24小時。那麼，n是否可以為1？

實際上，如果n=1，則上述模型就失效了。但n=1實際上是更簡單的情況，就是讓一個囚犯，先試喝第1桶，24小時之後如果沒事就試喝第2桶，……，以此類推，直至死亡就找到了毒酒。

3方法2： 使用編碼的方法

3.1 結論

先說結論：使用該方法，只需要2個囚犯，具體方法如下（為了方便，假設喝了毒酒之後將在第24個小時時段內毒發身亡）

3.2 具體方法

酒從1-500編號，按照21桶一組平均分開，也就是說，1～21桶是第一組，22～42桶是第2組，…… ，最後一組是第24組，是484-500桶（16桶，注意最後一行有4個0）。如下圖：

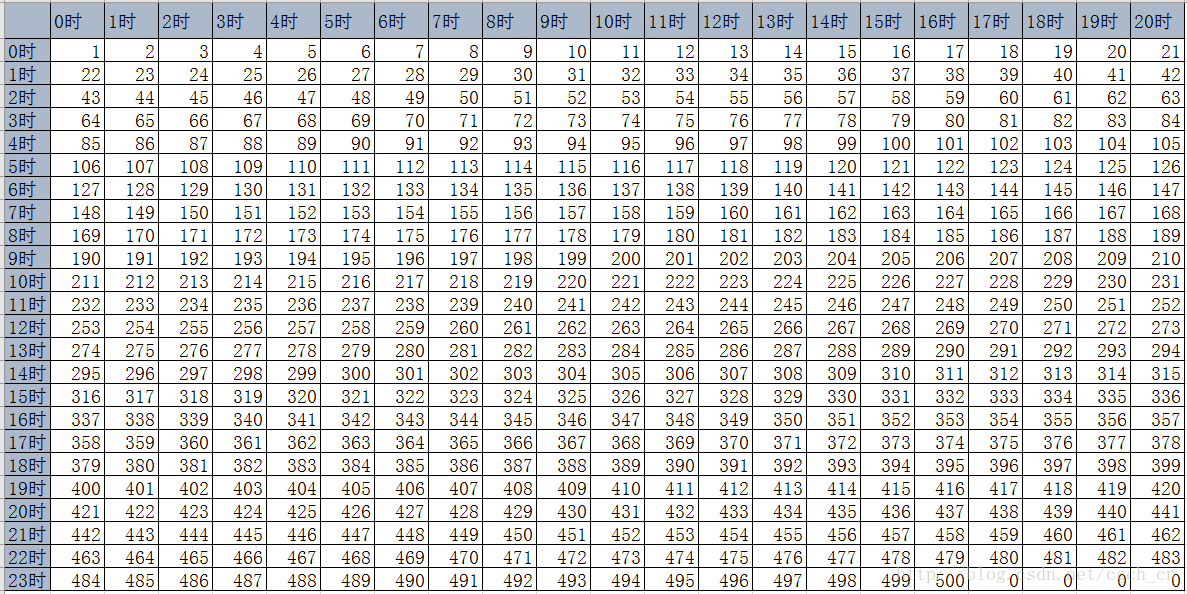
第一個囚犯喝0時刻喝第1組的酒，既第一行的酒，1時刻喝第2組的酒，……23時刻喝484～500的酒（最後一行）；

第二個囚犯0時刻喝每一組的第1桶酒，既第1列的酒，標號1、22、43、……484的酒，1時刻喝每一組的第2桶酒，既第2列的酒，標號2、23、44、……485的酒，……，20時刻喝每一組的第21瓶酒，既第21列的酒，既標號21、42、……、483的酒。

最晚在宴會開始前，兩人都會死亡，根據兩人死的時間就可以推出是哪一桶酒有毒。比如，第一個人死於次日10至11時之間，則其是第一天的11時服的毒酒，屬於上圖的232至252號，第二個人死於次日8至9時，則其是第一天9時服的毒酒，是上圖中的第10列，二者的交叉點是241號，說明第241桶為毒酒。

根據死亡時間確定喝酒時刻的方法是：如果該人死於次日的第 i-1至 i 時，則其喝下毒酒的時刻是第一天的 i 時。
如果死於第一天的23至24時，則為0時喝的酒；死於24至次日1時的是頭天1時喝的酒。

上述方法的實質是對1到500這500個數字進行編碼，本文采取的是用兩個下標進行編碼：行和列，另外，從數制的角度來看，本文的方法使用的是24進位制；這似乎是由毒發間隔來確定的。

3.3一個瑕疵和改進的方法

上述方法有一個瑕疵：題目告知的毒發時段是23至24時，如果理解為兩個小時，則上述方法存在時段重疊問題，會導致無法判斷喝酒時間。

解決方法是間隔兩個小時喝一次酒，那麼，要在兩天內完成測試，必須在24時內完成試喝，每個人試喝的組數不能超過12組，所以分組方法如下圖

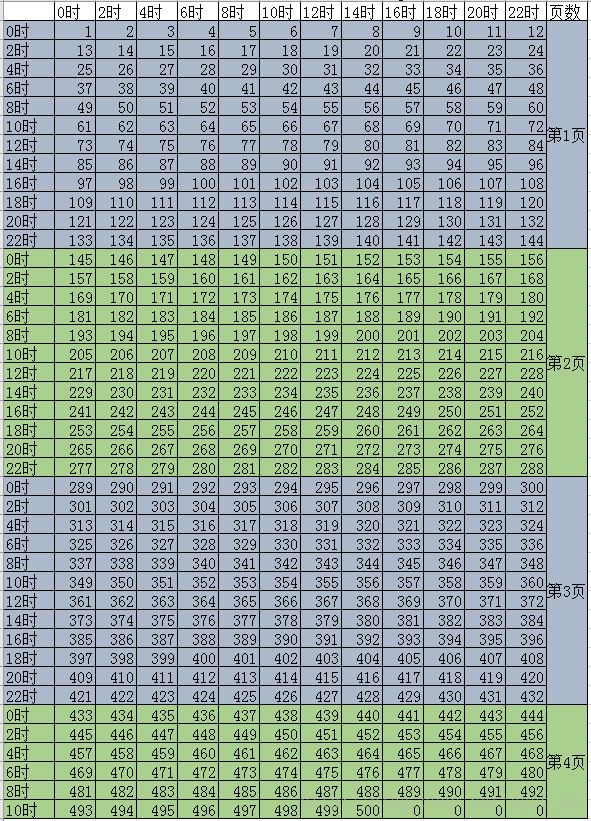
此時帶來的問題是：由於有42行，所以，之前的由一個囚犯按照行進行試喝的方法無法進行。那麼，我們需要4個囚犯按照行進行試喝嗎？

不需要，實際上，我們只需要增加一個囚犯即可，既，讓一個囚犯按照“頁”試喝，具體如下：

第一個：0時刻喝每一頁的第1組的酒，既每一頁第1行的酒，既1至12號、145至156號、289至300號、433至444號；2時刻喝每一頁的第2組的酒，既每一頁第2行的酒，……22時刻喝每一頁的第12組的酒，既每一頁第12行的酒，

第二個囚犯0時刻喝每一頁的第1列，既上圖的第1列的所有酒，標號1、13、25、……、493的酒，2時刻喝每一頁的第2列，既第2列的酒，……，22時刻喝每一頁的第12列的所有酒，既第21列的酒，既標號12、24、……、492的酒。

第三個囚犯0時刻喝第一頁的所有酒，既1至144號，2時刻喝第二頁的所有酒，既145至288號，4時刻喝第三頁的所有酒，289至432號，6時刻喝剩餘的。

同樣根據三個人的死亡時間可以確定毒酒的編號。
大家也可以結合下圖理解上述方法：

3.4如果再考慮所需時間最少怎麼辦？

如果不僅要所需囚犯最少，也要所需時間最少，則上述500桶可以分成8行8列8頁，如下圖：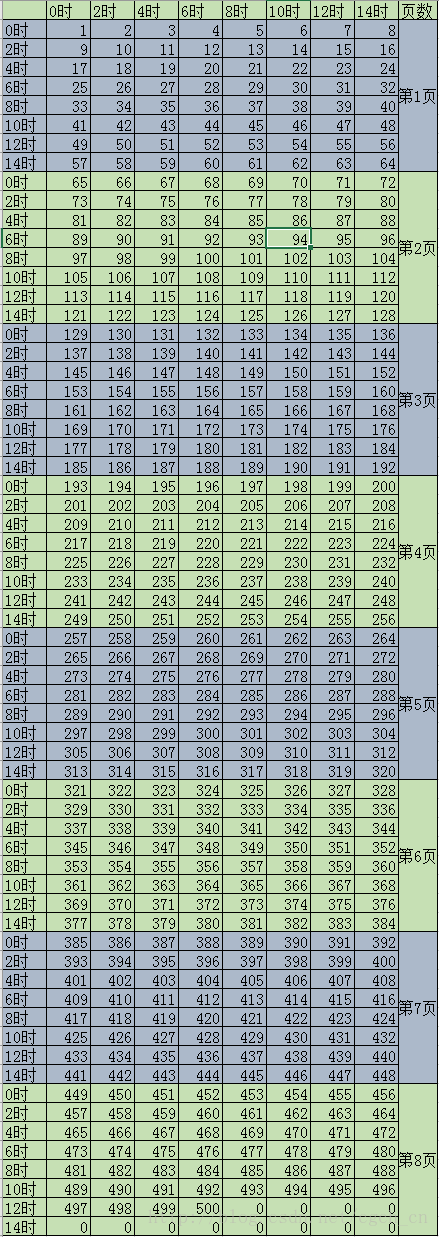
採取相同的方法，最晚可以在次日14:00時找到毒酒。

3.5 本方法所能支援的數量上限

如果毒發時間是在服毒後的第24個小時內，而不是23至24時，則兩個囚犯所能檢測的最大數量為24*24=576桶，超過這個數字則兩個囚犯就不夠了；

同樣的假設下，三個囚犯所能檢測的最大數量為24^3=13824桶；

n個囚犯所能檢測的最大數量為24^n

4. 歡迎提供更多的方法

顯然，第二種方法更好，也更驚豔，歡迎大家提供更多的思路和方法。