目錄

• Two-Finger演算法
  • 前提
  • 概要
  • 步驟一：移動物件
  • 步驟二：更新指標
  • 優缺點
• 表格演算法
  • 概要
  • 步驟一：移動物件群 和 構築間隙表格
    • 移動物件群
    • 構築間隙表格
  • 步驟二：更新指標
  • 優缺點

Two-Finger演算法

Robert A.Saunders 對堆執行兩次搜尋

前提

Two-Finger 演算法，必須將所有物件整理成大小一致。它沒有在物件的頭中設立forwarding指標，而是在物件的域中設立forwarding指標

概要

Two-Finger演算法由一下兩個步驟構造。

• 移動物件
• 更新指標

在Lisp2演算法中，是將物件移動到堆的一端。在Two-Finger中，操作物件向左滑動，通過執行壓縮演算法來填補空閒空間。此時為了讓更好的填補空間，所以物件大小必須一樣。

移動前的物件都會被保留（圖的白色物件）。因為在Two-Finger演算法中，我們要利用放置非活動物件的空間來作為活動物件的目標空間，這是為了讓移動前的物件不會在GC過程中被覆蓋掉。這樣一來，我們就能把forwarding指標設定在這個移動前 的物件的域中，沒有必要多準備出 1 個字了。

步驟一：移動物件

• $free和live兩個指標，從兩端向正中間搜尋堆。
• $free是用於尋找非活動的指標，live是尋找活動物件(原空間)

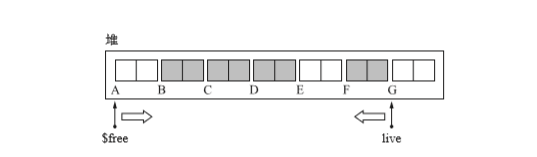
• 兩個指標發現空間和原空間的物件時會移動物件。

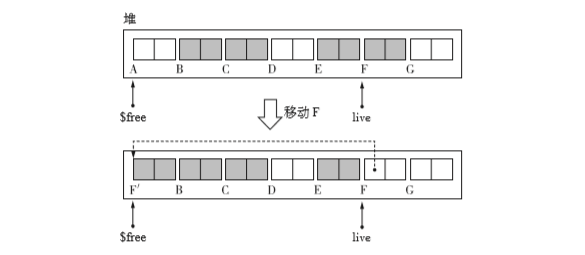
• 途中虛線其實表示forwarding。
• 之後使用move_obj函式對物件進行移動其虛擬碼如下：

move_obj(){
    $free = $heap_start
    live = $heap_end - OBJ_SIZE
    while(TRUE)
        while($free.mark == TRUE) //從前往後尋找非活動物件
            $free += OBJ_SIZE
        while(live.mark == FLASE) // 重後往前 尋找活動物件
            live -= OBJ_SIZE
        if($free < live)   // 判斷交換條件
            copy_data($free, live, OBJ_SIZE)
            live.forwarding = $free
            live.mark = FALSE
        else
            break
}
 

• 先從前往後，使用$free尋找非活動物件。
• 在從後往前，使用live尋找活動物件。
• 找到之後，判斷兩者位置。如果非活動物件在活動物件之前，就執行復制操作。否則就退出迴圈。

步驟二：更新指標

接下來尋找指向移動前的物件的指標，把它更新，使其指向移動後的物件。更新指標操作的是adjust_ptr()函式。

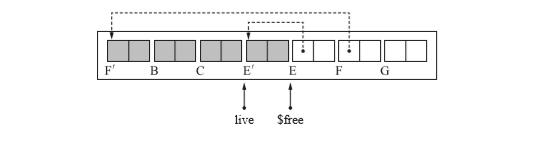
• 當物件移動結束時，$free 指標指向分塊的開頭，這時位於 $free 指標右邊的不是非活動物件就是活動物件。
• $free右邊地址的指標引用的是移動前的物件。

adjust_ptr(){
    for(r :$roots)
        if(*r >= $free)
            *r = (*r).forwarding
    
    scan = $heap_start
    while(scan < $free)
        scan.mark = FALSE
        for(child :children(scan))
            if(*child >= $free)
                *child = (*child).forwarding
            scab += OBJ_SIZE
            
}

• 先查詢根直接引用的物件。當這些指標的物件在$free右邊的時候,就意味這個物件已經被移動到了某處。在這種情況下必須將指標的引用目標更新到移動後的物件。
• 所有活動物件都在$heap_start 和 $free之間，我們需要取遍歷這一部分堆。

優缺點

優點：Two-Finger 演算法能把 forwarding 指標設定在移動前的物件的域裡，所以不需要額外的記憶體 空間以用於 forwarding 指標。只需要2次搜尋堆。

缺點： Two-Finger 演算法則不考慮物件間的引用關係，一律對其進行壓縮，結果就導致物件的順序在壓縮前後產生了巨大的變化。因此，我們無法更好的使快取。 物件大小必須一樣。

表格演算法

B.K.Haddon 和 W.M.Waite， 1967

這個演算法使用表格來進行壓縮，和Two-Finger一樣都是執行兩次壓縮。

概要

表格演算法通過以下2個步驟來執行壓縮。

1. 移動物件以及構築間隙表格(break table)
2. 更新指標

步驟1是讓連續的活動物件群一併移動。（和前面所接觸到的壓縮演算法都不同）。除此之外還要預留更新指標所用到的資訊，這裡我們使用間隙表格。

間隙表格，大概意思是“按照一個個活動物件群記錄下壓縮所需要的資訊的表格”。這個表格事先放入移動前的物件群資訊（位於物件群的首地址和較低地址的分塊的總大小）。為了方便地址計算，我們將1個字的大小定為50.如下圖示：

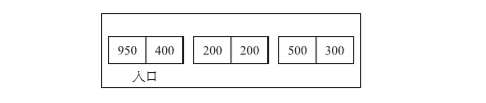
• 各個入口左邊的值是活動物件群的首地址，右邊的值是分塊的總大小。隨著物件的移動，它會被放置在空閒空間裡。不過，間隙表格的各個入口需要2個位元組。也就是說，這演算法的其中一個限制條件就是，每個物件都必須在2個位元組以上。
• 步驟2，更新每個指標。

步驟一：移動物件群 和 構築間隙表格

移動物件群

活動物件群移動前和移動後(move_obj())的狀態如圖示：

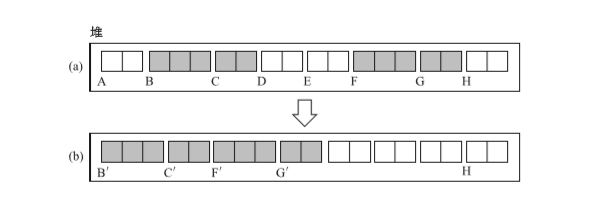
move_obj(){
    scan = $free = $heap_start
    size = 0
    while(scan < $heap_end)  // while 迴圈 1
        while(scan.mark == FALSE) 
            size += scan.size
            scan += scan.size
        live = scan
        while(scan.mark == TRUE) // while 迴圈 2
            scan += scan.size
        slide_objs_and_mark_bt(scan ,$free, live, size)
        $free += (scan-live)
}

• scan用於尋找活動群物件，從堆頭開始搜尋。
• $free是指向物件群目標空間的指標，size是保持分塊大小的變數。這裡的分塊是指用來記錄到間隙表格裡的分塊。
• 第一個while中，scan指標負責尋找活動物件的群的開頭。也就是說，直到它尋找到活動物件為止，都會跳過非活動物件。於此同時使用size計算scan指標跳過的空間大小。
• scan是指標，size是整數。
• 搜尋結束時候，scan指標指向活動物件群開頭。這個為止記錄在live指標裡。
• 之後繼續使用scan，搜尋連續的多動物件群。（一次找對活動物件迴圈完畢）

這時，堆的狀態如下圖示：

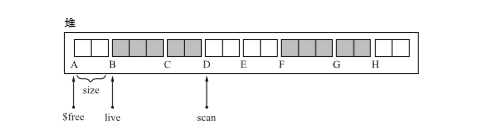
在第二個while迴圈中

• 其中slide_objs_and_make_bt()函式中執行活動物件群和構築間隙表格的操作。物件群的原空間是live，目標空間是$free，要移動的物件群的總大小是scan-live。
• 最後一行，準備下一次移動，將$free移動scan-live個大小，即$free向後移動大小等於物件群的大小。如下圖示：

• 這裡和Lisp2演算法一樣，都是通過把活動物件左滑壓縮。不過這裡是移動連續的物件群。

構築間隙表格

在上一個圖中，每次移動物件群的時候都需要吧資訊註冊到間隙表格中。註冊入口是物件群的首地址live和物件群滑動大小size的組合。如下圖示：

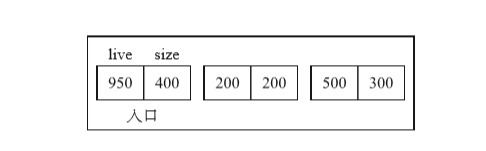
構築間隙表格是在slide_objs_and_mark_bt()方法中指向的，下面使用圖例來說明過程：

• 間隙表格構築有以下兩項操作構成。
  • 移動物件群
  • 移動間隙表格
• 下圖示()內數字表格各個物件的首地址，設1個字的大小為50

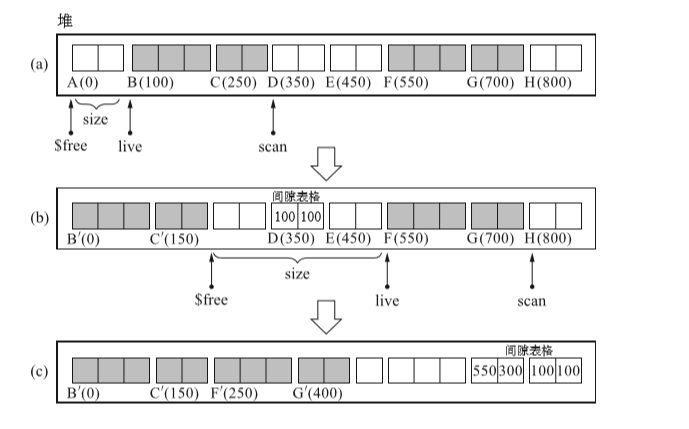
• 如中a部分，在移動物件群BC的同時構築間隙表格。將BC的首地址100以及BC最左邊的分塊大小100組合成一對，通過scan指標寫入已知分塊的350號地址。
• b部分，在這裡進行的是移動物件群FG的操作。這時候要註冊到間隙表的的資訊是(550, 300)不過不能直接將該資訊寫入(100, 100)之後（450塊）因為物件群要移進去。
• 這時候，我們有的間隙表格移動到FG後面也就是700號地址裡。
• 完成後狀態如e所示。注意間隙表格的入口順序，各個入口不是按入口裡的第一元素排列的，也就是說，不是按活動物件群的首地址live進行排列的。
  • 在b中，因為間隙表格妨礙到物件FG的移動，所以先讓它迴避到800,之後在移動FC將新的表格註冊到了700上。
  • 像這樣往已有的間隙表格中新追加入口時，會有表格左側空閒的情況，在這種情況下，入口順序只能亂了。
  • 當然也可以按照順序排列，如論是在新增的時候按順序，或者新增完之後排序，它都要花費一定的空間和時間。
• 因為沒有按照第一元素live的順序排列，所以增大了更新指標的計算量。

步驟二：更新指標

在dajust_ptr()函式中，將引用移動前的物件的指標全部換成引用移動後的物件的指標。這項操作本身和前面的兩個演算法中的操作是相同的。

adjust_ptr(){
    for(r :$roots)
        *r = new_address(*r)
        
    scan = $heap_start
    while(scan < $free)
        scan.mark = FALSE
        for(child : children(scan))
            *child = new_address(*child)
        scan += scan.size
        
}

下面是new_address(obj)函式

new_address(obj){
    best_entry = new_bt_entry(0, 0)
    for(entry :break_table)
        if(entry.address <= obj && $best_entry.address < entry.address)
            best_entry = entry
    return obj - best_entry.size
    
}

• 這個函式返回引數obj移動後的地址，在其中new_bt_entry(0, 0)函式中生成虛擬間隙表格的入口。
• for迴圈負責調查間隙表格，在持有obj及其一下地址的入口中尋找最大的入口。這樣一來就得到了持有obj所屬物件群資訊的入口。這個入口就是best_entry
• 如果間隙表格裡的入口是按照地址順序整齊排列的，我們就有可能用二分查詢有效地址查詢到best_entry。但是間隙表格的入口並不是整齊排列的，因此就需要通過上面這種方式來查詢。
• best_entry是一個入口，這個入口持有obj所屬物件群移動前的資訊。屬於這個物件群的物件都會被向左移動best_entry.size個大小。因此obj移動後的地址變成了obj-best_entry.size。

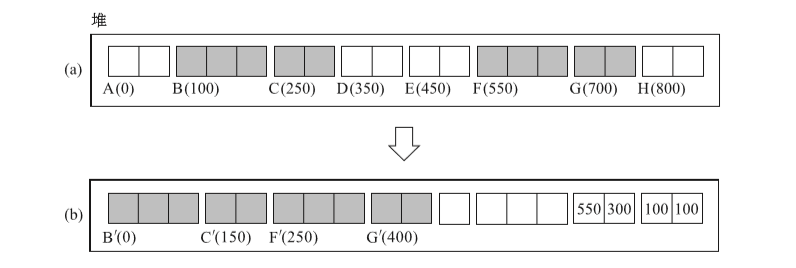
上圖中如果我們想知道B移動到了BꞋ，首先就要以B的地址100為線索調查間隙表格，然後就會發現入口（100，100）是best_entry，接下來可由B的地址 100 求得 best_entry.size，即將 B 的地址減去 100 得到 BꞋ 的地址 0。 同理，我們可以從 F 的地址 550 減去入口（550，300）中的 300，得到 FꞋ 的地址 250。

優缺點

優點：演算法很好地利用了分塊，保留了更換指標所必要的資訊。（沒有為壓縮備出多餘空間，）並且它沒有改變物件的順序，所以可以通過快取來提高物件的訪問速度。

缺點：維持間隙表格需要付出很高的代價，每次移動物件群都要對錶格進行操作。