一、引言

　　多項式函式常常用於描述現實世界的各種規律，而在用計算機計算多項式的值的時候，不同演算法的計算時空複雜度通常不一樣。如一個n次多項式

　　f(x)=a[n]x^n+a[n-1]x^(n-1)+......+a[1]x+a[0],我們的常規計算辦法是，直接計算，這樣我們的時間複雜度為:O(n^2)

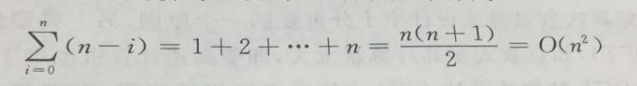
下面我們介紹秦九韶演算法：

其核心思想：後面每一次計算都依賴於前面計算的結果，這樣以減少重複的計算。

簡單引例:

       計算 x^8 直接算將算8次乘法，而這8次都是必要的嗎？顯然不是，當我們知道x^2的值後，計算x^4只需要用x^2*x^2即可。秦九韶演算法正是這樣來減少計算量的。

一、推導

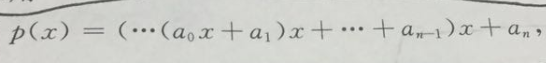
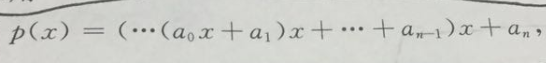
　　a0--->an依次是最高項，到常數項係數

　　從而bn就是所求的解。

以上引用自：https://www.cnblogs.com/jake9402/p/7570129.html#4121459

3、演算法實現

情況一：假設cone[] 陣列中存的多項式的係數cone[0]是0階的係數以此類推cone[n]就是n階係數

//n是係數的最高階數
    public int calculation(int x,int[] cone,int n){
        int b=a[n];
        
 
for(int i=0;i<n;i++){
            b=b*x+a[n-i-1];    
        }
        return b;
    }

情況二：假設cone[]陣列中存的多項式的係數cone[0]是n階的係數以此類推cone[n]就是0階係數,則程式碼如下

    public int calculation(int x,int[] cone,int n){
        int b=a[0];
        for(int i=0;i<n;i++){
            b=b*x+a[i+1];    
        }
        
 
return b;
    }

邏輯一定要理順