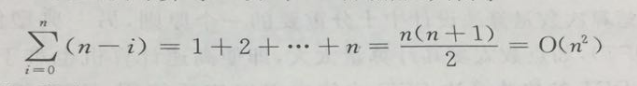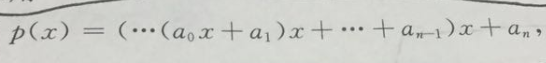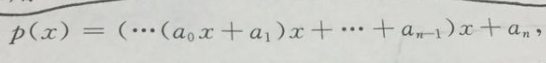秦九韶演算法的思想與解多項式演算法時間比較附程式碼
多項式計算之秦九韶演算法
多項式求值與秦九韶演算法
一、引言
多項式函式常常用於描述現實世界的各種規律,而在用計算機計算多項式的值的時候,不同演算法的計算時空複雜度通常不一樣。如一個n次多項式
f(x)=a[n]x^n+a[n-1]x^(n-1)+......+a[1]x+a[0],我們的常規計算辦法是,直接計算,這樣我們的時間複雜度為:O(n^2)
下面我們介紹秦九韶演算法:
其核心思想:後面每一次計算都依賴於前面計算的結果,這樣以減少重複的計算。
簡單引例:
計算 x^8 直接算將算8次乘法,而這8次都是必要的嗎?顯然不是,當我們知道x^2的值後,計算x^4只需要用x^2*x^2即可。秦九韶演算法正是這樣來減少計算量的。
一、推導
a0--->an依次是最高項,到常數項係數
從而bn
三、演算法描述
由以上推導知,bn就是我們所求的值,要求bn就得逆推到b0,由於b0=a0我們就可以求出b1依次下去就可以求出bn。
資料結構:
1.陣列
1.a[]用於儲存係數
ps:一般做法還需要儲存b[],我們這裡只是用到前一項,所以一個常數即可
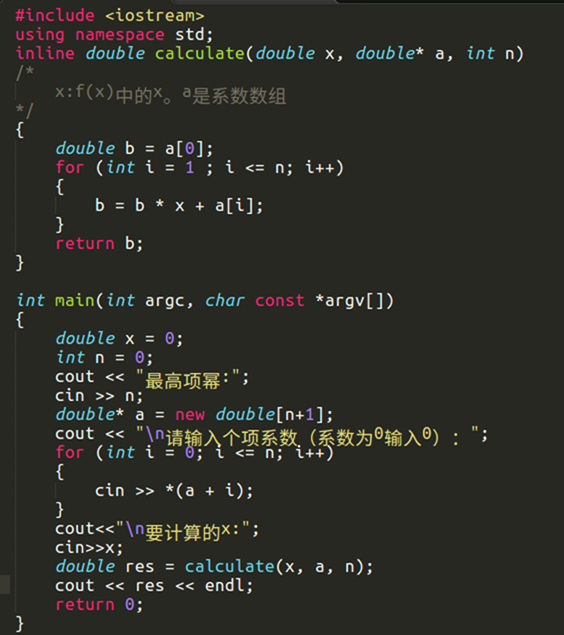
c++實現:

#include <iostream> using namespace std; inline double calculate(double x, double* a, int n) /* x:f(x)中的x。a是係數陣列 */ { double b = a[0]; for (int i = 1 ; i <= n; i++) { b = b * x + a[i]; } return b; }
int main(int argc, char const argv[])
{
double x = 0;
int n = 0;
cout << “最高項冪:”;
cin >> n;
double a = new double[n+1];
cout << “\n請輸入個項係數(係數為0輸入0):”;
for (int i = 0; i <= n; i++)
{
cin >> *(a + i);
}
cout<<"\n要計算的x:";
cin>>x;
double res = calculate(x, a, n);
cout << res << endl;
return 0;
}

MyTest.cpp : 定義控制檯應用程式的入口點。
/*
時間測量函呼叫
*/
#include "stdafx.h"
#include <stdio.h>
#include <time.h>
#include <math.h>
#pragma warning(disable:4996)
#define MAXN 10
#define MAXK 1e4
//代表10的7次方
/*f(x)=a0 +a1*x+a2*x*x+a3*x*x*x +...+an*x的N次方 */
clock_t start,stop;
/*clock_t是clock()函式返回的變數的型別*/
double duration;
/*記錄被測函式執行的時間,以秒為單位*/
double f1(int n, double a[], double x){
int i;
double p = a[0];
for (i = 1; i <= n; i++){
p += a[i] * pow(x, i);
}
return p;
}
/* 秦九韶演算法 */
double f2(int n, double a[], double x){
int i;
double p = a[n];
for (i = n; i > 0; i--){
p = a[i - 1] + x*p;
}
return p;
}
int _tmain(int argc, _TCHAR* argv[])
{
/*不在測試範圍內的準備函式,寫在開始之前*/
int i;
double a[MAXN];
for (i = 0; i < MAXN; i++)a[i] = (double)i;
start = clock();
for (i = 0; i < MAXK;i++)
f1(MAXN - 1, a, 1.1);
stop = clock();
duration = ((double)(stop - start)) / CLK_TCK / MAXK;
/*其他不在測試範圍外的處理寫在後面*/
printf("ticks1 = %f\n", (double)(stop - start));
printf("duration1 = %6.2e\n", duration);
start = clock();
for (i = 0; i < MAXK;i++)
f2(MAXN - 1, a, 1.1);
stop = clock();
duration = ((double)(stop - start)) / CLK_TCK/MAXK;
/*其他不在測試範圍外的處理寫在後面*/
printf("ticks2 = %f\n", (double)(stop - start));
printf("duration2 = %6.2e\n", duration);
/*%6.2e 表示6表示輸出長度(包含小數點),2表示輸出小數點位數,
d表示輸出為十進位制
e表示用科學計數法表示*/
return 0;
}