Machine Learning筆記整理 ------ (三)基本效能度量
1. 均方誤差,錯誤率,精度
給定樣例集 (Example set):
D = {(x1, y1), (x2, y2), (x3, y3), ......, (xm, ym)}
其中xi是對應屬性的值,yi是xi的真實標記,評估模型效能,即將預測結果f(x)與真實標記y進行比較。
對於迴歸任務:均方誤差 (Mean squared error)
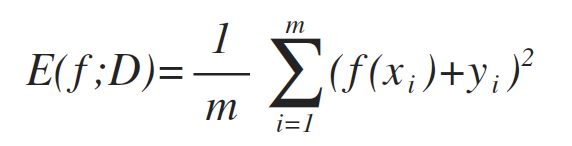
更一般的,對於資料分佈D和概率密度函式p(·),均方誤差可描述為:
![]()
錯誤率 (Error rate):分類錯誤樣本數佔總樣本數比例(其中,II(·)為指示函式,在·為真假時分別取1和0):

相應的精度 (accuracy) 可以定義為:
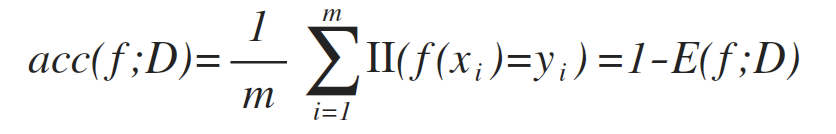
更一般的,對於資料分佈D和概率密度函式p(·),錯誤率和精度可描述為:
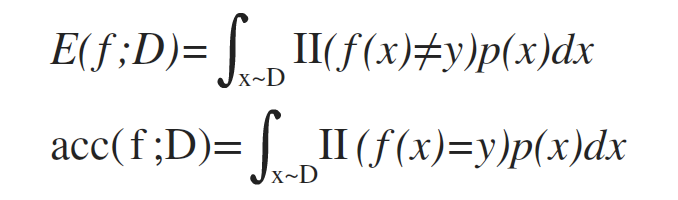
2. 混淆矩陣,查準率,查全率,Fβ度量
(1) 混淆矩陣 (Confusion matrix)
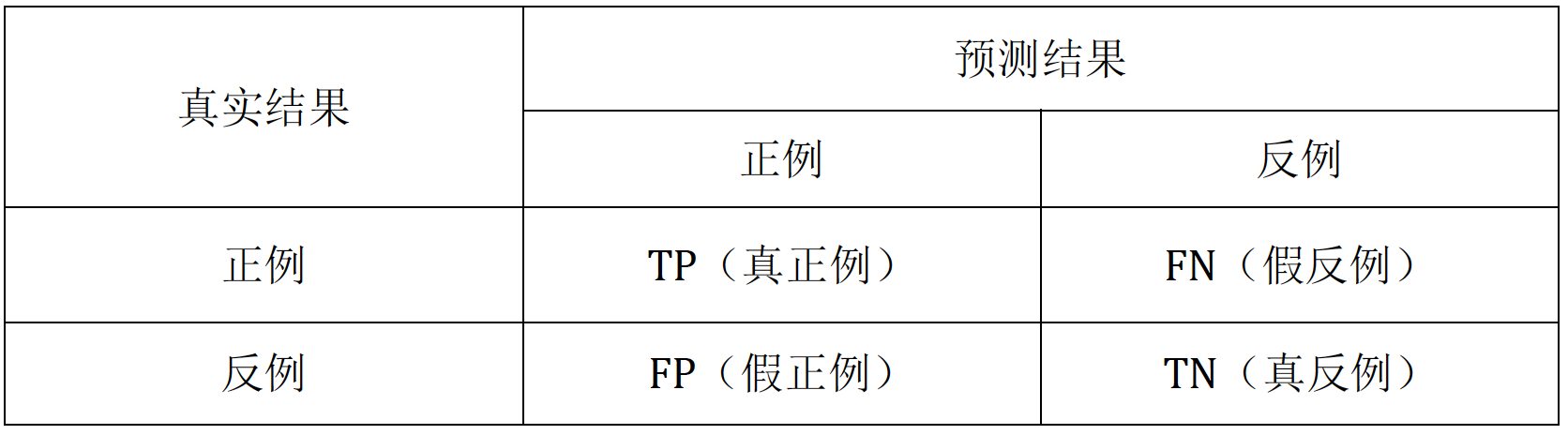
真正例TP(True positive):將正例預測為正例(正確)
假反例FN(False negative):將正例預測為反例(錯誤)
假正例FP(False positive):將反例預測為正例(錯誤)
真反例TN(True negative):將反例預測為反例(正確)
即:T和F表示預測的結果是否正確,P和N表示模型預測的結果為正或反,故只要是F那麼前後一定不一致。
1 #!/usr/bin/env python32 3 from sklearn import metrics 4 5 # titanic.y為實際標籤集合,titanic_y_pred為模型預測的標籤集合 6 confusion_matrix = metrics.confusion_matrix(titanic.y, titanic_y_pred) 7 8 TP = confusion_matrix[1, 1] 9 TN = confusion_matrix[0, 0] 10 FP = confusion_matrix[0, 1] 11 FT = confusion_matrix[1, 0]
輸出結果: (245, 455, 94, 97)
(2) 查準率 (Precision),查全率 (Recall)
查準率和查全率的定義如下:

一般而言,查準率P和查全率R是一對相互矛盾的效能度量指標,例如,如果想將某類別A全部選出來,只需要增加選取的數量,若樣本總數為m,將m個樣本全部選出來,即所有樣本都被選中,自然包括了全部類別為A的樣本,查全率R自然會很高,而查準率很差;相對應的,如果僅僅選取最有把握的樣本,則會漏掉不少正確的樣本,查準率會很高,查全率則會很低。
(3) P-R曲線 (P-R Curve),平衡點(Break-Even Point, BEP)
以查全率R為橫軸、查準率P為縱軸,可以做P-R曲線與P-R圖,即:
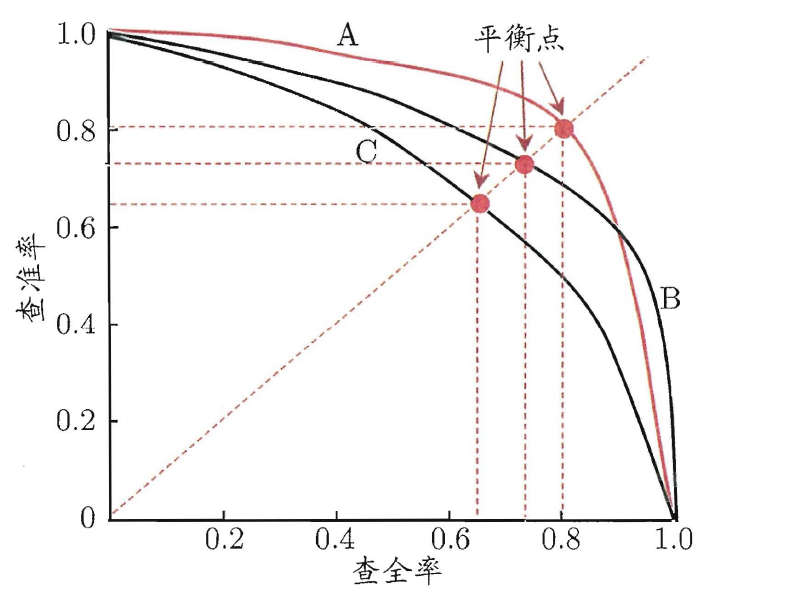
Area(A) > Area(C),則模型A的效能優於C
Area(B) > Area(C),則模型B的效能優於C
但如上圖所示,A、B相交難以直接判斷,故可以使用平衡點來進行判斷,平衡點(Break-Even Point,BEP)的定義是:當 查準率P = 查全率R時,兩者的取值,可作f(x)=x,找與AB曲線相交的交點即為平衡點,所以,上圖中,模型A的效能優於模型B的效能。
(4) F1度量,Fβ度量,巨集度量,微度量
F1度量是基於查準率和查全率的調和平均(harmonic mean)定義的,即:

故有F1度量的表示形式:

而F1度量的一般形式Fβ度量,則是基於查準率和查全率的加權調和平均定義的:

故有Fβ度量的表示形式:

總結:
- 當β = 1時,為F1度量
- 當β > 1時,查全率影響較大
- 當β < 1時,查準率影響較大
- 即當β > 0時,度量了查全率對查準率的相對重要性
綜上所述,對於二分類任務,可以做多個混淆矩陣(多次訓練、測試)/(多個訓練集訓練、測試),若為多分類任務,則可以以每兩兩類別的組合對應一個混淆矩陣,在n個二分類混淆矩陣上綜合考察查準率P和查全率R。更直接的做法是使用巨集查準率(marco-P)與巨集查全率(marco-R)以及相應的巨集F1度量(marco-F1):

同樣,將個矩陣元素平均,可以得到TP、FP、TN和FN的平均值,再計算得出微查準率(micro-P)與微查全率(micro-R)以及對應的微F1度量(micro-F1):

3. ROC (Receiver Operating Characteristic),AUC(Area Under ROC Curve)
(1) ROC(Receiver Operating Characteristic) 受試工作者特徵
ROC曲線的橫軸為假正例率FPR(False Positive Rate),縱軸為真正例率(True Positive Rate),兩者的定義如下:
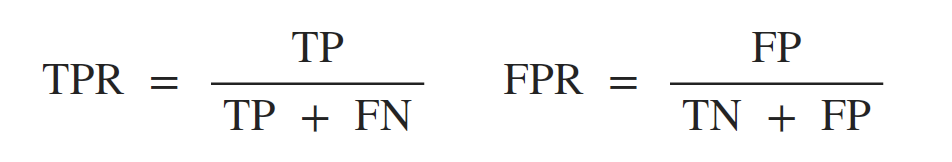
根據預測結果,對樣例進行排序,按此順序逐個把樣本作為正例進行預測,每次計算出FP和TP並作圖,即得到ROC曲線,下圖中(a)對角虛線對應於“隨機猜測”模型。另,ROC曲線僅適用於二分類模型(前提在於選定閾值)。
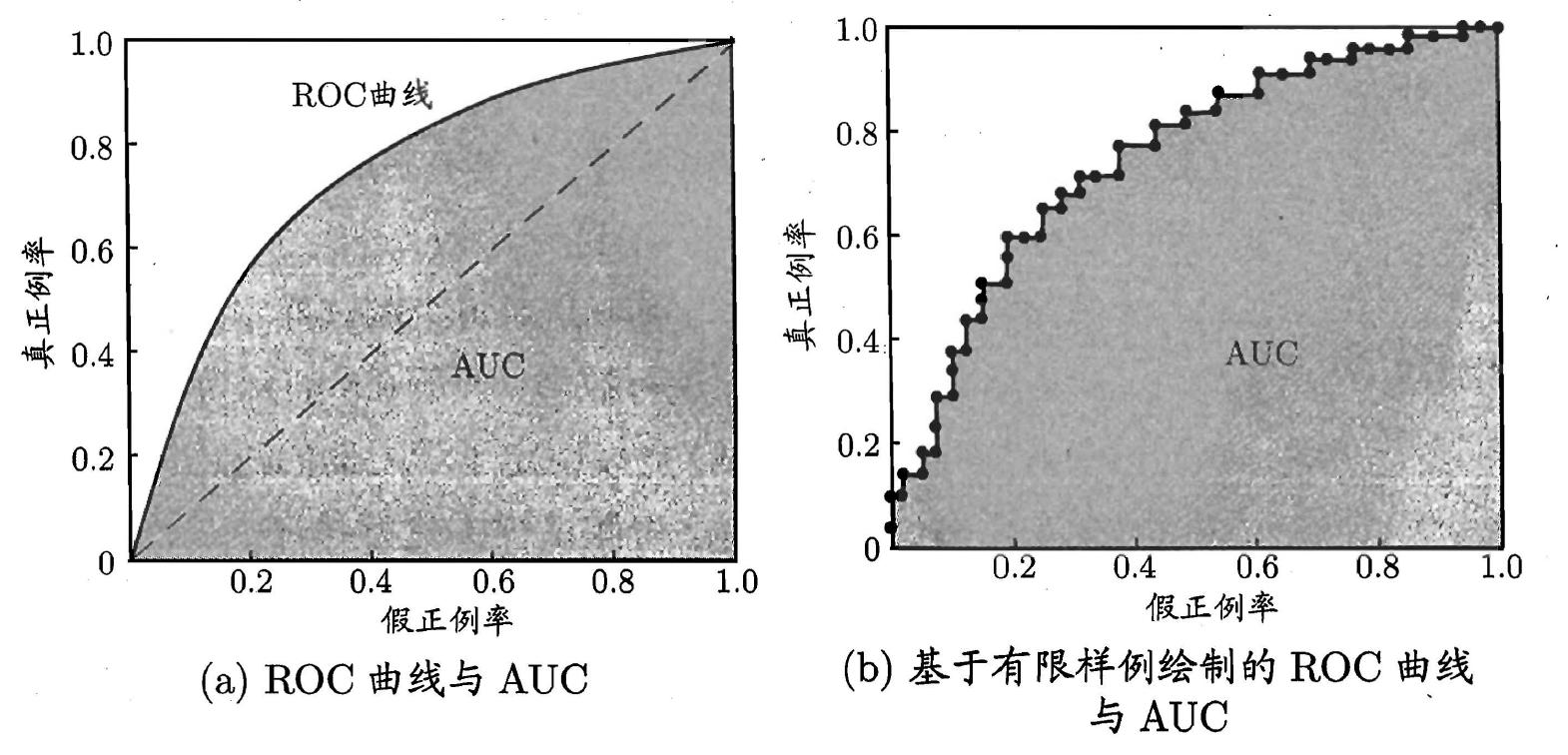
(2) AUC(Area Under ROC Curve)ROC曲線下面積
AUC即ROC曲線下對應面積,可以使用如下方式計算:
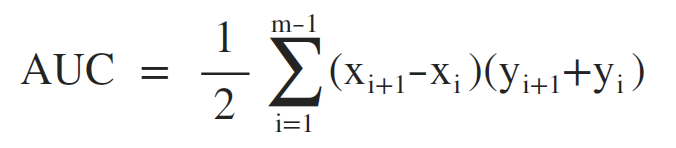
意義:從所有類別為1的樣本中隨機選取一個樣本,再從所有類別為0的樣本中隨機選取一個樣本,用模型進行預測,將1預測為1的概率為p1,將0預測為0的概率為p0,p1>p0的概率即為AUC的值。所以,AUC的值不會超過1,而且越接近1則表示模型的效能越好。
附:平均數、方差、標準差及置信區間的計算公式(之前寫畢業論文時,導師要求對每個建模的結果求出對應95%情況下的置信區間)
平均數 (Mean)
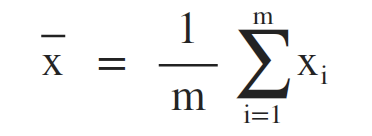
方差 (Variance)
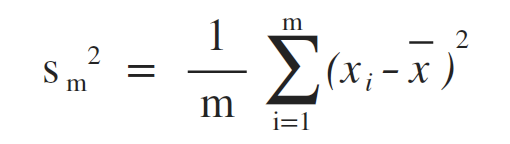
標準差 (Standard Variance)
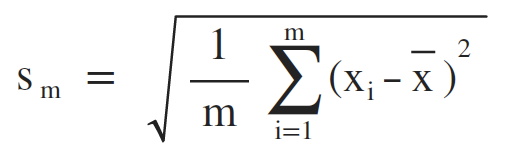
置信區間 (Confidence Interval)
置信區間的意義在於表徵資料結果的可信程度,其區間的上下限為:
![]()
當90%,n = 1.645;當95%時,n=1.96;當99%時,n=2.576(其餘對應值可查表)。
