資料結構實現 6.1:二叉堆_基於動態陣列實現(C++版)
資料結構實現 6.1:二叉堆_基於動態陣列實現(C++版)
1. 概念及基本框架
二叉堆 是一種高階資料結構,這裡我們通過 1.1 中的 動態陣列 來實現。
因為二分搜尋樹操作的時間複雜度(O(logn)
為此,我們需要理解幾個與二叉樹有關的概念。
1.1 滿二叉樹
滿二叉樹作為二叉樹的一種,有著如下特性:
1.最後一層的結點(葉子結點)的左右子結點均為空。
2.除葉子結點外,其他結點的左右兩個子結點均不為空。
3.若滿二叉樹有 k 層,那麼整棵滿二叉樹一共有 2^k - 1 個結點。
4.若記根節點為第 0 層,滿二叉樹的第 n 層結點一共有 2^n 個結點。
5.滿二叉樹的前 n
注:滿二叉樹對結點儲存的資料大小並沒有特殊要求。
下圖給出的就是一棵滿二叉樹:
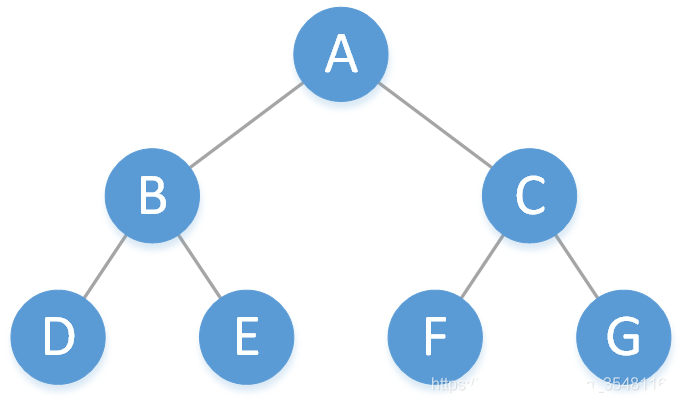
1.2 完全二叉樹
完全二叉樹也是二叉樹的一種,它是由滿二叉樹引出來的,完全二叉樹有如下特性:
1.若完全二叉樹有 k 層,那麼樹的前 k - 1 層是一棵滿二叉樹。
2.若該樹不是滿二叉樹,那麼第 k 層的結點全部連續集中在左邊。
3.若完全二叉樹有 k 層,那麼整棵完全二叉樹一共有 2^(k - 1) ~ 2^k - 1 個結點。
注:滿二叉樹是完全二叉樹的一種特例。
下圖給出的就是一棵完全二叉樹:
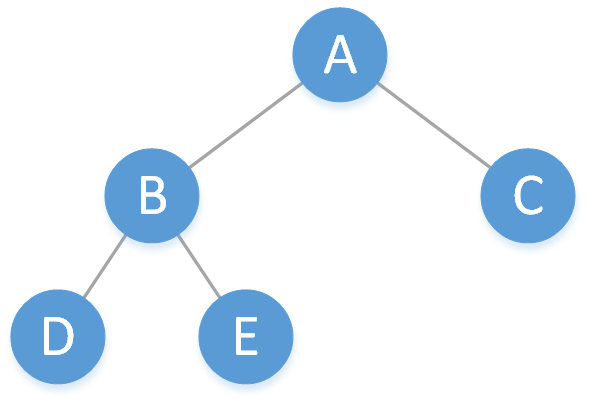
接下來,我們嘗試用陣列的儲存結構,完全二叉樹的邏輯結構來建立一個二叉堆。
首先,我們先定義一個二叉堆的類,我們不給出建構函式,編譯器會預設實現。
template <class T>
class MaxHeap{
...
private:
Array<T> arr;
};
這裡為了避免重複設計就可以相容更多資料型別,引入了 泛型 ,即 模板 的概念。(模板的關鍵字是 class 或 typename)
對於陣列而言,為了降低操作的時間複雜度,我們最好選擇在陣列的末尾增、刪元素;而對於完全二叉樹的新增元素操作可以看作是由根結點從左至右一層一層的新增元素,儲存上與邏輯上的關係如下:

所以能夠得到結點之間索引的關係就顯得至關重要。
其實不難發現,若記一個結點的索引為 i ,那麼其左邊的子結點索引是 2 * i + 1 ,而其有右邊的子結點索引是 2 * (i + 1) 。所以,我們可以在類中實現這樣的幾個函式,來獲得邏輯結構上某一結點對應陣列位置的索引。
template <class T>
class MaxHeap{
...
private:
int parent(int index){
if (index <= 0 || index >= arr.size()){
return NULL;
}
return (index - 1) / 2;
}
int leftChild(int index){
return index * 2 + 1;
}
int rightChild(int index){
return (index + 1) * 2;
}
...
};
parent :返回父結點的索引
leftChild :返回左邊子結點的索引
rightChild :返回右邊子結點的索引
二叉堆有兩種,最大堆和最小堆,這裡我們要實現的就是一個最大二叉堆。
將最大二叉堆看成二叉樹結構會有如下性質:
1.最大二叉堆是一棵完全二叉樹。
2.每個結點的值 大於等於 其左右子結點的值,即最大二叉堆存放的資料要具有可比性。
注:最小二叉堆性質可以類比。
下圖就是一個最大二叉堆:
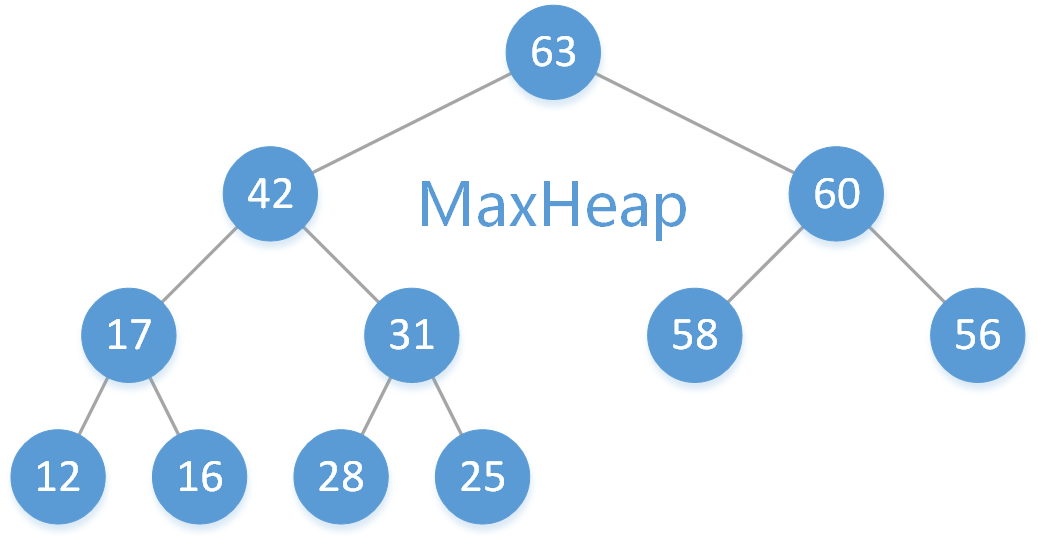
接下來我們就對最大二叉堆的增、刪、查以及一些其他基本操作用程式碼去實現。
2. 基本操作程式實現
2.1 增加操作
對於最大二叉堆的增加操作而言我們可以先從邏輯結構上進行推理,然後利用陣列去實現。
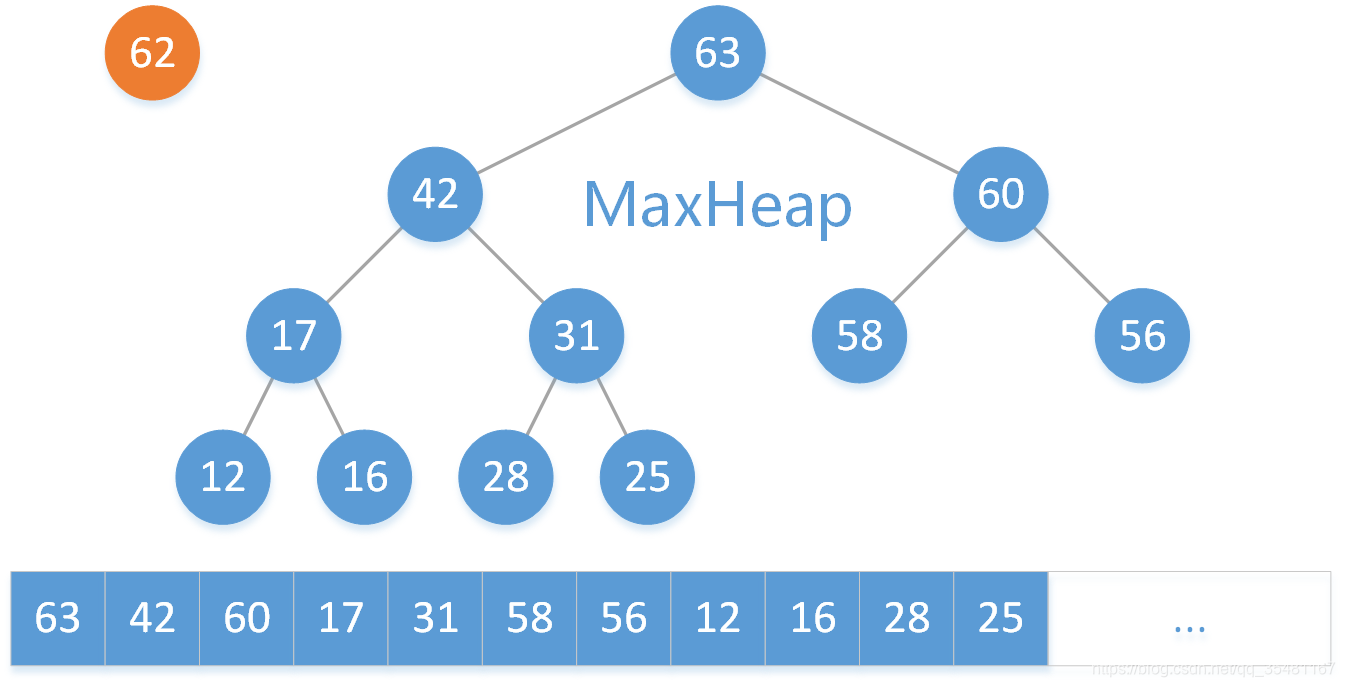
我們有這樣最大二叉堆,下面表示的是陣列的實際存放位置。這時我們要將 62 這個元素放入陣列中。
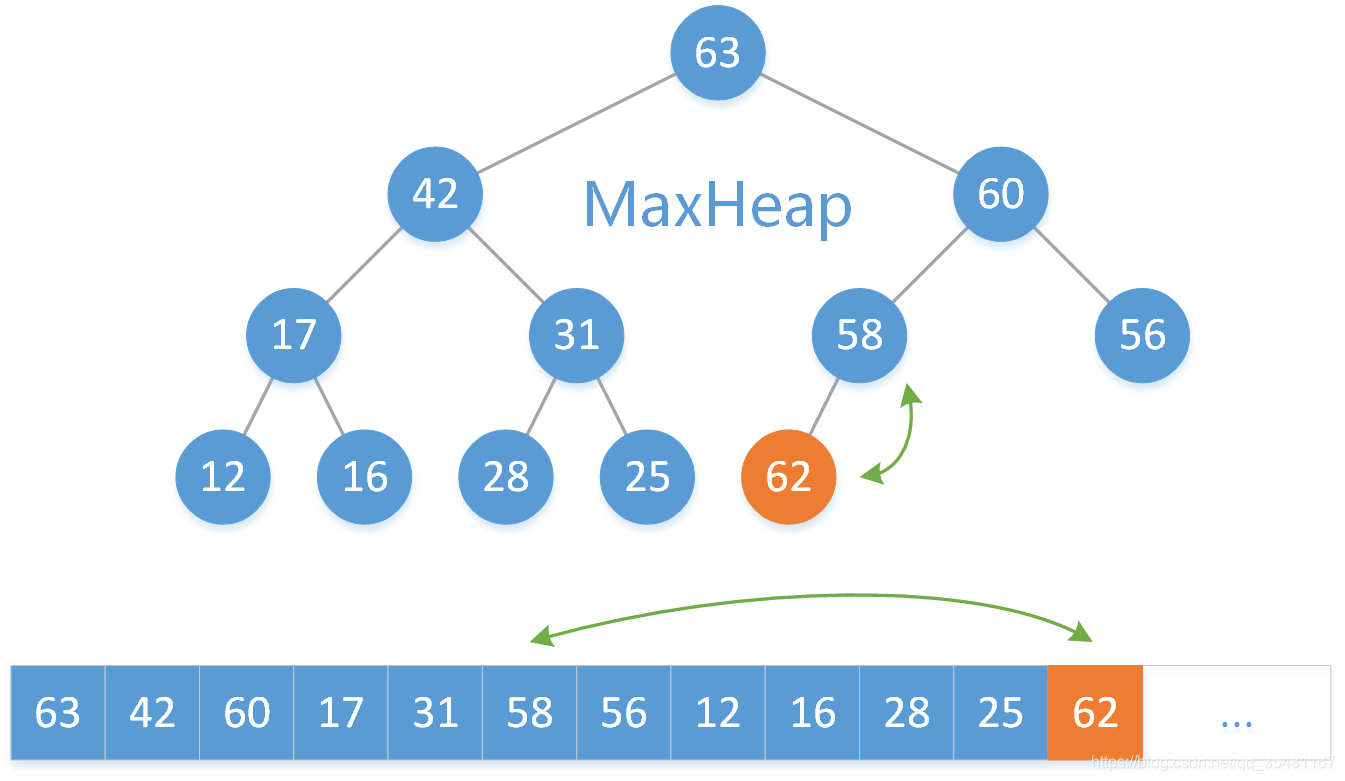
第一步:把 62 放到陣列的末尾。
第二步:找到 62 的父結點 58 ,因為 62 > 58 ,不滿足最大二叉堆的定義,所以交換 62 和 58 兩個元素。
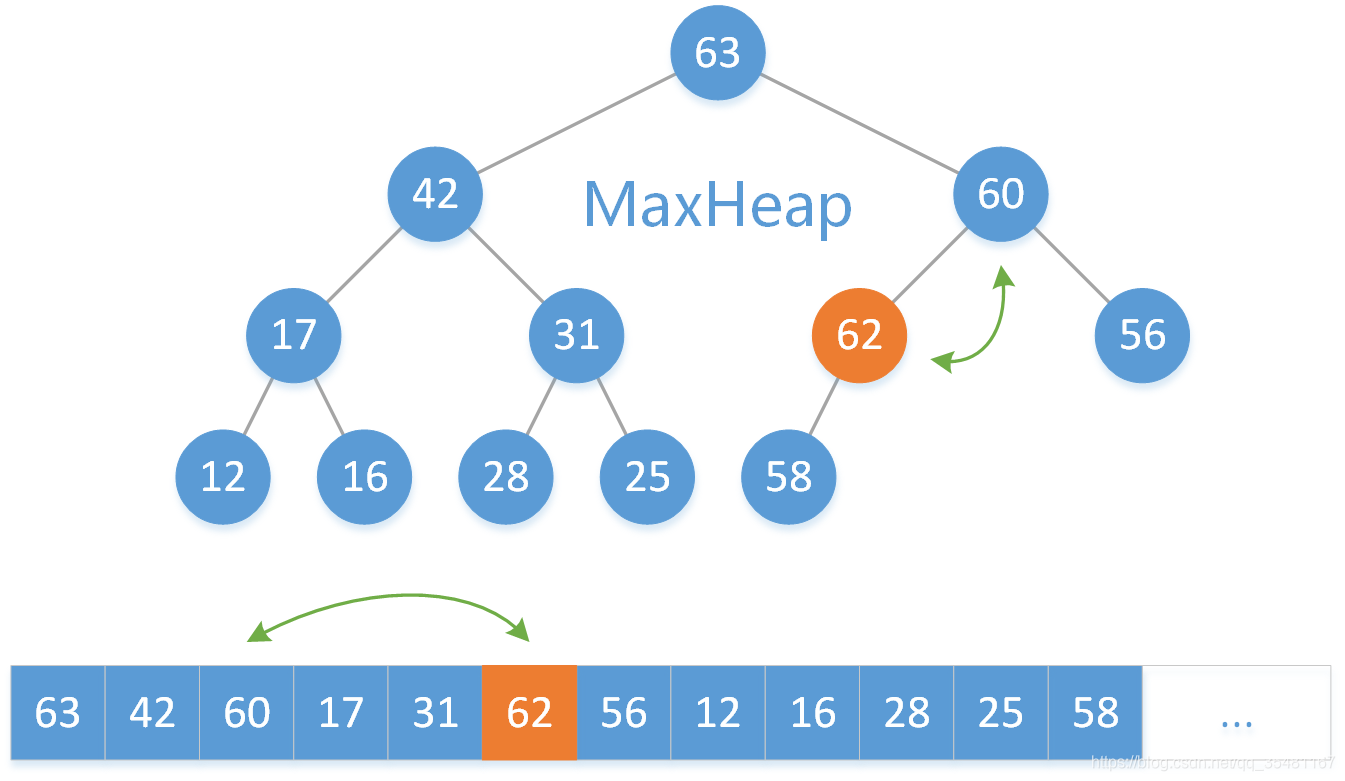
然後繼續將 62 與其父結點 60 比較,因為 62 > 60 ,所以交換 62 和 60 兩個元素。
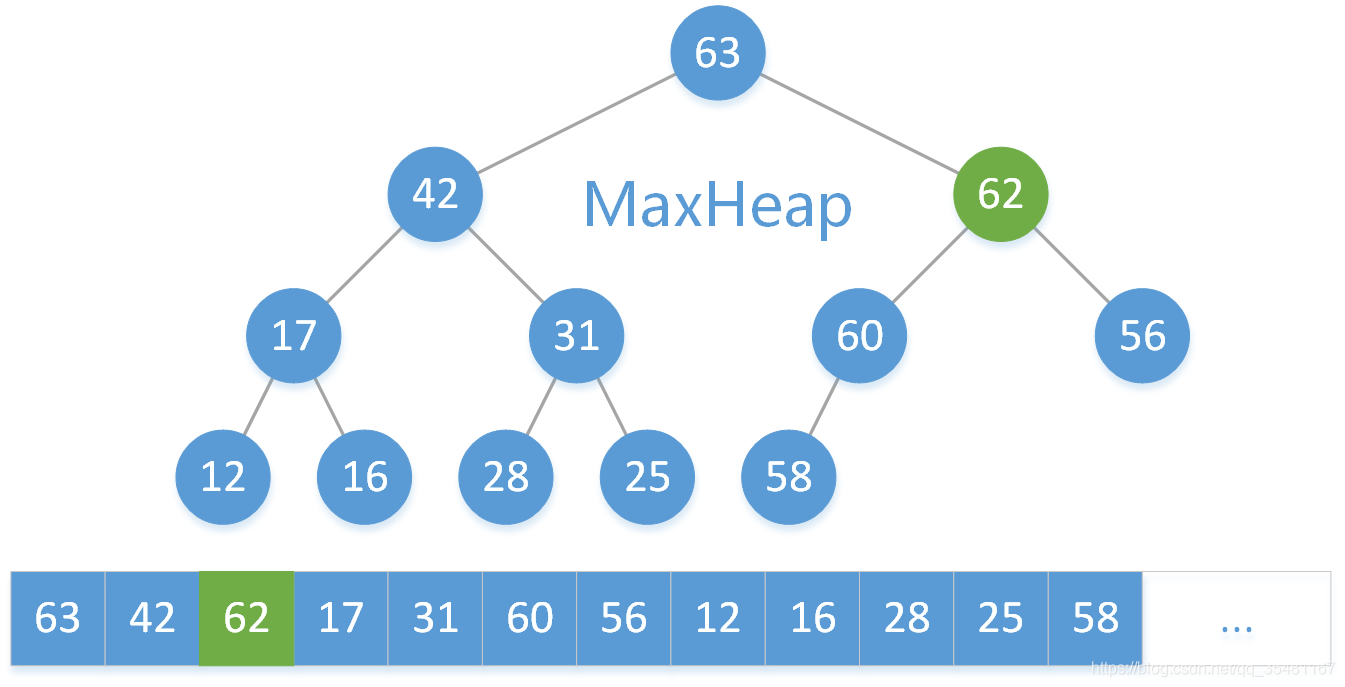
繼續將 62 與其父結點 63 比較,因為 62 < 63 ,滿足最大二叉堆定義,所以增加操作結束。
通過上面的例項,我們發現,除了陣列的增加操作之外,還需要一個逐步交換元素的函式,我們稱之為 上浮(siftUp),具體程式碼如下:
template <class T>
class MaxHeap{
...
private:
...
void siftUp(int index){
while (index && arr.get(index) > arr.get(parent(index))){
swap(index, parent(index));
index = parent(index);
}
}
...
};
這裡為了交換方便,編寫了一個 swap 函式 ,當然,這個函式也可以定義在陣列內部。
template <class T>
class MaxHeap{
...
private:
...
void swap(int i, int j){
if (i < 0 || i >= arr.size() || j < 0 || j >= arr.size()){
return;
}
T t = arr.get(i);
arr.set(i, arr.get(j));
arr.set(j, t);
}
...
};
有了 siftUp 函式,增加操作就變得很簡單了。
template <class T>
class MaxHeap{
public:
...
void add(T num){
arr.addLast(num);
siftUp(arr.size() - 1);
}
...
};
由於底層是動態陣列,所以不需要考慮記憶體方面的問題。
2.2 刪除操作
同樣,對於最大二叉堆的刪除操作,我們也是先從邏輯結構上進行推理,然後利用陣列去實現。
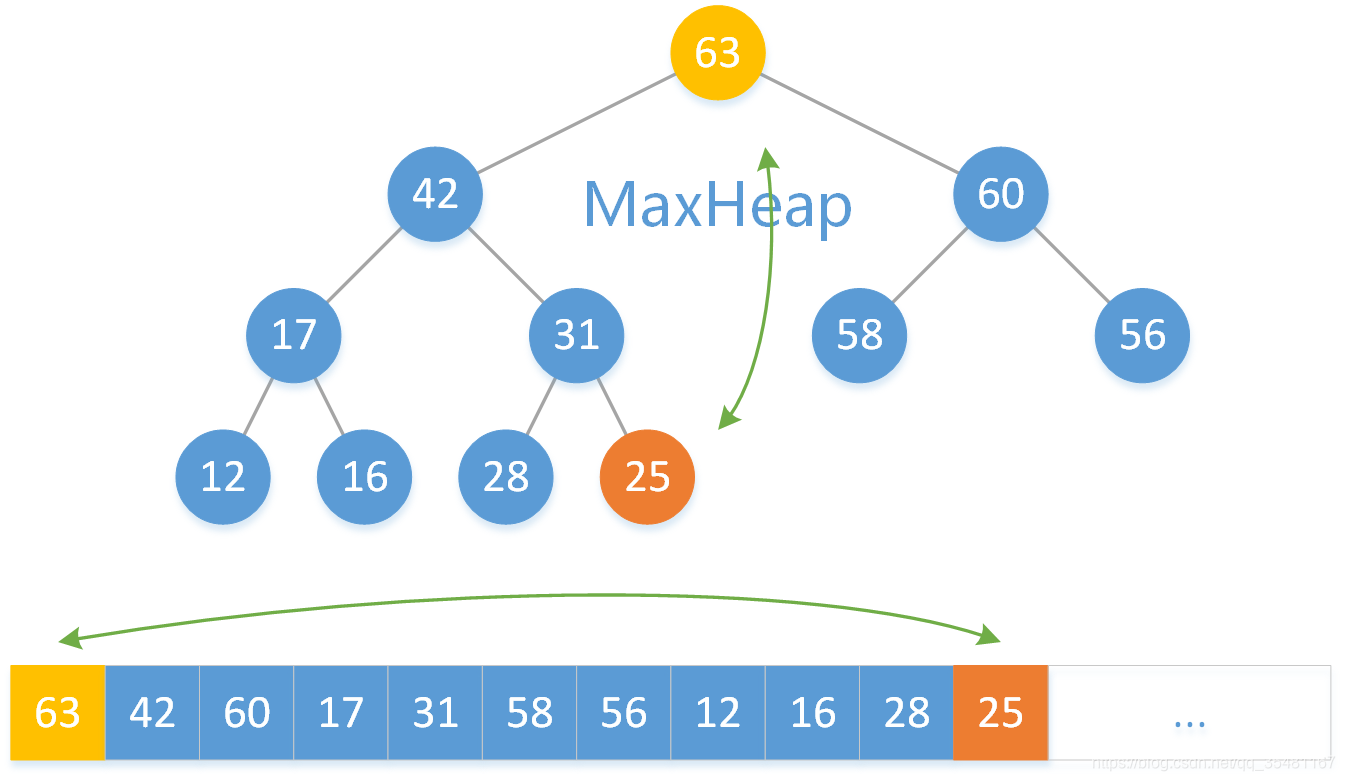
我們要取出最大二叉堆的最大的元素,即根結點元素,而陣列操作針對陣列末尾操作比較方便,所以現將陣列的首尾元素交換。
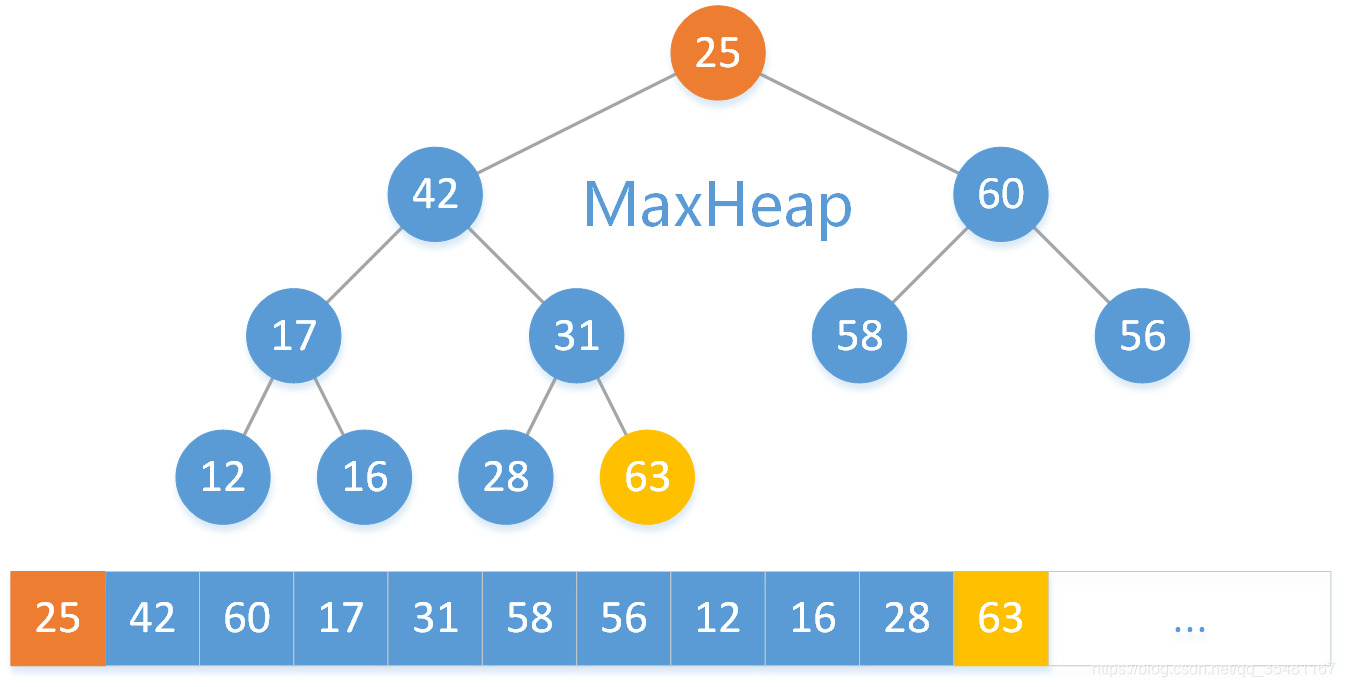
刪除掉陣列的最後一個元素。
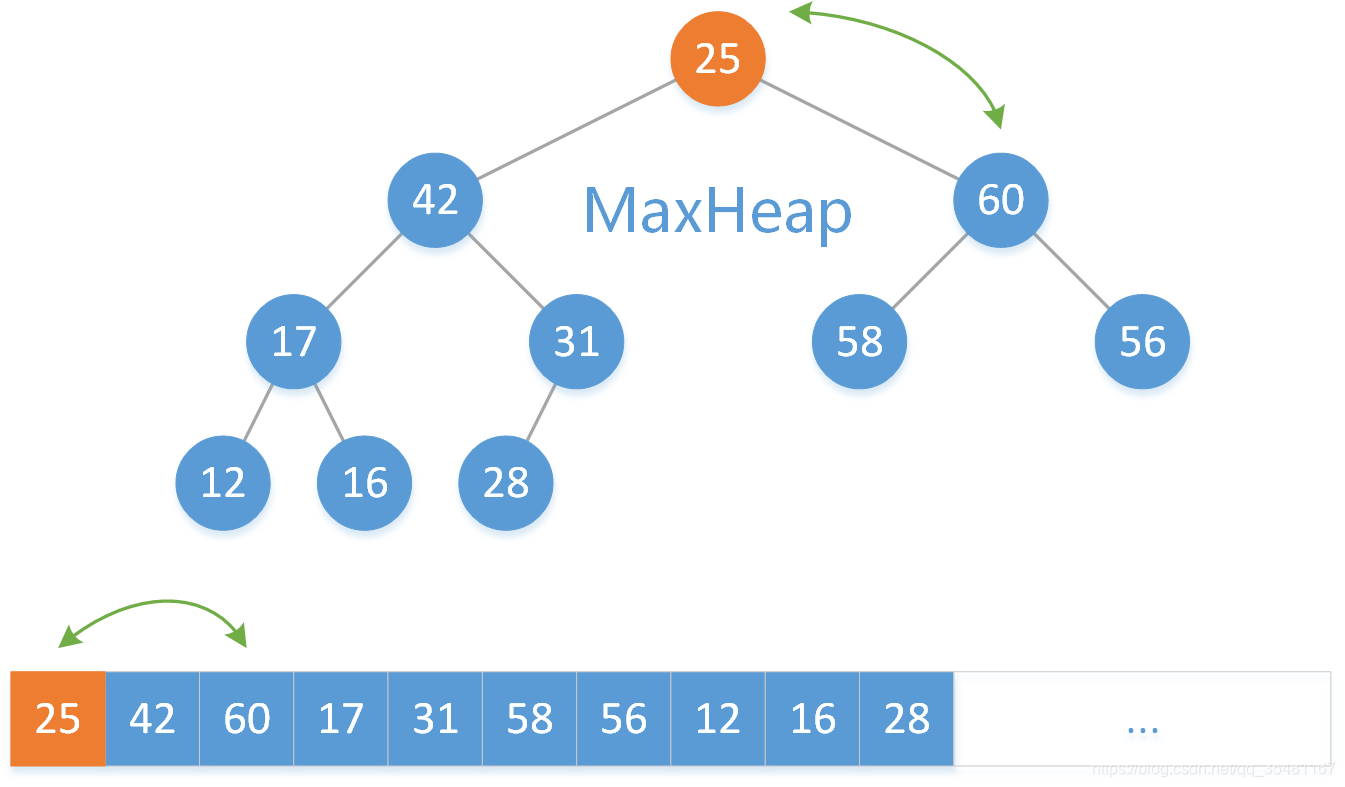
此時根結點是原來陣列尾端元素,所以需要判斷其位置是否合理。將 25 與其左右子結點元素比較大的那個 60 相比較,25 < 60 ,所以將 25 和 60 交換。
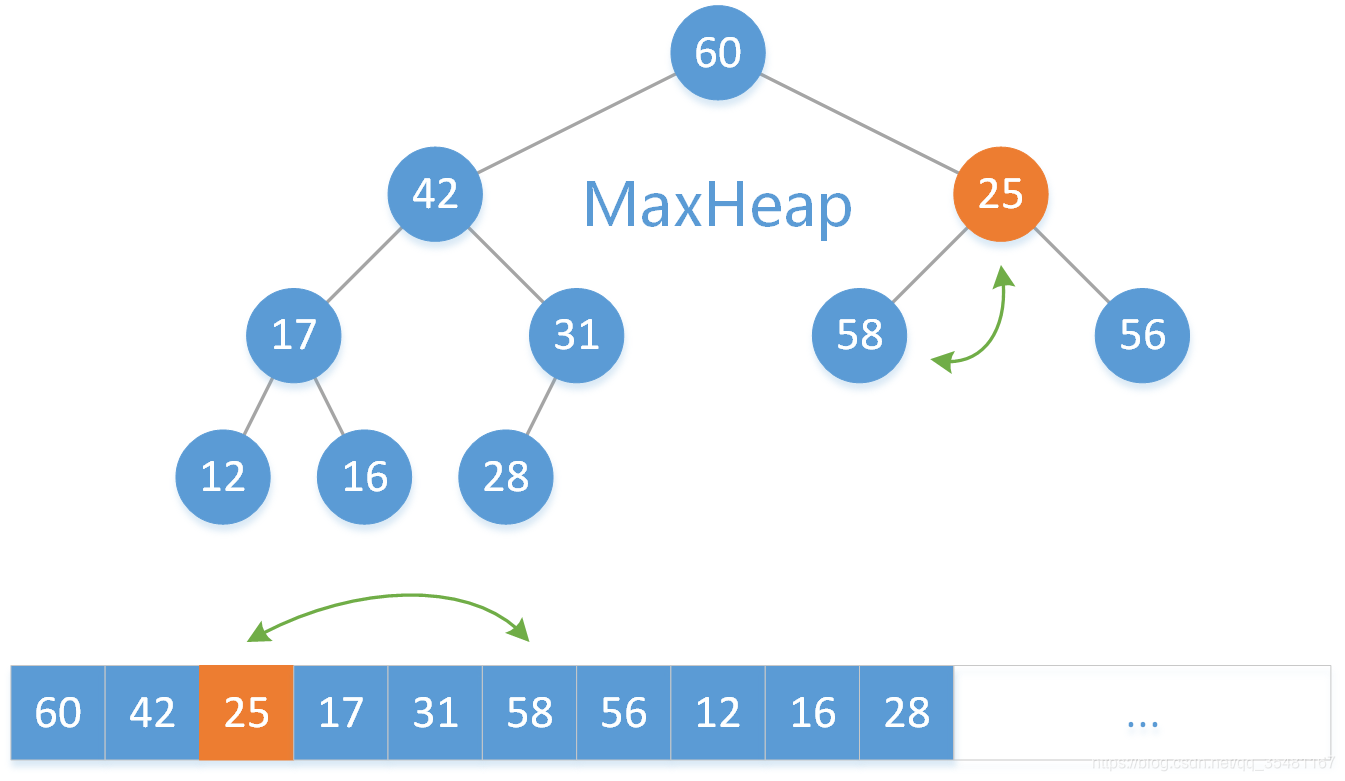
繼續把 25 和其左右子結點元素較大的 58 相比,25 < 58 ,所以將 25 和 58 交換。
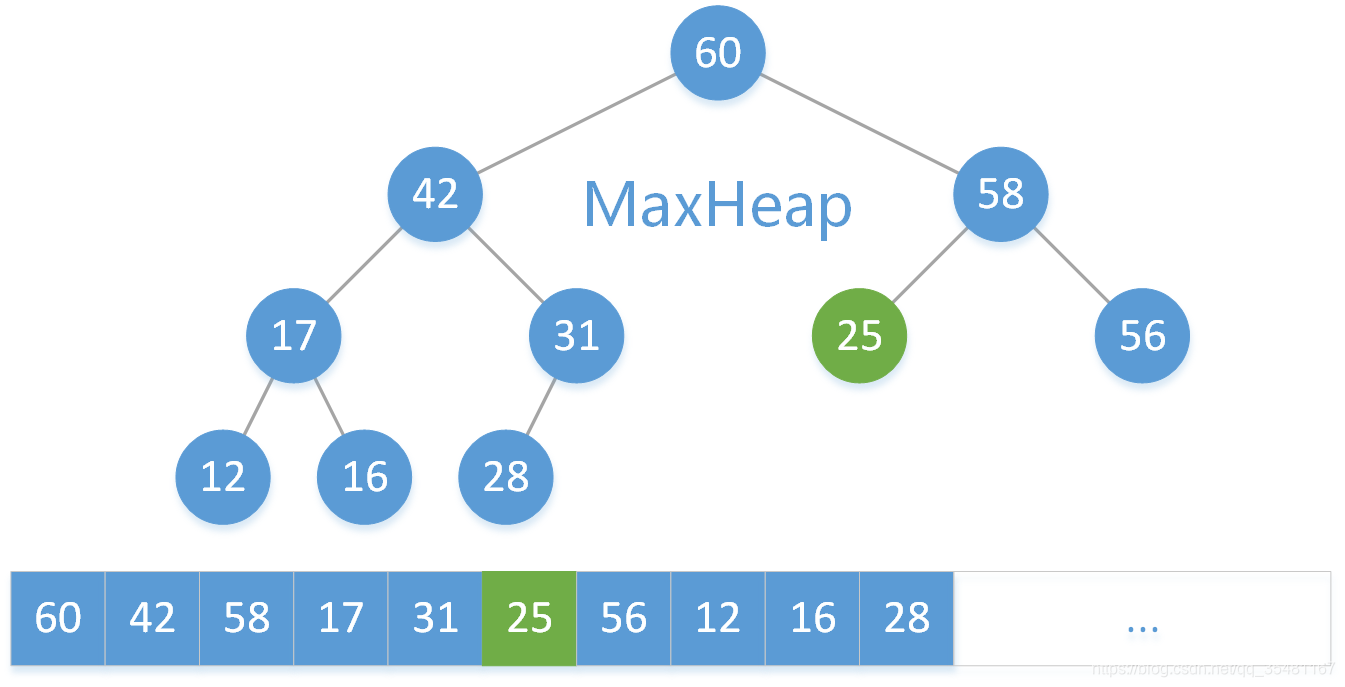
這時,25 的左右子結點均為空,刪除操作結束。
與增加操作類似,需要一個逐步交換元素的函式,我們稱之為 下沉(siftDown),具體程式碼如下:
template <class T>
class MaxHeap{
...
private:
...
void siftDown(int index){
while (leftChild(index) < arr.size()){
int left = leftChild(index);
if (left + 1 < arr.size() && arr.get(left + 1) > arr.get(left)){
left++;
}
if (arr.get(index) >= arr.get(left)){
break;
}
swap(index, left);
index = left;
}
}
...
};
相應的刪除函式如下:
template <class T>
class MaxHeap{
public:
...
T extractMax(){
T res = findMax();
swap(0, arr.size() - 1);
arr.removeLast();
siftDown(0);
return res;
}
...
};
2.3 查詢操作
最大二叉堆的查詢比較簡單,只能查到根結點(即最大的那個元素)。
template <class T>
class MaxHeap{
...
T findMax(){
if (arr.size() == 0){
cout << "二叉堆為空!" << endl;
return NULL;
}
return arr.get(0);
}
...
};
2.4 其他操作
最大二叉堆還有一些其他的操作,包括 二叉堆大小 等的查詢操作。
template <class T>
class MaxHeap{
public:
int size(){
return arr.size();
}
bool isEmpty(){
return arr.isEmpty();
}
...
};
3. 演算法複雜度分析
3.1 增加操作
| 函式 | 最壞複雜度 | 平均複雜度 |
|---|---|---|
| add | O(logn) | O(logn) |
add 的最壞複雜度 O(n+n) 中第一個 n 是指元素移動操作,第二個 n 是指 resize 函式,以下同理。
增加可能會引發擴容操作,平均而言,每增加 n 個元素,會擴充套件一次,會發生 n 個元素的移動,所以平均下來是 O(1) 。
3.2 刪除操作
| 函式 | 最壞複雜度 | 平均複雜度 |
|---|---|---|
| extractMax | O(logn) | O(logn) |
同理,刪除操作與增加操作類似。
3.3 查詢操作
| 函式 | 最壞複雜度 | 平均複雜度 |
|---|---|---|
| findMax | O(1) | O(1) |
總體情況:
| 操作 | 時間複雜度 |
|---|---|
| 增 | O(logn) |
| 刪 | O(logn) |
| 查 | O(1) |
由此可以看出,二叉堆操作的時間複雜度相較陣列而言更小。
4. 完整程式碼
最大二叉堆介面函式一覽:
| 函式宣告 | 函式型別 | 函式功能 |
|---|---|---|
| int size() | public | 返回二叉堆的大小 |
| bool isEmpty() | public | 返回二叉堆是否為空(空返回true) |
| void add(T) | public | 向二叉堆新增元素 |
| T findMax() | public | 返回二叉堆中最大元素 |
| T extractMax() | public | 取出二叉堆最大元素並返回該元素 |
| int parent(int) | private | 返回某索引對應結點父結點索引 |
| int leftChild(int) | private | 返回某索引對應結點左子結點索引 |
| int rightChild(int) | private | 返回某索引對應結點右子結點索引 |
| void swap(int,int) | private | 交換二叉堆中兩元素 |
| void siftUp(int) | private | 將二叉堆中某索引元素上浮 |
| void siftDown(int) | private | 將二叉堆中某索引元素下沉 |
程式完整程式碼(這裡使用了標頭檔案的形式來實現類)如下:
注:動態陣列 類程式碼不再贅述,如有需要參見 1.1 。
#ifndef __MAXHEAP_H__
#define __MAXHEAP_H__
#include "Array.h"
template <class T>
class MaxHeap{
public:
int size(){
return arr.size();
}
bool isEmpty(){
return arr.isEmpty();
}
void add(T num){
arr.addLast(num);
siftUp(arr.size() - 1);
}
T findMax(){
if (arr.size() == 0){
cout << "二叉堆為空!" << endl;
return NULL;
}
return arr.get(0);
}
T extractMax(){
T res = findMax();
swap(0, arr.size() - 1);
arr.removeLast();
siftDown(0);
return res;
}
private:
int parent(int index){
if (index <= 0 || index >= arr.size()){
return NULL;
}
return (index - 1) / 2;
}
int leftChild(int index){
return index * 2 + 1;
}
int rightChild(int index){
return (index + 1) * 2;
}
void swap(int i, int j){
if (i < 0 || i >= arr.size() || j < 0 || j >= arr.size()){
return;
}
T t = arr.get(i);
arr.set(i, arr.get(j));
arr.set(j, t);
}
void siftUp(int index){
while (index && arr.get(index) > arr.get(parent(index))){
swap(index, parent(index));
index = parent(index);
}
}
void siftDown(int index){
while (leftChild(index) < arr.size()){
int left = leftChild(index);
if (left + 1 < arr.size() && arr.get(left + 1) > arr.get(left)){
left++;
}
if (arr.get(index) >= arr.get(left)){
break;
}
swap(index, left);
index = left;
}
}
private:
Array<T> arr;
};
#endif
