資料結構實現 10.1:AVL樹(C++版)
資料結構實現 10.1:AVL樹(C++版)
1. 概念及基本框架
AVL樹 (即自平衡樹)是一種二分搜尋樹,AVL 樹要求每個結點的左右子樹的樹高度差不超過 1 。
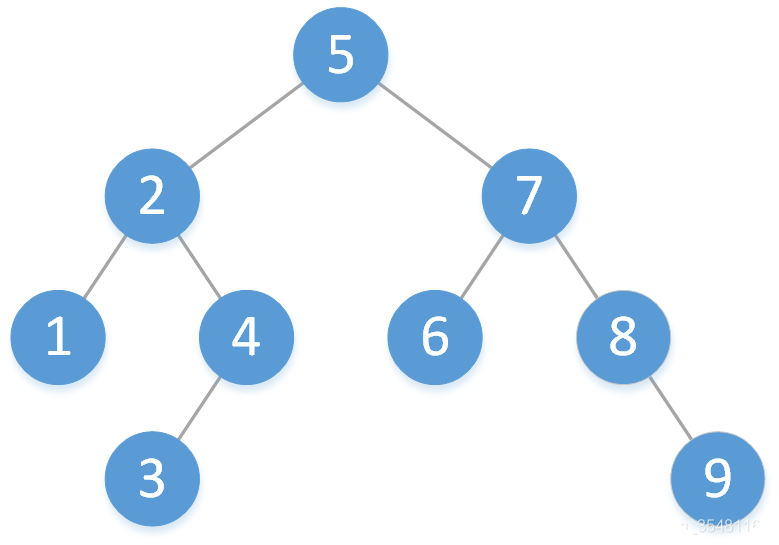
因為在二分搜尋樹中,不管二叉樹左右子樹的高度,所以二分搜尋樹的最壞情況可以退化成連結串列。所以這裡我們需要對二分搜尋樹進行適當的修正,提高效率。
與二分搜尋樹類似,我們先給出AVL樹的結點類:
template <typename K, typename V> 這裡我們增加了高度變數,用來記錄每個結點的當前高度。
下面給出AVL樹大體框架:
template < 與二分搜尋樹十分類似,所以這裡不再贅述。
接下來我們就對AVL樹的增加、刪除、查詢、遍歷以及一些其他基本操作用程式碼去實現。
2. 基本操作程式實現
2.1 增加操作
既然AVL樹是二分搜尋樹的一種,所以其基本實現程式碼與二分搜尋樹類似,我們直接給出:
template <typename K, typename V>
class AVLTree{
public:
...
//增加操作
void add(K key, V value);
...
private:
AVLNode<K, V>* add(AVLNode<K, V>* node, K key, V value);
...
};
類外實現程式碼:
template <typename K, typename V>
void AVLTree<K, V>::add(K key, V value){
root = add(root, key, value);
}
template <typename K, typename V>
AVLNode<K, V>* AVLTree<K, V>::add(AVLNode<K, V>* node, K key, V value){
if (node == NULL){
m_size++;
return new AVLNode<K, V>(key, value);
}
else if (key < node->key){
node->left = add(node->left, key, value);
}
else if (key > node->key){
node->right = add(node->right, key, value);
}
else if (key == node->key){
node->value = value;
return node;
}
//計算平衡因子
node->height = max(getHeight(node->left), getHeight(node->right)) + 1;
int balanceFactor = getBalanceFactor(node);
//平衡維護
if (balanceFactor > 1 && getBalanceFactor(node->left) >= 0){
return rightRotate(node);
}
else if (balanceFactor < -1 && getBalanceFactor(node->right) <= 0){
return leftRotate(node);
}
else if (balanceFactor > 1 && getBalanceFactor(node->left) < 0){
node->left = leftRotate(node->left);
return rightRotate(node);
}
else if (balanceFactor < -1 && getBalanceFactor(node->right) > 0){
node->right = rightRotate(node->right);
return leftRotate(node);
}
return node;
}
這裡需要注意的是在進行完增加操作之後我們需要進行一定的修正。修正之前需要得到一些基礎資訊,用下面幾個函式來實現。
max 返回其中的最大值。
getHeight 返回一個結點的高度。
getBalanceFactor 返回一個結點的平衡因子。(用左子樹高度減去右子樹高度)
leftRotate、rightRotate 分別表示左旋、右旋,具體實現方法後面詳細講述。
前面三個函式程式碼如下:
template <typename K, typename V>
class AVLTree{
...
private:
...
int max(int a, int b){ return a > b ? a : b; }
...
};
template <typename K, typename V>
int AVLTree<K, V>::getHeight(AVLNode<K, V>* node){
if (node == NULL){
return 0;
}
return node->height;
}
template <typename K, typename V>
int AVLTree<K, V>::getBalanceFactor(AVLNode<K, V>* node){
int lHeight = 0, rHeight = 0;
if (node == NULL){
return 0;
}
if (node->left != NULL){
lHeight = node->left->height;
}
if (node->right != NULL){
rHeight = node->right->height;
}
return lHeight - rHeight;
}
接下來我們詳細講述修正的左旋和右旋函式。
首先我們分情況,當一個新增加的結點需要修正,一定是其祖父結點一脈單傳到了新結點。那麼,作為一個新增加的結點,有兩種可能,在父結點的左/右,而父結點也可以在祖父節點的左/右,所以一共有四種。我們可以簡稱為左左、左右、右左、右右四種情況。
2.1.1 左左
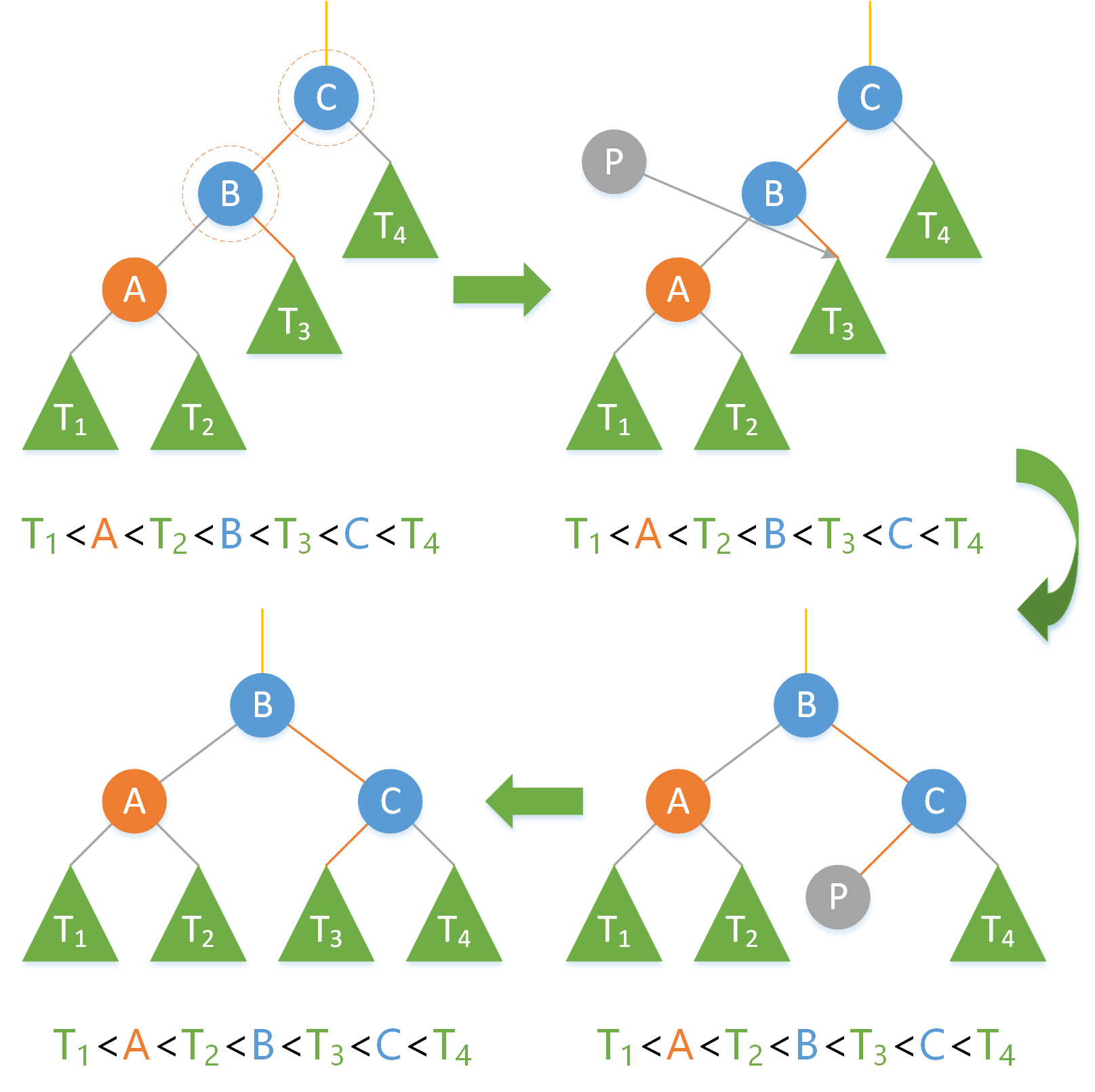
注:這裡每個結點都掛有子樹(子樹可以為空),這些子樹本身已經是平衡的了(下同,這裡考慮的是修正自下而上遞推到這裡),我們可以忽略。
如上圖,結點 C 左右子樹平衡因子為 2 > 1 ,所以需要修正,修正過程如下:
1.新建一個臨時結點 P 指向 B 的右子結點。
2.把 C 作為 B 的右子結點。
3.把 P 作為 C 的左子結點。
4.將結點 B 返回。
經過旋轉,結點的資料依舊滿足二分搜尋樹的基本性質,所以可以旋轉,這裡結點 B 和結點 C 發生了 右旋 。
圖中虛線圈住的結點表示實際發生了旋轉的結點,橙色(紫色)的線表示發生變化的支,黃色的線表示返回結點的指向,後面不再贅述。
右旋程式碼實現如下:
template <typename K, typename V>
AVLNode<K, V>* AVLTree<K, V>::rightRotate(AVLNode<K, V>* node){
AVLNode<K, V>* res = node->left;
AVLNode<K, V>* p = res->right;
res->right = node;
node->left = p;
//維護平衡
node->height = max(getHeight(node->left), getHeight(node->right)) + 1;
res->height = max(getHeight(res->left), getHeight(res->right)) + 1;
return res;
}
2.1.2 右右
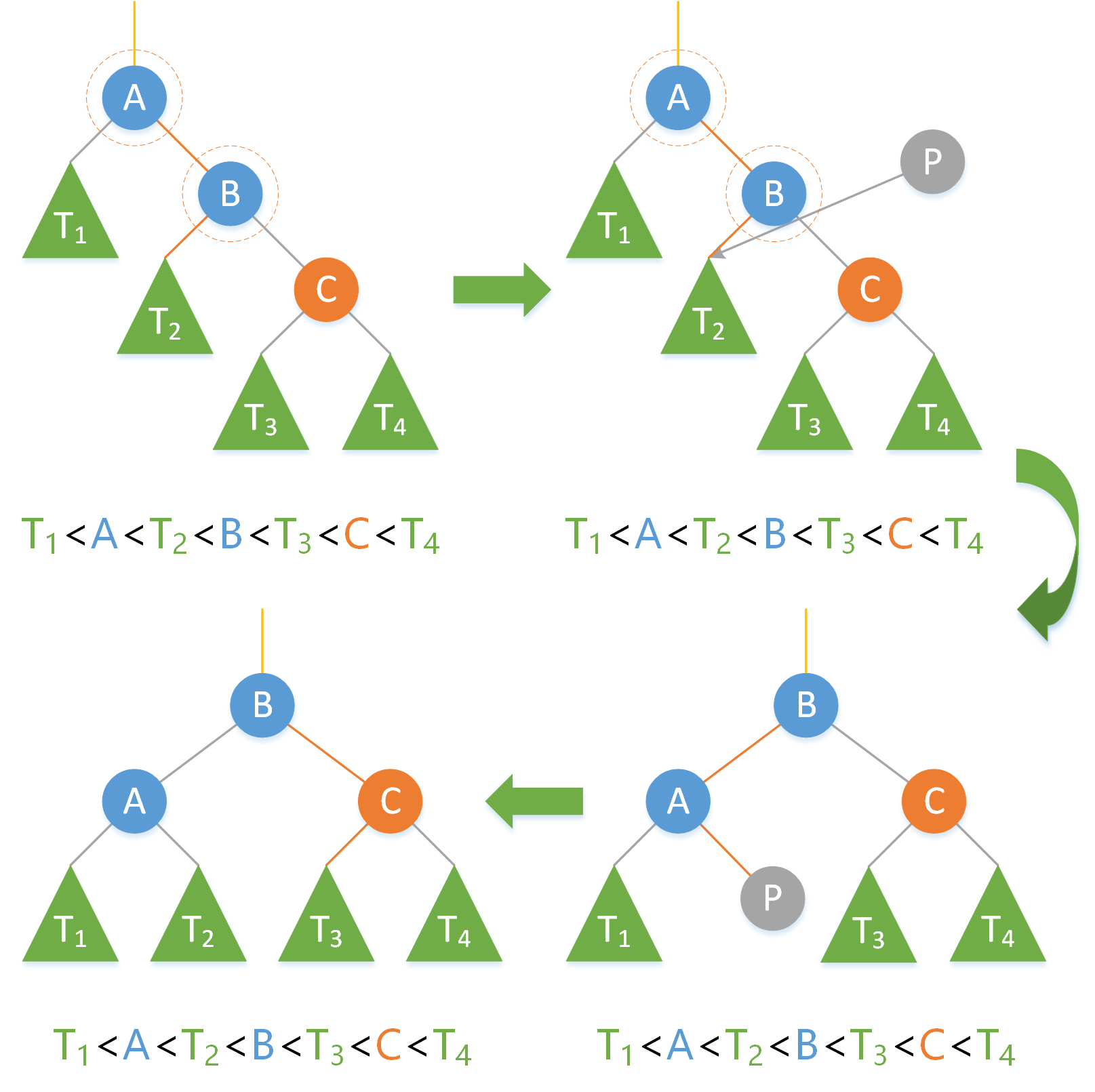
如上圖,結點 A 左右子樹平衡因子為 | - 2 | > 1 ,所以需要修正,修正過程如下:
1.新建一個臨時結點 P 指向 B 的左子結點。
2.把 A 作為 B 的左子結點。
3.把 P 作為 A 的右子結點。
4.將結點 B 返回。
經過旋轉,結點的資料依舊滿足二分搜尋樹的基本性質,所以可以旋轉,這裡結點 A 和結點 B 發生了 左旋 。
下面分析兩種比較複雜的情況,左右和右左。
左旋程式碼實現如下:
template <typename K, typename V>
AVLNode<K, V>* AVLTree<K, V>::leftRotate(AVLNode<K, V>* node){
AVLNode<K, V>* res = node->right;
AVLNode<K, V>* p = res->left;
res->left = node;
node->right = p;
//維護平衡
node->height = max(getHeight(node->left), getHeight(node->right)) + 1;
res->height = max(getHeight(res->left), getHeight(res->right)) + 1;
return res;
}
2.1.3 左右
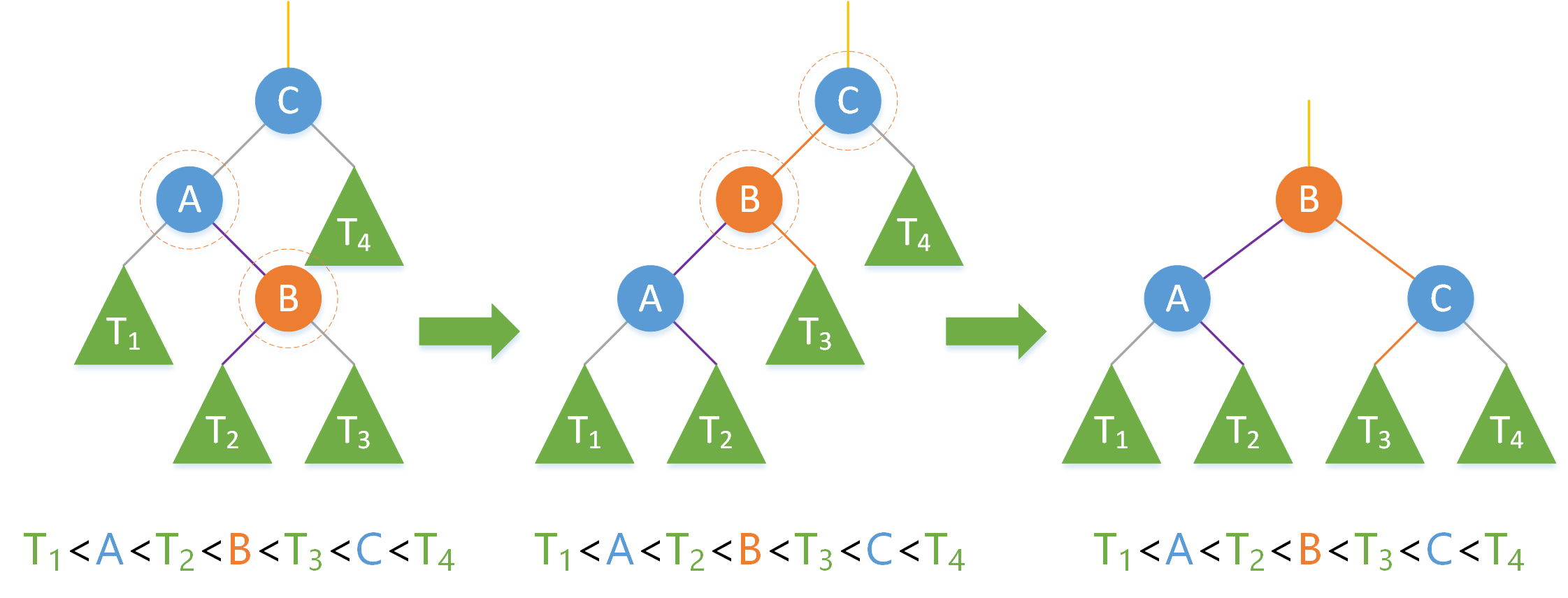
如上圖,結點 C 左右子樹平衡因子為 2 > 1 ,所以需要修正,修正過程如下:
1.把結點 A 和結點 B 左旋。(這時可看作右右情況)
2.把結點 B 和結點 C 右旋。(這時是左左情況)
3.返回結點 B 。
經過旋轉,結點的資料依舊滿足二分搜尋樹的基本性質。
2.1.4 右左
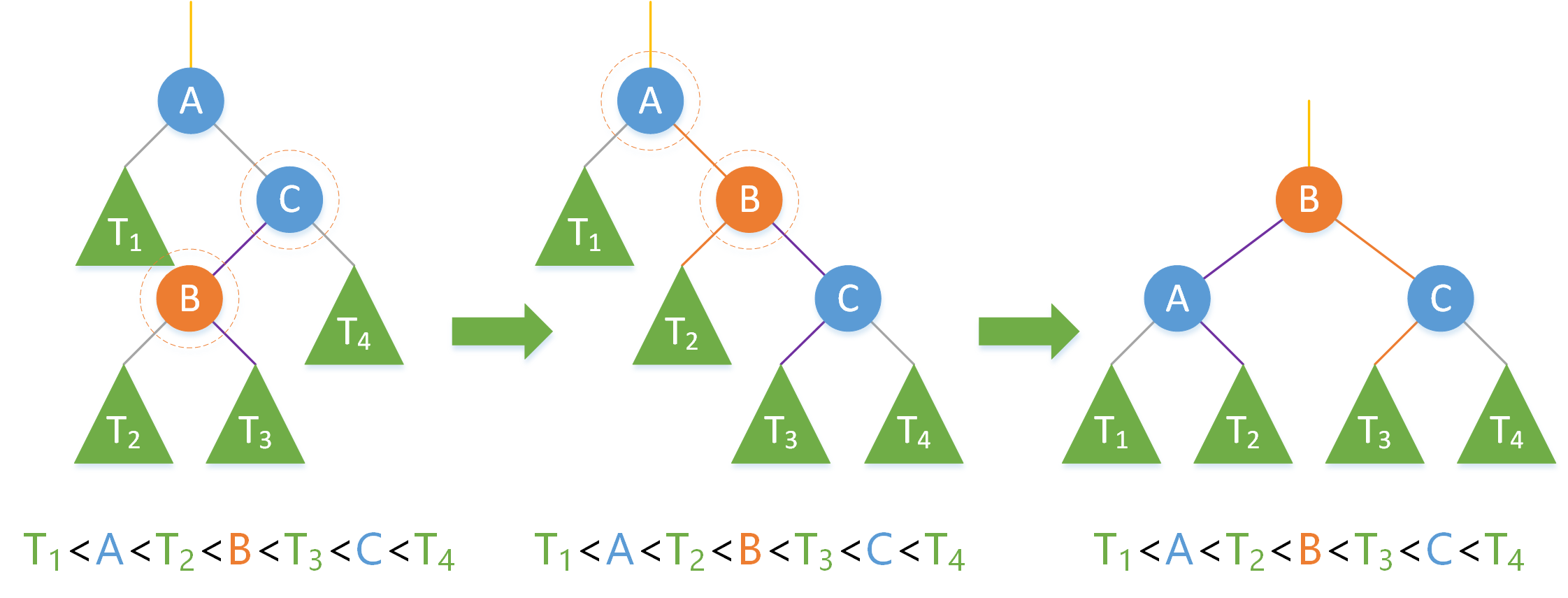
如上圖,結點 A 左右子樹平衡因子為 | - 2 | > 1 ,所以需要修正,修正過程如下:
1.把結點 B 和結點 C 右旋。(這時可看作左左情況)
2.把結點 A 和結點 B 左旋。(這時是右右情況)
3.返回結點 B 。
經過旋轉,結點的資料依舊滿足二分搜尋樹的基本性質。
2.1.5 增加操作修正總結
1.左左:右旋祖父結點和父結點,返回父結點。
2.右右:左旋祖父結點和父結點,返回父結點。
3.左右:左旋父結點和子結點,右旋祖父結點和新的父結點(即原來的子結點),返回新的父結點(即原來的子結點)。
4.右左:右旋父結點和子結點,左旋祖父結點和新的父結點(即原來的子結點),返回新的父結點(即原來的子結點)。
左左右,右右左,兄做侄,祖成兄,父替祖,返林中。
左右左,成左左,右左右,成右右,人雖新,法依舊。
2.2 刪除操作
刪除操作與二分搜尋樹類似,只是增加修正過程:
template <typename K, typename V>
class AVLTree{
public:
...
//刪除操作
void remove(K key);
...
private:
...
AVLNode<K, V>* remove(AVLNode<K, V>* node, K key);
...
};
類外實現如下:
template <typename K, typename V>
void AVLTree<K, V>::remove(K key){
root = remove(root, key);
}
template <typename K, typename V>
AVLNode<K, V>* AVLTree<K, V>::remove(AVLNode<K, V> *node, K key){
if (node == NULL){
return node;
}
AVLNode<K, V> *resNode = node;
if (key < node->key){
node->left = remove(node->left, key);
}
else if (key > node->key){
node->right = remove(node->right, key);
}
else if (key == node->key){
if (node->left == NULL){
AVLNode<K, V> *rightNode = node->right;
delete node;
m_size--;
resNode = rightNode;
}
else if (node->right == NULL){
AVLNode<K, V> *leftNode = node->left;
delete node;
m_size--;
resNode = leftNode;
}
else{
AVLNode<K, V> *minNode = node->right;
for (; minNode->left; minNode = minNode->left);
minNode->right = remove(node->right, minNode->key);
minNode->left = node->left;
node->left = node->right = NULL;
resNode = minNode;
}
}
if (resNode == NULL){
return NULL;
}
//計算平衡因子
resNode->height = max(getHeight(resNode->left), getHeight(resNode->right)) + 1;
int balanceFactor = getBalanceFactor(resNode);
//平衡維護
if (balanceFactor > 1 && getBalanceFactor(resNode->left) >= 0){
return rightRotate(resNode);
}
else if (balanceFactor < -1 && getBalanceFactor(resNode->right) <= 0){
return leftRotate(resNode);
}
else if (balanceFactor > 1 && getBalanceFactor(resNode->left) < 0){
resNode->left = leftRotate(resNode->left);
return rightRotate(resNode);
}
else if (balanceFactor < -1 && getBalanceFactor(resNode->right) > 0){
resNode->right = rightRotate(resNode->right);
return leftRotate(resNode);
}
return resNode;
}
2.2.1 左右均空

2.2.2 左空右不空
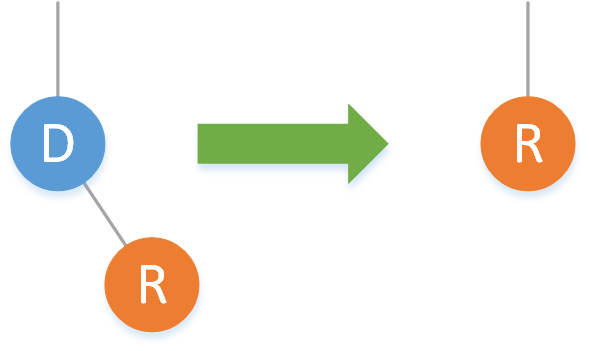
2.2.3 左不空右空
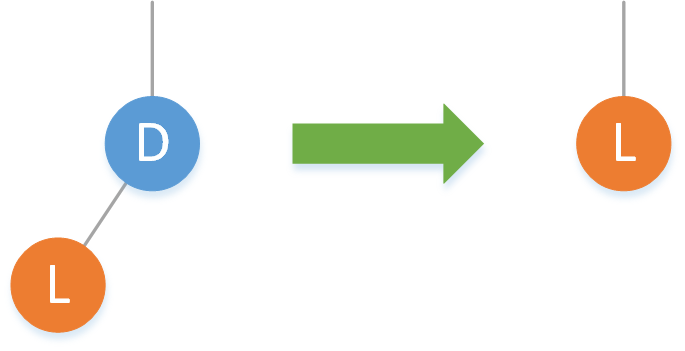
2.2.4 左右均不空
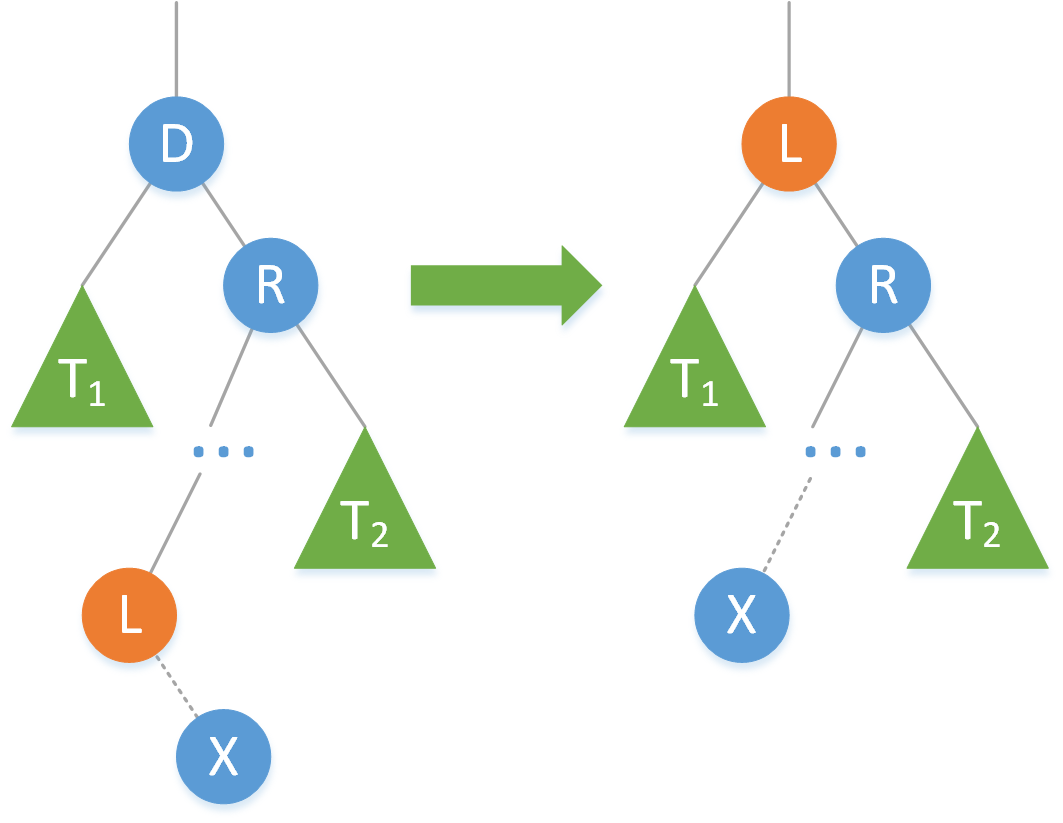
2.2.5 刪除操作修正總結
1.左右均空:直接刪除該結點,返回空。
2.左空右不空:刪除該結點,返回右子結點。
3.左不空右空:刪除該結點,返回左子結點。
4.左右均不空:找到該結點的右子結點的最左結點,即該結點的直接後繼,然後將該結點的值賦給要刪除的結點,然後刪掉這個後繼結點。
左子空,右子從,右子空,左子從,若無子,返作空。
尋右子,左子孫,無左子,方可停,假作真,除真身。
刪除後需要在刪除結點處開始維護平衡,方法同增加操作時的修正相同,這裡不再贅述。
2.3 查詢操作
這裡我們提供兩個查詢函式,contains 和 get ,函式實現程式碼如下。
template <typename K, typename V>
class AVLTree{
public:
...
//查詢操作
bool contains(K key);
V get(K key);
...
private:
...
bool contains(AVLNode<K, V>* node, K key);
...
};
類外實現如下:
template <typename K, typename V>
bool AVLTree<K, V>::contains(K key){
return contains(root, key);
}
template <typename K, typename V>
bool AVLTree<K, V>::contains(AVLNode<K, V> *node, K key){
if (node == NULL){
return false;
}
if (key == node->key){
return true;
}
else if (key < node->key){
return contains(node->left, key);
}
else{
return contains(node->right, key);
}
}
template <typename K, typename V>
V AVLTree<K, V>::get(K key){
AVLNode<K, V> *node = root;
while (node != NULL){
if (key == node->key){
return node->value;
}
else if (key < node->key){
node = node->left;
}
else if (key > node->key){
node = node->right;
}
}
cout << "查詢失敗!AVL樹中不存在" << key << "!" << endl;
return NULL;
}
2.4 遍歷操作
這裡與二分搜尋樹類似,所以只給出中序遍歷程式碼,其餘不再贅述。
template <typename K, typename V>
class AVLTree{
public:
...
//遍歷操作
void inOrder();
private:
...
void inOrder(AVLNode<K, V> *node);
...
};
類外實現如下:
template <typename K, typename V>
void AVLTree<K, V>::inOrder(){
cout << "AVL Tree: " << "Size = " << m_size << endl;
cout << "中序遍歷:";
inOrder(root);
cout << endl;
}
template <typename K, typename V>
void AVLTree<K, V>::inOrder(AVLNode<K, V> *node){
if (node == NULL)
