圖論學習(一)
阿新 • • 發佈:2018-11-27
圖論的發源
由著名的哥尼斯堡七橋問題引出,數學家尤拉將問題轉化為一個抽象圖形,如圖所示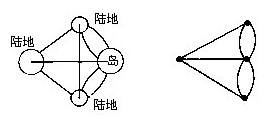
(問題的具體解法請自行百度 ^_^ )
由此開創了數學的一個新的分支——圖論與幾何拓撲,也由此展開了數學史上的新曆程。
圖的說明
圖的基本性質
圖graph :
圖中的一個點Vertex :
圖的邊edge :
例項:
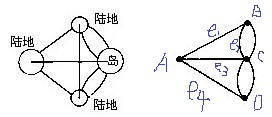
圖的寫法:
這裡的
2*{A,C}是因為A和C具有兩重邊。
圖的一些概念&定義
不同圖的定義:
- 簡單圖:不具有多重邊的圖。
- 多重圖:具有多重邊的圖。
點與點的關係:
- 鄰接:例如例項圖中,A和C有線連線,則稱AC是鄰接的
邊與點的關係:
- 關聯: 在例項圖中邊 關聯著A和C。
完全圖
定義
在圖論的數學領域,完全圖是一個簡單的無向圖,其中每對不同的頂點之間都恰連有一條邊相連。完整的有向圖又是一個有向圖,其中每對不同的頂點通過一對唯一的邊緣(每個方向一個)連線。(引用自百度百科)
圖的階數:完全圖中點的個數,以 表示。
圖的邊數:n個端點的完全圖有n個端點以及n(n − 1) / 2條邊,即
.
