基於演算法導論圖演算法-圖的建立

• 問題描述
• 問題分析
• 原始碼

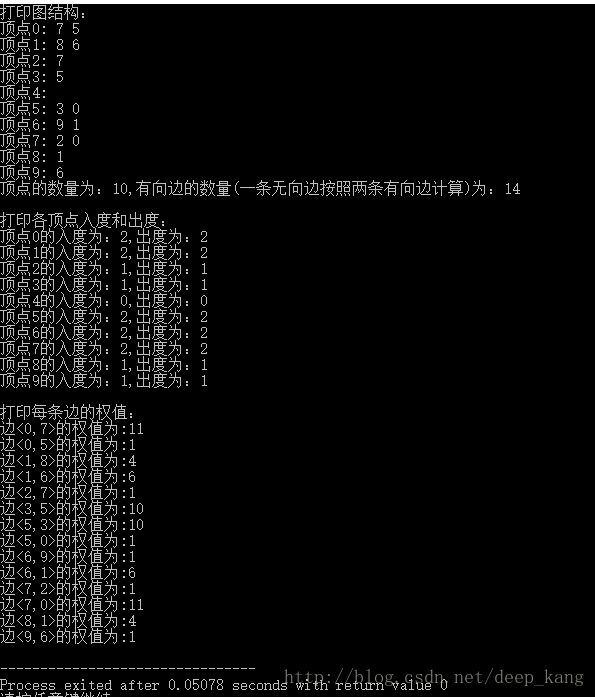
• 結果截圖

  問題描述

  隨機建立一個100個頂點，大約2000條邊的有向圖以及大約1000條邊的無向圖，並可以輸出每個點的入度和出度（使用鄰接表表示）

  問題分析

  本問題我通過首先建立一個隨機鄰接矩陣，並將其存入檔案中，然後從檔案中讀取資訊建立圖結構（與ACM題目吻合）

  難點在於圖的資料結構（我使用C/C++進行實現）

  原始碼

#pragma once
#include<iostream>
#include<ctime>
#include<cmath>
#include <cstdlib>
 

using namespace std;

typedef int Vertex;

struct Node;
typedef struct Node *PtrToNode, *List;
struct Node {
    Vertex    adjvex;
    int weight;
    PtrToNode next;//指向下一個結點的指標
};

struct VertexRecord {
    //ElementType  Element;
    int in_degree;//入度 
    int out_degree;//出度 
    List  adjto;//指向第一個鄰接結點的指標
 

};
struct GraphRecord {
    int      vexnum;
    struct VertexRecord *vertices;//陣列
};
typedef struct GraphRecord *Graph;

const int VertexNum = 20;
const int INF = 0x3f3f3f3f;

void CreateRandomDirectGraph();//生成有向圖的矩陣
Graph CreateDirectGraph();//根據隨機產生的有向圖矩陣生成有向圖的連結串列表示
void CreateRandomUndirectGraph();//生成有向圖的矩陣
 

Graph CreateUndirectGraph();//根據隨機產生的有向圖矩陣生成有向圖的連結串列表示
void print_graph(Graph G);//列印圖結構
void print_VertexDegree(Graph G);//列印圖各頂點的度數
void print_EdgeWeight(Graph G);//列印圖的各邊的權值

int matrix[VertexNum + 1][VertexNum + 1];
double random(double start, double end);
double random(double start, double end)//產生start~end之間的隨機數 
{
    return start + (end - start)*rand() / (RAND_MAX + 1.0);
}

void CreateRandomDirectGraph()
{   
    FILE *fp;
    fp = fopen("F:/C++/DirectGraph_100.txt", "w");
    srand(unsigned(time(0)));
    int x;
    for (int i = 0; i < VertexNum;i++) {
        for (int j = 0; j < VertexNum; j++) {
            x = (int)random(0, 20);//產生0~20的隨機數，如果小於5則有邊（題目要求20個頂點，大約100條邊）
            if (i!=j&&x < 5) matrix[i][j] = 1;
            else matrix[i][j] = 0;
            fprintf(fp,"%d\n", matrix[i][j]);
        }
    }
    fclose(fp);
}

Graph CreateDirectGraph() {
    FILE *fp;
    fp = fopen("F:/C++/DirectGraph_100.txt", "r");
    //圖的初始化 
    Graph G;
    PtrToNode ptr;
    G = (struct GraphRecord*)malloc(sizeof(struct GraphRecord));
    G->vexnum = VertexNum;
    G->vertices = (struct VertexRecord*)malloc(sizeof(struct VertexRecord)*VertexNum);
    for (int i = 0; i < VertexNum; i++) {
        G->vertices[i].adjto = NULL;
        G->vertices[i].in_degree = 0;
        G->vertices[i].out_degree = 0;
    }

    int flag;
    srand(unsigned(time(0)));
    int Edge_weight;
    //圖的構建 
    for (int i = 0; i < VertexNum; i++) {
        for (int j = 0; j < VertexNum; j++) {
            fscanf(fp, "%d", &flag);
            if (flag) {
                Edge_weight = (int)random(1, 20);//隨機產生邊的權值 
                ptr = (struct Node*)malloc(sizeof(struct Node));
                ptr->adjvex = j;
                ptr->weight = Edge_weight;
                G->vertices[i].out_degree++;//出度
                G->vertices[j].in_degree++;//入度
                ptr->next = G->vertices[i].adjto;
                G->vertices[i].adjto = ptr;
            }
        }
    }
    fclose(fp);
    return G;
}

void CreateRandomUndirectGraph()//與creatRandomDirectGrap方法一致，隨機產生鄰接矩陣 
{
    FILE *fp;
    fp = fopen("F:/C++/UndirectGraph_100.txt", "w");
    srand(unsigned(time(0)));
    int x;
    for (int i = 0; i < VertexNum; i++) {
        for (int j = 0; j < VertexNum; j++) {
            x = (int)random(0, 20);
            if (i != j&&x < 5) matrix[i][j] = 1;
            else matrix[i][j] = 0;
            fprintf(fp, "%d\n", matrix[i][j]);
        }
    }
    fclose(fp);
}

Graph CreateUndirectGraph() {
    FILE *fp;
    fp = fopen("F:/C++/UndirectGraph_100.txt", "r");
    //圖的初始化 
    Graph G;
    PtrToNode ptr1, ptr2;
    G = (struct GraphRecord*)malloc(sizeof(struct GraphRecord));
    G->vexnum = VertexNum;
    G->vertices = (struct VertexRecord*)malloc(sizeof(struct VertexRecord)*VertexNum);
    for (int i = 0; i < VertexNum; i++) {
        G->vertices[i].adjto = NULL;
        G->vertices[i].in_degree = 0;
        G->vertices[i].out_degree = 0;
    }

    int flag;
    srand(unsigned(time(0)));
    int Edge_weight;

    //圖的構建 
    for (int i = 0; i < VertexNum; i++) {
        for (int j = i + 1; j < VertexNum; j++) {
            fscanf(fp, "%d", &flag);
            if (flag) {
                Edge_weight = (int)random(1, 20);//隨機產生邊的權值 
                ptr1 = (struct Node*)malloc(sizeof(struct Node));
                ptr1->adjvex = j;
                ptr1->weight = Edge_weight;
                G->vertices[i].out_degree++;//出度
                G->vertices[j].in_degree++;//入度
                ptr1->next = G->vertices[i].adjto;
                G->vertices[i].adjto = ptr1;

                ptr2 = (struct Node*)malloc(sizeof(struct Node));
                ptr2->adjvex = i;
                ptr2->weight = Edge_weight;
                G->vertices[j].out_degree++;//出度
                G->vertices[i].in_degree++;//入度
                ptr2->next = G->vertices[j].adjto;
                G->vertices[j].adjto = ptr2;

            }
        }
    }
    fclose(fp);
    return G;
}

void print_graph(Graph G) {//列印圖結構 
    PtrToNode ptr;
    int count = 0;
    for (int i = 0; i < G->vexnum; i++) {
        printf("頂點%d:", i);
        ptr = G->vertices[i].adjto;
        while (ptr != NULL) {
            printf(" %d", ptr->adjvex);
            ptr = ptr->next;
            count++;
        }
        printf("\n");
    }
    printf("頂點的數量為：%d,有向邊的數量(一條無向邊按照兩條有向邊計算)為：%d\n", VertexNum, count);
}

void print_VertexDegree(Graph G) {
    for (int i = 0; i < G->vexnum; i++) {
        printf("頂點%d的入度為：%d,出度為：%d\n", i, G->vertices[i].in_degree, G->vertices[i].out_degree);
    }
}

void print_EdgeWeight(Graph G) {
    PtrToNode ptr;
    for (int i = 0; i < G->vexnum; i++) {
        ptr = G->vertices[i].adjto;
        while (ptr != NULL) {
            printf("邊<%d,%d>的權值為:%d\n", i,ptr->adjvex, ptr->weight);
            ptr = ptr->next;
        }
    }
}

int main() {
    //有向圖的隨機生成（20個頂點，100左右的邊，可以進行修改）
    //CreateRandomDirectGraph();
    //Graph G = CreateDirectGraph();

    //無向邊的隨機生成（20個頂點，50左右的邊）
    CreateRandomUndirectGraph();
    Graph G = CreateUndirectGraph();

    print_graph(G);//列印圖
    printf("列印各頂點入度和出度：\n");
    print_VertexDegree(G);//列印頂點度數
    printf("列印每條邊的權值：\n");
    print_EdgeWeight(G);//列印邊權

    return 0;   
} 

• 結果截圖（為了展示全貌，減少頂點數和邊數進行展示）