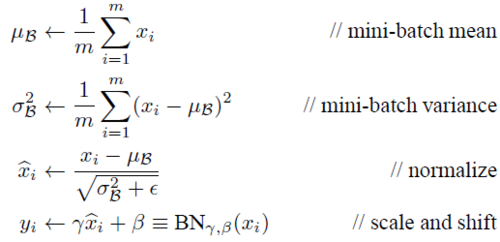BN 簡介

背景

批標準化（Batch Normalization ）簡稱BN演算法，是為了克服神經網路層數加深導致難以訓練而誕生的一個演算法。根據ICS理論，當訓練集的樣本資料和目標樣本集分佈不一致的時候，訓練得到的模型無法很好的泛化。

而在神經網路中，每一層的輸入在經過層內操作之後必然會導致與原來對應的輸入訊號分佈不同,,並且前層神經網路的增加會被後面的神經網路不對的累積放大。這個問題的一個解決思路就是根據訓練樣本與目標樣本的比例對訓練樣本進行一個矯正，而BN演算法（批標準化）則可以用來規範化某些層或者所有層的輸入，從而固定每層輸入訊號的均值與方差。

使用方法

批標準化一般用在非線性對映（啟用函式）之前，對y= Wx + b

在神經網路收斂過慢或者梯度爆炸時的那個無法訓練的情況下都可以嘗試

優點

• 減少了引數的人為選擇,可以取消dropout和L2正則項引數,或者採取更小的L2正則項約束引數
• 減少了對學習率的要求
• 可以不再使用區域性響應歸一化了,BN本身就是歸一化網路(區域性響應歸一化-AlexNet)
• 更破壞原來的資料分佈,一定程度上緩解過擬合

計算公式

其過程類似於歸一化但是又不同.

參考

BN原理的詳細參考建議:BN學習筆記:點選這裡

BN with TF

組成部分

BN在TensorFlow中主要有兩個函式:tf.nn.moments

tf.nn.moments

TensorFlow中的函式

moments(
    x,
    axes,
    shift=None,
    name=None,
    keep_dims=False
)

  Returns:
    Two `Tensor` objects: `mean` and `variance`.

其中引數 x 為要傳遞的tensor,axes是個int陣列,傳遞要進行計算的維度,返回值是兩個張量: mean and variance

# 計算Wx_plus_b 的均值與方差,其中axis = [0] 表示想要標準化的維度
img_shape= [128, 32, 32, 64]
Wx_plus_b = tf.Variable(tf.random_normal(img_shape))
axis = list(range(len(img_shape)-1)) # [0,1,2] 
wb_mean, wb_var = tf.nn.moments(Wx_plus_b, axis)

執行結果,因為初始的資料是隨機的,所以每次的執行結果並不一致:

*** wb_mean ***
[  1.05310767e-03   1.16801530e-03   4.95071337e-03  -1.50891789e-03
  -2.95298663e-03  -2.07848335e-03  -3.81800164e-05  -3.11688287e-03
   3.26496479e-03  -2.68524280e-04  -2.08893605e-03  -3.05374013e-03
   1.43721583e-03  -3.61034041e-03  -3.03616724e-03  -1.10225368e-03
   6.14093244e-03  -1.37914100e-03  -1.13333750e-03   3.53972078e-03
  -1.48577197e-03   1.04353309e-03   3.27868876e-03  -1.40919012e-03
   3.09609319e-03   1.98166977e-04  -5.25404140e-03  -6.03850756e-04
  -1.04614964e-03   2.90997117e-03   5.78491192e-04  -4.97420435e-04
   3.03052540e-04   2.46527663e-04  -4.70882794e-03   2.79057049e-03
  -1.98713480e-03   4.13944060e-03  -4.80978837e-04  -3.90357309e-04
   9.11145413e-04  -4.80215019e-03   6.26503082e-04  -2.76877987e-03
   3.79961479e-04   5.36157866e-04  -2.12549698e-03  -5.41620655e-03
  -1.93006988e-03  -8.54363534e-05   4.97094262e-03  -2.45843385e-03
   4.16610064e-03   2.44746287e-03  -4.15429426e-03  -6.64028199e-03
   2.56747357e-03  -1.63110415e-03  -1.53350492e-03  -7.66420271e-04
  -1.81624549e-03   2.16634944e-03   1.74984348e-03  -4.17272677e-04]
*** wb_var ***
[ 0.99813616  0.9983741   1.00014114  1.0012747   0.99496585  1.00168002
  1.00439012  0.99607879  1.00104094  0.99969071  1.01024568  0.99614906
  1.00092578  0.99977148  1.00447345  0.99580348  0.99797201  0.99119431
  1.00352168  0.9958936   0.99980813  1.00598109  1.00050855  0.99667317
  0.99352562  1.0036608   0.99794698  0.99324805  0.99862647  0.99930048
  0.99658304  1.00278556  0.99731135  1.00254881  0.99352133  1.00371397
  1.00258803  1.00388253  1.00404358  0.99454063  0.99434716  1.00087452
  1.00818515  1.00019705  0.99542576  1.00410056  0.99707311  1.00215423
  1.00199771  0.99394888  0.9973973   1.00197709  0.99835181  0.99944276
  0.99977624  0.99892712  0.99871159  0.99913275  1.00471914  1.00210452
  0.99568754  0.99547535  0.99983472  1.00523198]**重點內容**

我們已經假設圖片的shape[128, 32, 32, 64],它的運算方式如圖:

tf.nn.batch_normalization

TensorFlow中的函式

batch_normalization(
    x,
    mean,
    variance,
    offset,
    scale,
    variance_epsilon,
    name=None
)

其中x為輸入的tensor,mean,variance由moments()求出,而offset,scale一般分別初始化為0和1,variance_epsilon一般設為比較小的數字即可,參考程式碼如下:

scale = tf.Variable(tf.ones([64]))
offset = tf.Variable(tf.zeros([64]))
variance_epsilon = 0.001
Wx_plus_b = tf.nn.batch_normalization(Wx_plus_b, wb_mean, wb_var, offset, scale, variance_epsilon)

# 根據公式我們也可以自己寫一個
Wx_plus_b1 = (Wx_plus_b - wb_mean) / tf.sqrt(wb_var + variance_epsilon)
Wx_plus_b1 = Wx_plus_b1 * scale + offset
# 因為底層運算方式不同,實際上自己寫的最後的結果與直接呼叫tf.nn.batch_normalization獲取的結果並不一致

執行結果,因為初始的資料是隨機的,所以每次的執行結果並不一致,但是本例子中的計算差異始終存在:

# 這裡我們只需比較前兩的矩陣即可發現存在的數值差異
[[[[  3.32006335e-01  -1.00865233e+00   4.68401730e-01 ...,
     -1.31523395e+00  -1.13771069e+00  -2.06656289e+00]
   [  1.92613199e-01  -1.41019285e-01   1.03402412e+00 ...,
      1.66336447e-01   2.34183773e-01   1.18540943e+00]
   [ -7.14844346e-01  -1.56187916e+00  -8.09686005e-01 ...,
     -4.23679769e-01  -4.32125211e-01  -3.35091174e-01]
   ..., 

[[[[  3.31096262e-01  -1.01013660e+00   4.63186830e-01 ...,
     -1.31972826e+00  -1.13898540e+00  -2.05973744e+00]
   [  1.91642866e-01  -1.42231822e-01   1.02848673e+00 ...,
      1.64460197e-01   2.32336998e-01   1.18214881e+00]
   [ -7.16206789e-01  -1.56353664e+00  -8.14172268e-01 ...,
     -4.26598638e-01  -4.33694094e-01  -3.33635926e-01]

完整的程式碼

# - * - coding: utf - 8 -*-
#
# 作者：田豐(FontTian)
# 建立時間:'2017/8/2'
# 郵箱：[email protected]
# CSDN：http://blog.csdn.net/fontthrone

import tensorflow as tf
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
# 計算Wx_plus_b 的均值與方差,其中axis = [0] 表示想要標準化的維度
img_shape = [128, 32, 32, 64]
Wx_plus_b = tf.Variable(tf.random_normal(img_shape))
axis = list(range(len(img_shape) - 1))
wb_mean, wb_var = tf.nn.moments(Wx_plus_b, axis)

scale = tf.Variable(tf.ones([64]))
offset = tf.Variable(tf.zeros([64]))
variance_epsilon = 0.001
Wx_plus_b = tf.nn.batch_normalization(Wx_plus_b, wb_mean, wb_var, offset, scale, variance_epsilon)

Wx_plus_b1 = (Wx_plus_b - wb_mean) / tf.sqrt(wb_var + variance_epsilon)
Wx_plus_b1 = Wx_plus_b1 * scale + offset

with tf.Session() as sess:
    tf.global_variables_initializer().run()

    print('*** wb_mean ***')
    print(sess.run(wb_mean))
    print('*** wb_var ***')
    print(sess.run(wb_var))
    print('*** Wx_plus_b ***')
    print(sess.run(Wx_plus_b))
    print('**** Wx_plus_b1 ****')
    print(sess.run(Wx_plus_b1))