PyTorch實現Pointer Networks
pytorch實現簡單的pointer networks
部分程式碼參照該GitHub以及該部落格。純屬個人模仿實驗。
- python3
- pytorch 0.4.0
Pointer Networks
Our model solves the problem of variable size output dictionaries using a recently proposed mechanism of neural attention. It differs from the previous attention attempts in that, instead of using attention to blend hidden units of an encoder to a context vector at each decoder step, it uses attention as a pointer to select a member of the input sequence as the output.——
[ Pointer Networks ]
個人理解Pointer Networks是attention的變體,attention是把encoder的所有輸出加權求和然後對映到輸出字典每個詞的概率,但這樣無法處理變長輸入的情況,最好我們希望將decoder某個時間步的輸出以及encoder所有輸出共同對映到輸入序列長度的概率分佈,這樣我們不光考慮了上下文(encoder所有輸出,類似attention),最主要的是我們得到了輸入序列相關位置的概率,即該模型充分考慮了輸入序列的位置資訊。確實,不同於句子,有些問題的輸入中每個元素之間可能是不相關的,傳統的seq2seq模型可能無法很好的解決。
資料格式
這裡我仿照寫了一段pointer networks的seq2seq模型,主要用來判斷一個序列數值大小起伏的邊界。邊界值有兩個,左邊一段元素都在1~5之間,中間一段元素值都在6~10之間,右邊一段元素值都在1~5之間,每段長度都在5~10之間,即兩個邊界點是不固定的。最大序列長度為30,不足用0填充,例如:
| input | target |
|---|---|
| [1,1,5,4,1,6,9,10,8,6,3,2,1] | [5, 9] |
| [2,3,4,1,4,3,7,8,6,7,9,10,6,2,5,4,2,4,1] | [6, 12] |
def generate_single_seq(length=30, min_len=5, max_len=10):
seq_before = [(random.randint(1, 5)) for x in range(random.randint(min_len, max_len))]
seq_during = [(random.randint(6, 10)) for x in range(random.randint(min_len, max_len))]
seq_after = [random.randint(1, 5) for x in range(random.randint(min_len, max_len))]
seq = seq_before + seq_during + seq_after
seq = seq + ([0] * (length - len(seq)))
return seq, len(seq_before), len(seq_before) + len(seq_during) - 1seq2seq模型
這裡我將encoder和decoder寫在了一起,decoder採用GRUCell迴圈計算目標序列長度次,訓練時每次用target作為decoder的輸入,測試時則用預測值作為輸入。注意每次計算的output被對映到了輸入序列長的概率(B, L)。
class PtrNet(nn.Module):
def __init__(self, input_dim, output_dim, embedding_dim, hidden_dim):
super().__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.embedding_dim = embedding_dim
self.hidden_dim = hidden_dim
self.encoder_embedding = nn.Embedding(input_dim, embedding_dim)
self.decoder_embedding = nn.Embedding(output_dim, embedding_dim)
self.encoder = nn.GRU(embedding_dim, hidden_dim)
self.decoder = nn.GRUCell(embedding_dim, hidden_dim)
self.W1 = nn.Linear(hidden_dim, hidden_dim, bias=False)
self.W2 = nn.Linear(hidden_dim, hidden_dim, bias=False)
self.v = nn.Linear(hidden_dim, 1, bias=False)
def forward(self, inputs, targets):
batch_size = inputs.size(1)
max_len = targets.size(0)
# (L, B)
embedded = self.encoder_embedding(inputs)
targets = self.decoder_embedding(targets)
# (L, B, E)
encoder_outputs, hidden = self.encoder(embedded)
# (L, B, H), (1, B, H)
# initialize
decoder_outputs = torch.zeros((max_len, batch_size, self.output_dim)).to(device)
decoder_input = torch.zeros((batch_size, self.embedding_dim)).to(device)
hidden = hidden.squeeze(0) # (B, H)
for i in range(max_len):
hidden = self.decoder(decoder_input, hidden)
# (B, H)
projection1 = self.W1(encoder_outputs)
# (L, B, H)
projection2 = self.W2(hidden)
# (B, H)
output = F.log_softmax(self.v(F.relu(projection1 + projection2)).squeeze(-1).transpose(0, 1), -1)
# (B, L)
decoder_outputs[i] = output
decoder_input = targets[i]
return decoder_outputs
def predict(self, inputs, max_trg_len):
batch_size = inputs.size(1)
# (L, B)
embedded = self.encoder_embedding(inputs)
# (L, B, E)
encoder_outputs, hidden = self.encoder(embedded)
# (L, B, H), (1, B, H)
# initialize
decoder_outputs = torch.zeros(max_trg_len, batch_size, self.output_dim).to(device)
decoder_input = torch.zeros((batch_size, self.embedding_dim)).to(device)
hidden = hidden.squeeze(0) # (B, H)
for i in range(max_trg_len):
hidden = self.decoder(decoder_input, hidden)
# (B, H)
projection1 = self.W1(encoder_outputs)
# (L, B, H)
projection2 = self.W2(hidden)
# (B, H)
a = self.v(F.relu(projection1 + projection2))
output = F.log_softmax(self.v(F.relu(projection1 + projection2)).squeeze(-1).transpose(0, 1), -1)
decoder_outputs[i] = output
_, indices = torch.max(output, 1)
decoder_input = self.decoder_embedding(indices)
return decoder_outputs測試結果
我用的訓練集9000,測試集1000。我同時比較了基本的seq2seq加不加attention的效果,發現基本的seq2seq難以收斂,甚至要迭代100~300個epoch才能到達較高的準確率。而pointer networks能夠迅速收斂,loss甚至能降為0,只要迭代20個epoch,準確率可以達到100%。loss結果如下,可以看出在第一個epoch,loss迅速下降,這是最明顯的不同。
epoch: 0 | total loss: 86.9745
epoch: 1 | total loss: 0.3416
epoch: 2 | total loss: 0.0915
epoch: 3 | total loss: 0.0412
epoch: 4 | total loss: 0.0231
epoch: 5 | total loss: 0.0147
epoch: 6 | total loss: 0.0101
epoch: 7 | total loss: 0.0073
epoch: 8 | total loss: 0.0055
epoch: 9 | total loss: 0.0043
epoch: 10 | total loss: 0.0034
epoch: 11 | total loss: 0.0028
epoch: 12 | total loss: 0.0023
epoch: 13 | total loss: 0.0019
epoch: 14 | total loss: 0.0016
epoch: 15 | total loss: 0.0014
epoch: 16 | total loss: 0.0012
epoch: 17 | total loss: 0.0010
epoch: 18 | total loss: 0.0009
epoch: 19 | total loss: 0.0008
epoch: 20 | total loss: 0.0007Acc: 100.00% (1000/1000)最後是3中模型loss在100個epoch的比較結果:
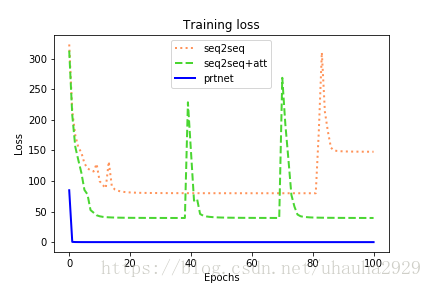
完整程式碼見這裡。
