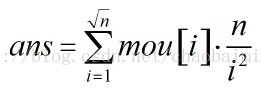題意：完全平方數是指含有平方數因子的數。求第ki個非完全平方數。

解法：比較明顯的二分，getsum(int middle)求1-middle有多少個非完全平方數，然後二分。求1-middle的非完全平方數個數可以用總數減掉完全平方數個數。計算完全平方數的個數用容斥：

    首先加上n/(2*2)+n/(3*3)+n/(5*5)+n/(7*7)...+...然後減掉出現兩次的，然後加上三次的...奇加偶減。這就是mou的原型，用mou陣列計算很簡單；

程式碼：

  

   

    
     
    
    
     
      /******************************************************
 

     
    
   

    
     
    
    
     
      * @author:xiefubao
     
    
   

    
     
    
    
     
      *******************************************************/
     
    
   

    
     
    
    
     
      #pragma comment(linker, "/STACK:102400000,102400000")
     
    
   

    
     
    
    
     
      #include
 
 <iostream>
     
    
   

    
     
    
    
     
      #include <cstring>
     
    
   

    
     
    
    
     
      #include <cstdlib>
     
    
   

    
     
    
    
     
      #include <cstdio>
     
    
   

    
     
    
    
     
      #include <queue>
 

     
    
   

    
     
    
    
     
      #include <vector>
     
    
   

    
     
    
    
     
      #include <algorithm>
     
    
   

    
     
    
    
     
      #include <cmath>
     
    
   

    
     
    
    
     
      #include <map>
     
    
   

    
     
    
    
     
      #include <set>
     
    
   

    
     
    
    
     
      #include <stack>
     
    
   

    
     
    
    
     
      #include <string.h>
     
    
   

    
     
    
    
     
      //freopen ("in.txt" , "r" , stdin);
     
    
   

    
     
    
    
     
      using 
      namespace 
      std;
     
    
   

    
     
    
    
      
     
    
   

    
     
    
    
     
      #define eps 1e-8
     
    
   

    
     
    
    
     
      #define zero(_) (abs(_)<=eps)
     
    
   

    
     
    
    
     
      const 
      double pi=
      acos(
      -1.0);
     
    
   

    
     
    
    
     
      typedef 
      unsigned 
      long 
      long LL;
     
    
   

    
     
    
    
     
      const 
      int Max=
      100010;
     
    
   

    
     
    
    
     
      const LL INF=
      2e16+
      7;
     
    
   

    
     
    
    
      
     
    
   

    
     
    
    
     
      LL mou[Max];
     
    
   

    
     
    
    
     
      void init()
     
    
   

    
     
    
    
     
      {
     
    
   

    
     
    
    
         
      for(LL i=
      2; i<Max; i++)
     
    
   

    
     
    
    
     
          {
     
    
   

    
     
    
    
             
      if(!mou[i])
     
    
   

    
     
    
    
     
              {
     
    
   

    
     
    
    
     
                  mou[i]=i;
     
    
   

    
     
    
    
                 
      for(LL j=i*i; j<Max; j+=i)
     
    
   

    
     
    
    
     
                      mou[j]=i;
     
    
   

    
     
    
    
     
              }
     
    
   

    
     
    
    
     
          }
     
    
   

    
     
    
    
     
          mou[
      1]=
      1;
     
    
   

    
     
    
    
         
      for(
      int i=
      2; i<Max; i++)
     
    
   

    
     
    
    
     
          {
     
    
   

    
     
    
    
             
      if(i/mou[i]%mou[i]==
      0) mou[i]=
      0;
     
    
   

    
     
    
    
             
      else mou[i]=-mou[i/mou[i]];
     
    
   

    
     
    
    
     
          }
     
    
   

    
     
    
    
     
      }
     
    
   

    
     
    
    
     
      int k;
     
    
   

    
     
    
    
     
      LL getnum(LL middle)
     
    
   

    
     
    
    
     
      {
     
    
   

    
     
    
    
     
          LL ans=
      0;
     
    
   

    
     
    
    
         
      for(LL i=
      1; i*i<=middle; i++)
     
    
   

    
     
    
    
     
          {
     
    
   

    
     
    
    
     
              ans+=mou[i]*(middle/(i*i));
     
    
   

    
     
    
    
     
          }
     
    
   

    
     
    
    
         
      return ans;
     
    
   

    
     
    
    
     
      }
     
    
   

    
     
    
    
     
      int main()
     
    
   

    
     
    
    
     
      {
     
    
   

    
     
    
    
     
          init();
     
    
   

    
     
    
    
         
      int t;
     
    
   

    
     
    
    
         
      cin>>t;
     
    
   

    
     
    
    
         
      while(t--)
     
    
   

    
     
    
    
     
          {
     
    
   

    
     
    
    
             
      scanf(
      "%d",&k);
     
    
   

    
     
    
    
     
              LL left=
      1,right=INF;
     
    
   

    
     
    
    
             
      while(left<=right)
     
    
   

    
     
    
    
     
              {
     
    
   

    
     
    
    
                 
      int middle=(left+right)/
      2;
     
    
   

    
     
    
    
                 
      if(getnum(middle)<k)
     
    
   

    
     
    
    
     
                      left=middle+
      1;
     
    
   

    
     
    
    
                 
      else
     
    
   

    
     
    
    
     
                      right=middle
      -1;
     
    
   

    
     
    
    
     
              }
     
    
   

    
     
    
    
             
      cout<<left<<
      '\n';
     
    
   

    
     
    
    
     
          }
     
    
   

    
     
    
    
         
      return 
      0;
     
    
   

    
     
    
    
     
      }