有一條直線段 $P_1P_2$，其端點座標分別是 $\mathrm{起}$

那麼這條直線段的引數表示式是：
$P(t)=P_1+(P_2-P_1)t=(1-t)P_1+tP_2 (0\leqslant t\leqslant1)$

這個式子怎麼理解呢？

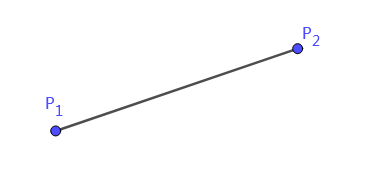
我們可以把 $P_1P_2$ 這條線段看作 100%，那麼該線段上任意一點到起始點 $P_1$ 的距離所佔 $P_1P_2$ 比例為 t， t 的大小在 [0, 1] 內。 $P_2-P_1$ 的含義就是沿著 $P_1P_2$ 直線段方向。

我對 t 一開始的推導如下：

不妨設 $P1(x_1, y_1)，P2(x_2,y_2)$，P1 和 P2 所在直線斜率為 $\alpha$.
則該直線引數方程為（可以參考我的 這篇文章）：
$\begin{cases} x=x_1+tcos\alpha \\& (t 是引數) \\ y = y_1 + tsin\alpha \end{cases}$
因此根據該引數方程我們可以繼續推導直線段的引數方程為
$(x, y)=(x_1,y_1)+(cos\alpha,sin\alpha)t$
而
$cos\alpha=\dfrac{x_2-x_1}{P1P2} \newline \newline sin\alpha=\dfrac{y_2-y_1}{P1P2}$
繼續推導可得：
$(x, y)=(x_1,y_1)+(x_2-x_1, y_2-y_1)\dfrac{t}{P1P2}$
而 t 的幾何含義是 |t| = |P1P2|
圖中 P(t) = P1 + (P2-P1)t 可以表示為：
$(x,y)=(x_1,y_1)+(x_2-x_1, y_2-y_1)t$
那麼為什麼圖片中的 t 的範圍是 [0, 1]?

這裡存在的問題就是直線段中兩個端點是確定的，而推導當中的直線引數方程中的一點是變化的。兩個的模型不同，因此不能這樣推導。