1.線性變換的實質

就是一個名字叫的好聽點的函式

2.為啥叫變換而不叫函式呢？

變換有運動之意。

3.變換與網格線

(1)線性變換

說明:白色網格線是原始的網格線，藍色的網格線是變換後的網格線。

(2)不知該怎麼稱呼的變換，反正不是線性變換

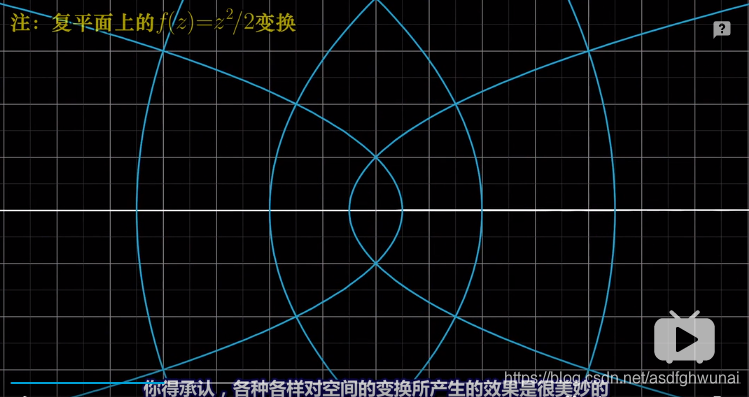
4.線性變換的定義

滿足兩條性質:

(1)直線依然是直線(更深的意思是變換後的網格線等距且平行分佈)；

(2)原點保持固定

下面倆不是線性變換

網格線不滿足平行且等距

原點被移動了

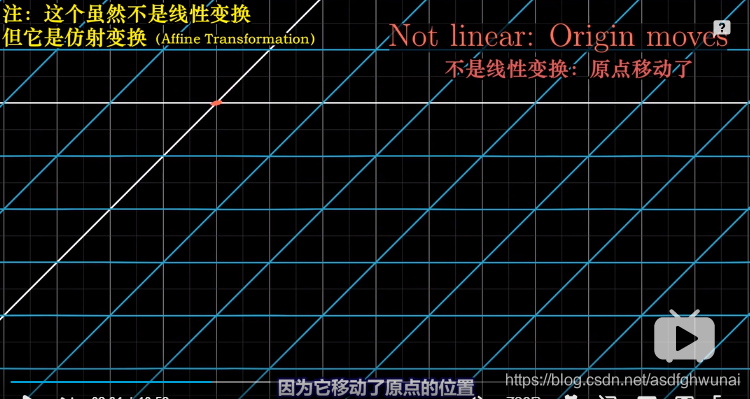
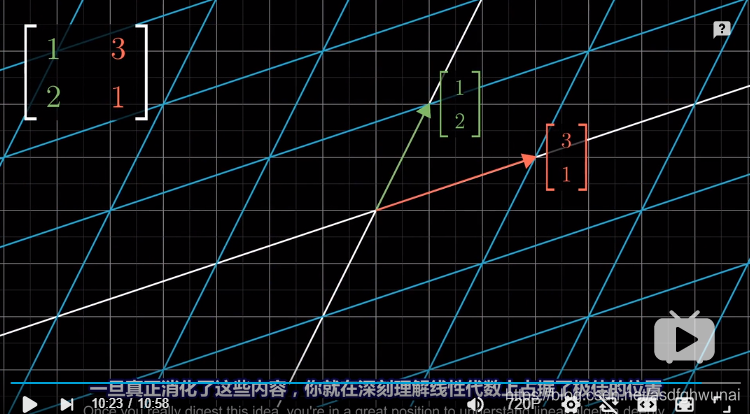
5.線性變換與基

只要知道變換後的基在哪，就可以直接推出變換後的向量在哪

6.誤區:矩陣的幾何意義

在二維空間中，線性變換是為了變換向量(描述物體的位置)，(a,c)和(b,d)是變換後的倆基向量,也就是線性變換方程組，而(x,y)是要變換的向量，(ax+by,cx+dy)是變換後的位置。

所以矩陣就是用於描述線性變換的，變換了原空間的位置(也即是向量描述)

當你看到矩陣，你就把他當成對空間的一種操作，第一列為第一個基，第二列為第二個基，扭曲了原空間

矩陣和向量那樣乘也是為了保持線性空間的特性

參考 https://www.bilibili.com/video/av6731067/?p=4