04 矩陣乘法與線性變換複合
矩陣相乘的幾何意義
矩陣相乘代表兩個線性變換的相繼作用
旋轉矩陣與剪下矩陣相乘 相當於 先旋轉再剪下

矩陣為啥那樣乘
第一步:
找出i基(0,1) 經過 第一次變換後 i基去哪了?

新的i基就是M1矩陣的第一列(e,g)
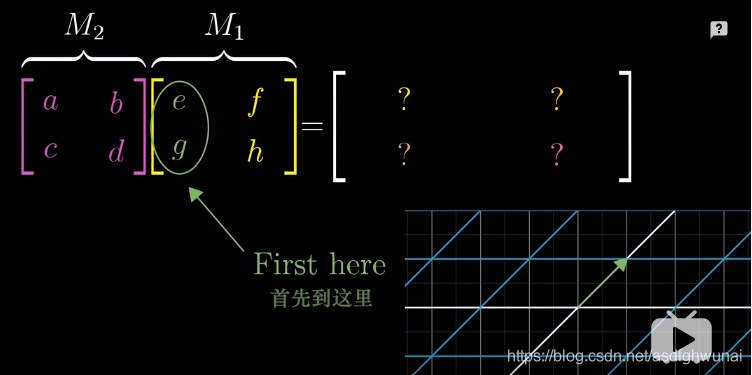
第二步:找出i基經過M2矩陣的變換後又到哪了?方法就是矩陣M2 和 i基 相乘

同理,j基(0,1) 經過M1和M2兩次變換後

相關推薦
04 矩陣乘法與線性變換複合
矩陣相乘的幾何意義 矩陣相乘代表兩個線性變換的相繼作用 旋轉矩陣與剪下矩陣相乘 相當於 先旋轉再剪下 矩陣為啥那樣乘 第一步: 找出i基(0,1) 經過 第一次變換後 i基去哪了? 新的i基就是M1矩陣的第一列(e,g)
03 矩陣與線性變換
1.線性變換的實質 就是一個名字叫的好聽點的函式 2.為啥叫變換而不叫函式呢? 變換有運動之意。 3.變換與網格線 (1)線性變換 說明:白色網格線是原始的網格線,藍色的網格線是變換後的網格線。 (2)不知該怎麼稱呼的變換,反正不是線性變換
MIT 線性代數導論 第三講:矩陣乘法與逆矩陣
為了以後自己看的明白(●’◡’●),我決定對複雜的計算過程不再用Latex插入數學公式了(記得不熟的實在是太費勁了,還是手寫好~) 第三講的主要內容有兩個: 四種矩陣乘法的方式 逆矩陣的概念以及計算方式 矩陣乘法(Matrix multiplication)
矩陣與線性變換
本文可以說是該系列最重要、最核心的文章。你對線性代數的一切困惑,根源就在於沒有真正理解矩陣到底是什麼。讀完咪博士的這篇文章,你一定會有一種醍醐灌頂、豁然開朗的感覺! 咱們先來說說啥叫變換。本質上,變換就是函式。 例如,你輸入一個向量 [57], 經過某個變換(即
線性代數的本質與幾何意義 03. 矩陣與線性變換 (3blue1brown 咪博士 圖文註解版)
首先,恭喜你讀到了咪博士的這篇文章。本文可以說是該系列最重要、最核心的文章。你對線性代數的一切困惑,根源就在於沒有真正理解矩陣到底是什麼。讀完咪博士的這篇文章,你一定會有一種醍醐灌頂、豁然開朗的感覺! 咱們先來說說啥叫變換。本質上,變換就是函式。 例如,你輸入一個向量 [
04-1 三維空間的線性變換
三維矩陣的幾何意義 經過前兩節二維空間的線性變換的探究,我們可以知道二維矩陣就是為了描述二維空間的線性變換的, 同理,三維矩陣就是描述三維空間的線性變換的 1.變換前的三個基向量是這樣子的 2.變換後的三個基向量的位置,圖上保留了原空間的x,y,z軸
矩陣乘法與斐波那契
矩陣乘法 A*B,只有當A的列數等於B的行數時才有意義,即A為n∗m的矩陣,B為m∗L的矩陣。矩陣的乘法定義如下: [adbecf]∗⎡⎣⎢gikhjl⎤⎦⎥=[ag+bi+ckdg+ei+fkah
奇異值分解(SVD)與線性變換的幾何意義
奇異值分解( The singular value decomposition ) 該部分是從幾何層面上去理解二維的SVD:對於任意的 2 x 2 矩陣,通過SVD可以將一個相互垂直的網格(orthogonal grid)變換到另外一個相互垂直的網格。 我們可以通過向量的方式來描述這個事實
【線性變換/矩陣及乘法】- 圖解線性代數 03
font 公眾 之前 ont 意義 行列式 pan -c nbsp 本文轉自公眾號---遇見數學---圖解數學---線性代數部分 感謝遇見數學工作組將大學課本晦澀難懂、故作高深的數學知識,用通俗易懂而又生動有趣的方法解釋出來。 線性變換是線性空間中的運動, 而矩陣就是用來
【矩陣論】03——線性空間——基座標與座標變換
本系列文章由Titus_1996 原創,轉載請註明出處。 文章連結:https://blog.csdn.net/Titus_1996/article/details/82837074 本系列文章使用的教材為《矩陣論》(第二版),楊明,劉先忠編,華中科技大學出
形象理解線性代數(三)——列空間、零空間(核)、值域、特徵值(特徵向量)、矩陣與空間變換、矩陣的秩
這裡,我們還是要以 形象理解線性代數(一)——什麼是線性變換?為基礎。矩陣對向量的作用,可以理解為線性變換,同時也可以理解為空間的變換,即(m*n)的矩陣會把一個向量從m維空間變換到n維空間。 一、矩陣的列空間與矩陣的秩以及值域的關係 矩陣的列空間,其實就是矩陣的列所組成的空間。比如我們考慮
iOS-矩陣與線性代數的關係____仿射變換
大多數人在高中,或者大學低年級,都上過一門課《線性代數》。這門課其實是教矩陣。 剛學的時候,還蠻簡單的,矩陣加法就是相同位置的數字加一下。 矩陣減法也類似。 矩陣乘以一個常數,就是所有位置都乘以這個數。 但是,等到矩陣乘以矩陣的時候,一切就不一樣了。
【Learning】多項式乘法與快速傅裏葉變換(FFT)
alt 技術 cos 相同 es2017 define ostream 意思 呵呵 簡介: FFT主要運用於快速卷積,其中一個例子就是如何將兩個多項式相乘,或者高精度乘高精度的操作。 顯然暴搞是$O(n^2)$的復雜度,然而FFT可以將其將為$O(n lg
[線性代數] 3.矩陣乘法的幾種求法
com 就是 法則 es2017 img 向量 矩陣 技術分享 組合 已知矩陣A和矩陣B,求A和B的乘積C=AB 矩陣A大小為mxn,矩陣B大小為nxp。 常規方法 矩陣C中每一個元素Cij = A的第i行 乘以(點乘) B的第j列 列方法 矩陣C的第i列 = 矩
02-線性結構2 一元多項式的乘法與加法運算
blog 定義 AC turn HA 例題 pmu 問題 pan 這道題是課上例題,不過課上沒有給出完整代碼,在自己實現時還是遇到了一些細節問題。 1 #include<stdio.h> 2 #include<stdlib.h> 3
02-線性結構2 一元多項式的乘法與加法運算 (java)
02-線性結構2 一元多項式的乘法與加法運算 (20 分) 設計函式分別求兩個一元多項式的乘積與和。 輸入格式: 輸入分2行,每行分別先給出多項式非零項的個數,再以指數遞降方式輸入一個多項式非零項係數和指數(絕對值均為不超過1000的整數)。數字間以空格分隔。
NYOJ298 點的變換 【矩陣乘法經典】
任意門:http://acm.nyist.edu.cn/JudgeOnline/problem.php?pid=298 點的變換 時間限制: 2000 ms | 記憶體限制:65535 KB 難度: 5 &nbs
【矩陣論】07——線性變換——線性變換的矩陣
本系列文章由Titus_1996 原創,轉載請註明出處。 文章連結:https://blog.csdn.net/Titus_1996/article/details/83093450 本系列文章使用的教材為《矩陣論》(第二版),楊明,劉先忠編,華中科技大學出
【矩陣論】06——線性變換——基本概念
本系列文章由Titus_1996 原創,轉載請註明出處。 文章連結:https://blog.csdn.net/Titus_1996/article/details/83088462 本系列文章使用的教材為《矩陣論》(第二版),楊明,劉先忠編,華中科技大學出
【矩陣論】08——線性變換——不變子空間
本系列文章由Titus_1996 原創,轉載請註明出處。 文章連結:https://blog.csdn.net/Titus_1996/article/details/83144567 本系列文章使用的教材為《矩陣論》(第二版),楊明,劉先忠編,華中科技大學出
