匈牙利演算法證明+原理+C++程式碼

阿新 • • 發佈：2018-12-02

介紹

匈牙利演算法用於解決求最大分配的分配問題，不等權重的二分圖中求最大權分配的分配問題，使用KM演算法。

本文首先介紹匈牙利演算法所針對的二分問題

然後介紹匈牙利演算法的原理

最後有匈牙利演算法證明，證明為何使用該演算法可以找到最大匹配

一個典型的分配問題是工作分配，假設有M份工作，總共有N個候選人，假設M小於等於N， $w_{mn}=1$ 表示候選人n勝任工作m，因此我們得到一個關聯矩陣 $S\in \mathbb{R}^{m*n}$ ：

$\begin{bmatrix} 1 & 0 & 1\\ 1 & 1 &1 \\ 0 & 0 & 1 \end{bmatrix}$

對應的圖G為

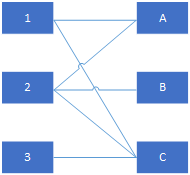
二分圖

二分圖定義

二分圖又稱作二部圖，是圖論中的一種特殊模型。

設G=(V, E)是一個無向圖。如果頂點集V可分割為兩個互不相交的子集X和Y，並且圖中每條邊連線的兩個頂點一個在X中，另一個在Y中，則稱圖G為二分圖。

二分圖性質

定理：當且僅當無向圖G的每一個迴路的次數均是偶數時，G才是一個二分圖。如果無迴路，相當於任一回路的次數為0，故也視為二分圖。

二分圖判斷

如果一個圖是連通的，可以用如下的方法判定是否是二分圖：
在圖中任選一頂點v，定義其距離標號為0，然後把它的鄰接點的距離標號均設為1，接著把所有標號為1的鄰接點均標號為2（如果該點未標號的話），如圖所示，以此類推。
標號過程可以用一次BFS實現。標號後，所有標號為奇數的點歸為X部，標號為偶數的點歸為Y部。
接下來，二分圖的判定就是依次檢查每條邊，看兩個端點是否是一個在X部，一個在Y部。
如果一個圖不連通，則在每個連通塊中作判定。

二分圖匹配

給定一個二分圖G，在G的一個子圖M中，M的邊集{E}中的任意兩條邊都不依附於同一個頂點，則稱M是一個匹配。
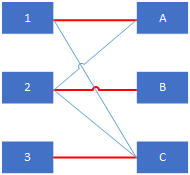
匹配的數量等於E的邊數量。下圖加粗紅色的是一個邊數量為2的匹配。

最大匹配

G的所有子圖中邊數量最大的匹配成為最大匹配。如上圖所示例子，最大邊數為3的子圖只有一種：

完全匹配（完備匹配）

對於數量較少的子集（如上圖L或者R），子集中的每個頂點都和子圖中的某條邊關聯，則稱該子圖所構成的匹配為完全匹配。

完全匹配一定是最大匹配，反過來則不一定。

本質上就是給數量較少的子集所有元素都給匹配了。

研究二分匹配的問題是為了尋找最大匹配，如何尋找？藉助增廣路徑

增廣路徑的定義

增廣路徑的定義：設M為二分圖G已匹配邊的集合，如下圖所示紅色邊

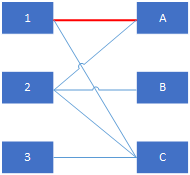
若P是圖G中一條連通兩個未匹配頂點的路徑（P的起點在X部，終點在Y部，反之亦可），並且屬M的邊和不屬M的邊(即已匹配和待匹配的邊)在P上交替出現，則稱P為相對於M的一條增廣路徑。如下圖黃紅色路徑2-A-1-C

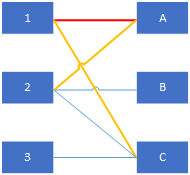
增廣路徑是一條“交錯軌”。

它的第一條邊和最後一條邊都是目前還沒有參與匹配的。因為路徑的起點和終點還沒有被匹配。

這樣交錯進行，顯然P有奇數條邊，因為路徑中不存在迴路，總共有偶數個頂點。並且屬於M的邊數比不屬於M的邊數少1。

匹配增廣

當我們找到一條增廣路徑時，當我們把路徑上屬於M（已經匹配的邊集合）的邊從M中除去，並加入路徑上不屬於M的邊，此時，增廣路徑中已經匹配的頂點依然是匹配狀態，而未匹配的頂點也被匹配了，總的匹配邊數加1。

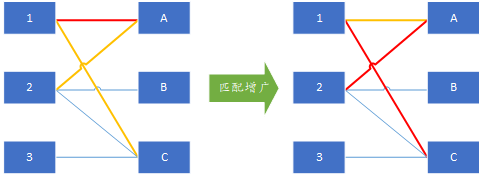
尋找增廣路徑

既然可以通過增廣路徑的匹配增廣操作增加匹配的數量，接下來的問題是在已有的匹配基礎上如何搜尋到一條合適的增廣路徑

如下圖所示紅色線是已有的匹配

那麼我們通過遍歷左邊點集合中未匹配的點，來找所有可用的增廣路徑，頂點1已經匹配了，接下來以未分配的左頂點2為增廣路徑的開始點，在右邊依次遍歷所有可能的頂點，如果找到是一個未分配的頂點如A點，那麼這就是一條增廣鏈2-A，通過增廣操作可以得到如下圖所示分配

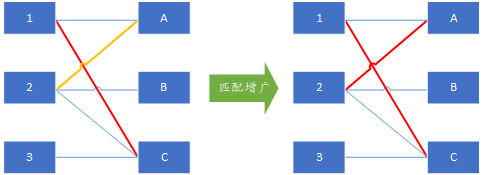
接下來以左邊頂點3為開始點搜尋增廣鏈，3唯一連線的是右邊的C，因此按照增廣鏈的定義，唯一的增廣鏈為3-C-1-A-2-B，通過增廣操作得到最大匹配：

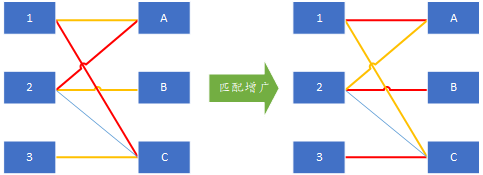
匈牙利演算法的終止條件

當從左邊集合中的某一點開始

沒有搜尋到任何的增廣路徑

這說明該點不是最大匹配必要的點

加入該點後匹配不能增廣

如何證明

命題1、（在當前匹配下）沒有搜尋到增廣鏈就說明該點不是最大匹配的必要點？或者說沒有找到增廣鏈，該匹配就是最大匹配？

命題2、在目前的匹配情況下，沒有搜尋到以該點 $u_{k+1}$ 開始的增廣路徑，在後面加入別的點的匹配情況下，也不可能有以該點開始的增廣路徑存在

這個兩個問題非常重要

參考匈牙利演算法原著……我暫時沒看懂，後面看懂了更新

H.W. Kuhn. The Hungarian method for the assignment problem. Naval Research Logistics Quarterly, 2:83–97, 1955.

定理：存在增廣鏈是增廣當前匹配的充要條件

等價的命題是，為什麼在當前匹配下不存在以左邊某一未匹配點開始的增廣鏈，該點就不是當前匹配下增廣的必要點，即該點不能增廣當前匹配。

從匹配增廣的原理可以看出，以該點開始的增廣鏈是該點可以增廣當前匹配的充分條件

必要條件？

首先能理解的是：如果增廣路徑從左邊開始終止在左邊點

路徑上已經選擇的邊和沒有被選擇的邊數量相同

按照前面介紹進行增廣操作並不能增加比配邊數

然後用反證法去證明如果該點能改善匹配，那麼就一定存在，不需要改變原來匹配點集合的（已經匹配的點一定在改善後的匹配中），以該點開始的增廣鏈

在這裡假設已經匹配的左邊點為 $u_1,u_2,\dots u_k$ ，對應的右邊點為 $v_1,v_2,\dots v_k$

如果該點 $u_{k+1}$ 能改善匹配，那麼根據匹配的獨立性，必然在改善後的匹配中，右邊也有 $k+1$ 個點，而且，只需要一個新的右邊點 $v_{k+1}$ 加入匹配即可（這個可以從下面的分析中可以看出）

1.如果在改善的匹配中， $u_{k+1}$ 匹配的是新點 $v_{k+1}$ ，那麼 $u_{k+1}-v_{k+1}$ 就是一條增廣鏈

2.如果 $u_{k+1}$ 匹配的不是新點 $v_{k+1}$ ，那麼假設 $u_{k+1}$ 匹配的是 $v_{j}$ ， $v_{j}$ 在原來匹配中匹配物件是 $u_{j}$ ，根據匹配唯一性，在改善後的匹配中 $u_{j}$ 匹配的肯定不是 $v_{j}$ ，如果 $u_{j}$ 匹配的是新點 $v_{k+1}$ ，那麼 $u_{k+1}-v_{j}-u{j}-v_{k+1}$ 就是一條增廣鏈

3.如果 $u_{j}$ 匹配的還是原來匹配的點，那就繼續上面的分析2，根據已經匹配點數量是有限的，當分析到最後一個左邊點時，根據匹配的唯一性，它必然和新點 $v_{k+1}$ 連線（因為舊點只有k個），那麼增廣鏈依然存在（ $u_{k+1}$ 開始， $v_{k+1}$ 結束，中間穿過所有的 $u_1,u_2,\dots u_k$ 和 $v_1,v_2,\dots v_k$ ）

綜上分析，如果存在改善匹配包含了該新點，那麼就必然存在一條以該點開始的增廣鏈，而且新增的右邊點僅僅有一個，不需要另外的點去替換原來的右邊點

引理：那麼根據存在增廣鏈是增廣當前匹配的充要條件，演算法只要遍歷所有未匹配的左邊點，沒有找到增廣鏈，即可終止演算法，找到最大匹配

另外一方面

定理：在目前的匹配情況下

沒有搜尋到以該點 $u_{k+1}$ 開始的增廣路徑

在後面加入別的點的匹配情況下，也不可能有以該點開始的增廣路徑存在

（這個保證了演算法只要遍歷一遍左邊點即可，不需要重複遍歷）

證明：

原來的匹配 $M$ 為 $u_1,u_2,\dots u_k$ ，對應的右邊點為 $v_1,v_2,\dots v_k$

如果加入新點 $u'$ 和 $v'$ 時，所使用的增廣鏈為 ${\color{Purple} u'-v_{j_1}-u_{j_1}-\cdots-v_{j_m}-u_{j_m}-v'}$ ，改善後的匹配 $M'$ 變成 $u_1,u_2,\dots u_p$ 和對應的 $v_1,v_2,\dots v_p$ ，p=k+1

前提： $u_{k+1}$ 在原來的匹配下沒有增廣路徑

假設 $u_{k+1}$ 在改善後的匹配下存在增廣路徑

1、如果增廣路徑 ${\color{Red} u_{k+1}-v_{l_1}-u_{l_1}-\cdots-v_{l_n}-u_{l_n}-v_{k+1}}$ 中不存在， ${\color{Purple} u'-v_{j_1}-u_{j_1}-\cdots-v_{j_m}-u_{j_m}-v'}$ 中的 $v$ ，那麼增廣路徑肯定不存在 $u'$ ，因為改善匹配中存在匹配 $u'-v_{j1}$ ，所以

${\color{Red} u_{k+1}-v_{l_1}-u_{l_1}-\cdots-v_{l_n}-u_{l_n}-v_{k+1}}$ 中的 $u_l$ 和 $v_l$ 都是原匹配 $M$ 中的，因此這是原匹配中的一條增廣路徑，和前提相悖

2、如果增廣路徑 ${\color{Red} u_{k+1}-v_{l_1}-u_{l_1}-\cdots-v_{l_n}-u_{l_n}-v_{k+1}}$ 中存在， ${\color{Purple} u'-v_{j_1}-u_{j_1}-\cdots-v_{j_m}-u_{j_m}-v'}$ 中的 $v$ ，那麼原匹配中必然存在增廣路徑 ${\color{Red} u_{k+1}-v_{l_1}-u_{l_1}-\cdots-v_{l_p}-u_{l_p}}-{\color{Purple}v_{j_q}-u_{j_q}-\cdots-v_{j_m}-u_{j_m}-v' }$ ，也是原匹配中的一條增廣路徑，和前提相悖

綜上即證

上面的兩條命題成立

當增廣路徑搜尋演算法，遍歷一遍左邊頂點集合後

已經加入最大匹配的點已經加入

沒有加入的，也不可能通過加入該點增廣匹配了

匹配已經達到最大，演算法終止

C++演算法程式碼

#include<iostream>
#include<cstring>
using namespace std;
const int maxn = 3;
int n = maxn, m = maxn;
int Map[maxn][maxn];//map[i][j]=1表示X部的i和Y部的j存在路徑,是否可以匹配
int cx[maxn], cy[maxn];
bool vis[maxn];
//cx[i]表示X部i點匹配的Y部頂點的編號
//cy[i]表示Y部i點匹配的X部頂點的編號

bool dfs(int u)//dfs進入的都是X部的點
{
	for (int v = 0; v < n; v++)//列舉Y部的點，判斷X部的u和Y部的v是否存在路徑
	{
		//如果存在路徑並且還沒被標記加入增廣路
		if (Map[u][v] && !vis[v])//vis陣列只標記Y組
		{
			//標記加入增廣路
			vis[v] = 1;

			//如果Y部的點v還未被匹配
			//或者已經被匹配了，但是可以從v點原來匹配的cy[v]找到一條增廣路
			//說明這條路就可是一個正確的匹配
			//因為遞迴第一次進入dfs時，u是未匹配的
			//如果v還沒有匹配物件，即和它相連的所有邊都不在，已經選擇的匹配邊集合M（M\in E）中，這時就找到了u-v增廣路徑
			//如果v已經有匹配物件了，那麼u-v是一條未選擇的邊，而v-cy[v] \in M 則是一條已經選擇的邊, dfs(cy[v])從cy[v]開始搜尋增廣路徑
				//如果新的v'沒有匹配物件，那麼u-v-cy[v]-v'就是一條增廣路徑，如果v'已經有匹配物件了，那麼根據匹配是唯一的，cy[v]-v'一定不在已經選擇的邊中(和cy[v]-v衝突)，u-v-cy[v]-v'-cy[v']符合增廣路徑對邊順序的要求，繼續利用dfs(cy[v'])搜尋u-v-cy[v]-v'-cy[v']-下面的點
				//當搜尋到增廣鏈時，如u-v-cy[v]-v',那麼經過遞迴的匹配調整和return 1，進行匹配增廣操作，假設dfs0 是main呼叫的dfs演算法，dfs1是dfs0呼叫的dfs演算法
				//在dfs1中進行cy[v]-v'的匹配，因為dfs1返回1，因此在dfs0中進行u-v的匹配，匹配增廣操作的結果是{cy[v]-v}->{u-v,cy[v]-v'}
				//如果在一個dfs(k)自呼叫的dfs(k+1)中，遍歷所有的v(k+1),要麼已經有匹配點了，要麼和輸入u(k+1)沒有連線可能，這時搜尋終止，說明不存在經過u(k+1)的增廣鏈，返回0
				//而在main呼叫的dfs(0)中，呼叫的dfs(1)返回的都是0，而且v都是已經有匹配了，那麼不存在從該點出發的增廣鏈，那麼就該點就不在最大匹配當中
				//為什麼找不到增廣鏈就不在最大匹配當中呢？感覺可以用反證法證明，部落格中下面內容可能有更新這方面的思考
			if (cy[v] == -1 || dfs(cy[v]))
			{
				cx[u] = v;//可以匹配，進行匹配
				cy[v] = u;
				return 1;
			}
		}
	}
	return 0;//不能匹配
}
int maxmatch()//匈牙利演算法主函式
{
	int ans = 0;
	//匹配清空，全部置為-1
	memset(cx, -1, sizeof(cx));
	memset(cy, -1, sizeof(cy));
	for (int i = 0; i < n; i++)
	{
		if (cx[i] == -1)//如果X部的i還未匹配
		{
			memset(vis, 0, sizeof(vis));//每次找增廣路的時候清空vis
			ans += dfs(i);
		}
	}
	return ans;
}

int main_test()
{
	//輸入匹配的兩個點集合的數量
	cin >> n >> m;
	//輸入兩個點集合成員間的匹配可能
	int x, y;
	for (int i = 0; i < m; i++)
	{
		cin >> x >> y;
		Map[x][y] = 1;
	}
	//執行匈牙利演算法，輸出最大匹配
	cout << maxmatch() << endl;
}

匈牙利演算法證明+原理+C++程式碼

介紹