【演算法】牛客網演算法進階班(經典題目選講(1))
經典題目選講(1)
題目一:The Skyline Problem
給定一個Ñ行3列的二維陣列,每一行表示有一座大樓,一共有Ñ座大樓所有大樓的底部都坐落在X軸上,每一行的三個值(A,B, C)代表每座大樓的從(A,0)點開始,到(B,0)點結束,高度為C。輸入的資料可以保證A<B,且A,B,C均為正數。大樓之間可以有重合。請輸出整體的輪廓線。

例如:給定一個二維陣列[[1,3,3],[2,4,4],[5,6,1]
輸出為輪廓線[[1,2,3],[2,4,4],[5,6,1]
思考:本題使用有序表結構,但關鍵在於設計處理流程。以[2,5,6]為例,將其變為(2,+6)和(5,-6)分別表示,在2的位置上,高度增加了6,在5的位置上,高度減了6.
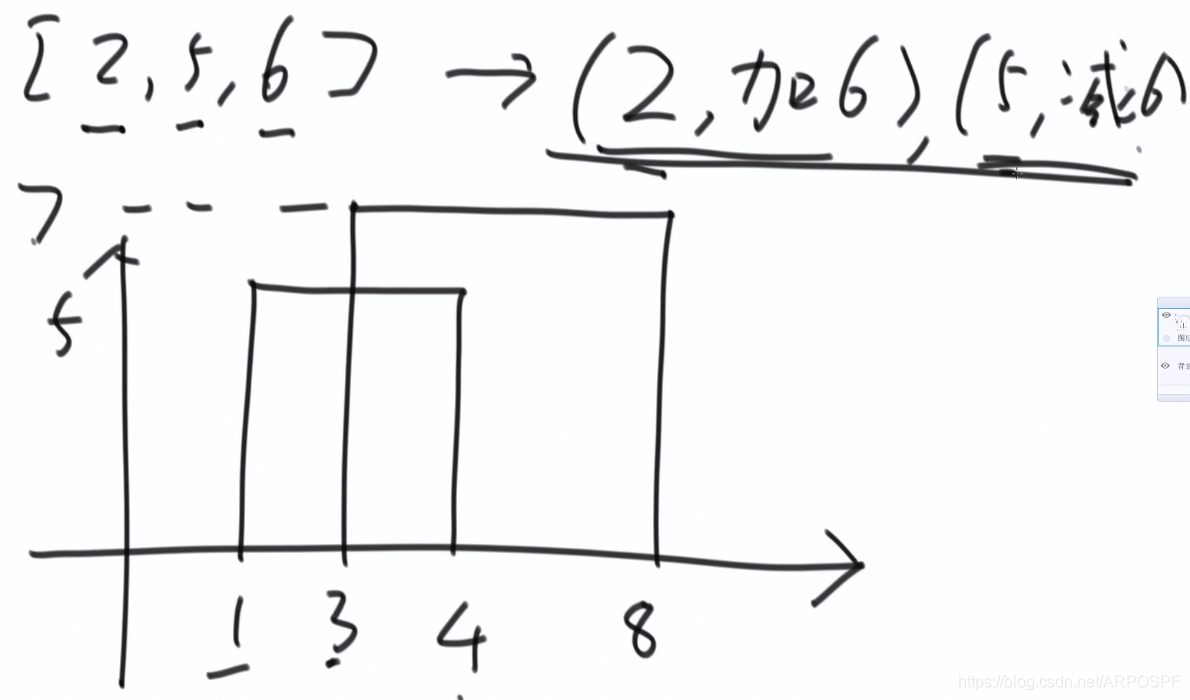
將這樣的操作之後的陣列排序:第一維(第一個數)從小到大,第一維相等的時候,第二維按照+的放在前面,-的放在後面,但是對於同樣是+或-的兩個值,誰放前面都可以。例如(6,-5),(6,-7),誰在前面都可以,但是(12,+4)必須放在(12,-5)之前。
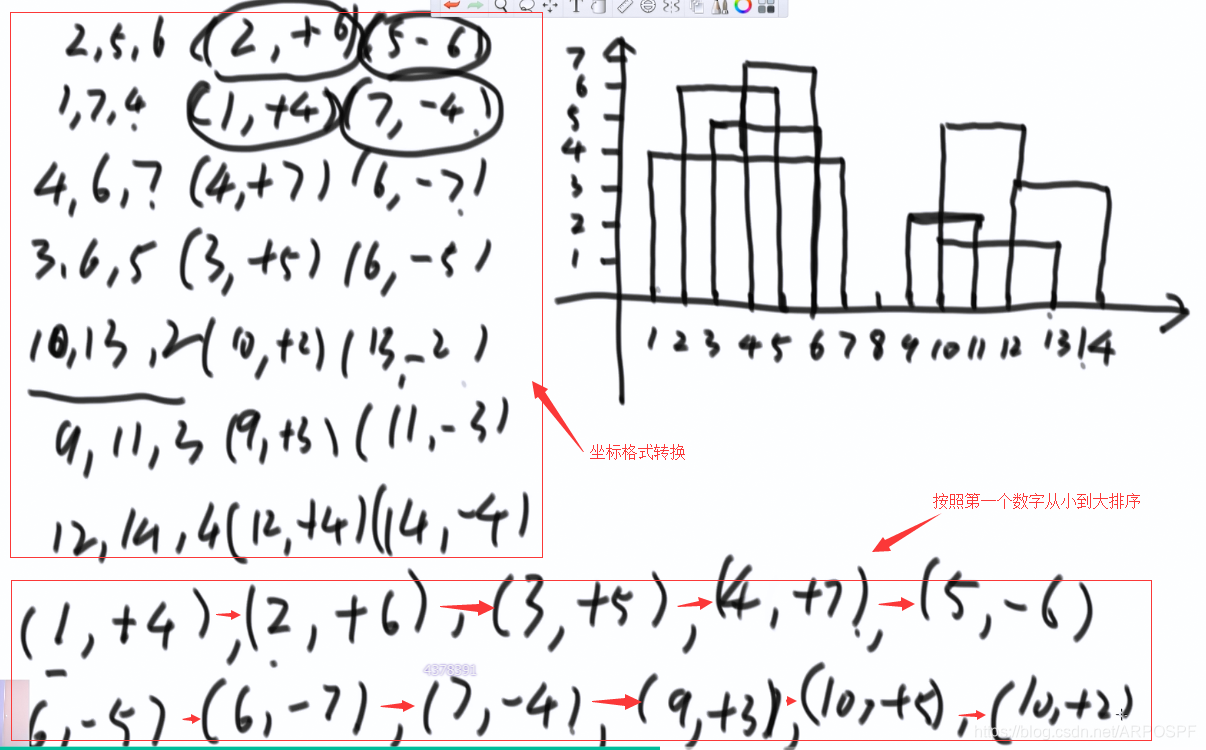
輪廓線的產生:最大高度發生了變化。定義有序表map,key是高度,value是次數。依次遍歷陣列,在此過程中根據最大高度的變化判定輪廓線的變化和高度。當次數減少到0的時候,刪除該條記錄。程式碼如下:
import java.util.*; public class BuildingOutline { /** * 操作物件的類 */ public static class Node { public boolean isAdd; //true;false public int x; public int h; public Node(boolean isAddHeight, int position, int height) { isAdd = isAddHeight; x = position; h = height; } } //比較器 public static class NodeComparator implements Comparator<Node> { @Override public int compare(Node o1, Node o2) { if (o1.x != o2.x) { return o1.x - o2.x; } if (o1.isAdd != o2.isAdd) { return o1.isAdd ? -1 : 1; } return 0; } } /** * @param buildings n行3列的矩陣 * @return */ public static List<List<Integer>> buildingOutline(int[][] buildings) { Node[] nodes = new Node[buildings.length * 2];//運算元組 for (int i = 0; i < buildings.length; i++) { nodes[i * 2] = new Node(true, buildings[i][0], buildings[i][2]); nodes[i * 2 + 1] = new Node(false, buildings[i][1], buildings[i][2]); } Arrays.sort(nodes, new NodeComparator()); TreeMap<Integer, Integer> heightTimesMap = new TreeMap<>(); //某一個高度出現的次數 TreeMap<Integer, Integer> xMaxHeightMap = new TreeMap<>(); for (int i = 0; i < nodes.length; i++) { if (nodes[i].isAdd) {//加高度的操作 if (!heightTimesMap.containsKey(nodes[i].h)) {//如果不含有此高度,則次數為1,否則次數加1 heightTimesMap.put(nodes[i].h, 1); } else { heightTimesMap.put(nodes[i].h, heightTimesMap.get(nodes[i].h) + 1); } } else {//減高度的操作 if (heightTimesMap.get(nodes[i].h) == 1) { //如果減完之後次數為0,則直接刪除這條記錄 heightTimesMap.remove(nodes[i].h); } else { heightTimesMap.put(nodes[i].h, heightTimesMap.get(nodes[i].h) - 1); } } //跟蹤記錄最大高度的變化 if (heightTimesMap.isEmpty()) { xMaxHeightMap.put(nodes[i].x, 0); } else { xMaxHeightMap.put(nodes[i].x, heightTimesMap.lastKey()); } } //生成最後的輪廓線 List<List<Integer>> res = new ArrayList<>(); int start = 0; int height = 0; for (Map.Entry<Integer, Integer> entry : xMaxHeightMap.entrySet()) { int curPosition = entry.getKey(); int curMaxHeight = entry.getValue(); if (height != curMaxHeight) { if (height != 0) { List<Integer> newRecord = new ArrayList<>(); newRecord.add(start); newRecord.add(curPosition); newRecord.add(height); res.add(newRecord); } start = curPosition; height = curMaxHeight; } } return res; } }
題目二:設計可以變更的快取結構(LRU)
題目描述:設計一種快取結構,該結構在構造時確定大小,假設大小為K,並由兩個功能:
- 集(鍵,值):將記錄(鍵,值)插入該結構
- 獲得(鍵):返回鍵對應的值值
要求:
- 設定和獲取方法的時間複雜度為O(1)。
- 某個鍵的設定或GET操作一旦發生,認為這個關鍵的記錄成了最經常使用的。
- 當快取的大小超過ķ時,移除最不經常使用的記錄,即設定或獲取最久遠的。
舉例:
假設快取結構的例項是快取記憶體,大小為3,並依次發生如下行為:
- cache.set( “A”,1)。最經常使用的記錄為(“A”,1)。
- cache.set( “B”,2)。最經常使用的記錄為(“B”,2),(“A”,1)變為最不經常的。
- cache.set( “C”,3)。最經常使用的記錄為(“C”,2),(“A”,1)還是最不經常的。
- cache.get( “A”)。最經常使用的記錄為(“A”,1),( “B”,2)變為最不經常的。
- cache.set( “d”,4)。大小超過了3,所以移除此時最不經常使用的記錄(“B”,2),加入記錄(“d”,4),並且為最經常使用的記錄,然後(“C”,2)變為最不經常使用的記錄。
思考:這種快取結構可以由雙端佇列與雜湊表相結合的方式實現。首先實現一個基本的雙向連結串列節點的結構:
public class Node<V>{
public V value;
public Node<V> last;
public Node<V> next;
public Node(V value){
this.value=value;
}
}根據雙向連結串列節點結構Node,實現一種雙向連結串列結構NodeDoubleLinkedList,在該結構中優先順序最低的節點是head(頭),優先順序最高的節點是tail(尾)。這個結構有以下三種操作:
- 當加入一個節點時,將新加入的節點放在這個連結串列的尾部,並將這個節點設定為新的尾部,參見如下程式碼中的addNode方法。
- 對這個結構中的任意節點,都可以分離出來並放到整個連結串列的尾部,參見如下程式碼中的moveNodeToTail方法
- 移除head節點並返回這個節點,然後將head設定成老head節點的下一個,參見如下程式碼中的removeHead方法。
public class NodeDoubleLinkedList<V> {
private Node<V> head;
private Node<V> tail;
public NodeDoubleLinkedList() {
this.head = null;
this.tail = null;
}
public void addNode(Node<V> newNode) {
if (newNode == null) {
return;
}
if (this.head == null) {
this.head = newNode;
this.tail = newNode;
} else {
this.tail.next = newNode;
newNode.last = this.tail;
this.tail = newNode;
}
}
public void moveNodeToTail(Node<V> node) {
if (this.tail == node) {
return;
}
if (this.head == node) {
this.head = node.next;
this.head.last = null;
} else {
node.last.next = node.next;
node.next.last = node.last;
}
node.last = this.tail;
node.next = null;
this.tail.next = node;
this.tail = node;
}
public Node<V> removeHead() {
if (this.head == null) {
return null;
}
Node<V> res = this.head;
if (this.head == this.tail) {
this.head = null;
this.tail = null;
} else {
this.head = res.next;
res.next = null;
this.head.last = null;
}
return res;
}
}最後實現最終的快取結構。如何把記錄之間按照“訪問經常度”來排序,就是上下文提到的NodeDoubleLinkedList結構。一旦接入新的記錄,就把該記錄加到NodeDoubleLinkedList的尾部(addNode)。一旦獲得(get)或設定(set)一個記錄的key,就將這個key對應的node在NodeDoubleLinkedList中調整到尾部(moveNodeToTail)。一旦cache滿了,就刪除“最不經常使用”的記錄,也就是移除NodeDoubleLinkedList的當前頭部(removeHead)。
為了能讓每一個key都能找到在NodeDoubleLinkedList所對應的節點,同時讓每一個node都能找到各自的key,我們還需要兩個map分別記錄key到node的對映,以及node到key的對映,就是如下MyCache結構中的keyNodeMap和nodeKeyMap。
public class MyCache<K, V> {
private HashMap<K, Node<V>> keyNodeMap;
private HashMap<Node<V>, K> nodeKeyMap;
private NodeDoubleLinkedList<V> nodeList;
private int capacity;
public MyCache(int capacity) {
if (capacity < 1) {
throw new RuntimeException("Shoule be more than 0.");
}
this.keyNodeMap = new HashMap<>();
this.nodeKeyMap = new HashMap<>();
this.nodeList = new NodeDoubleLinkedList<>();
this.capacity = capacity;
}
public V get(K key) {
if (this.keyNodeMap.containsKey(key)) {
Node<V> res = this.keyNodeMap.get(key);
this.nodeList.moveNodeToTail(res);
return res.value;
}
return null;
}
public void set(K key, V value) {
if (this.keyNodeMap.containsKey(key)) {
Node<V> node = this.keyNodeMap.get(key);
node.value = value;
this.nodeList.moveNodeToTail(node);
} else {
Node<V> newNode = new Node<V>(value);
this.keyNodeMap.put(key, newNode);
this.nodeKeyMap.put(newNode, key);
this.nodeList.addNode(newNode);
if (this.keyNodeMap.size() == this.capacity + 1) {
this.removeMostUnusedCache();
}
}
}
private void removeMostUnusedCache() {
Node<V> removeNode = this.nodeList.removeHead();
K removeKey = this.nodeKeyMap.get(removeNode);
this.nodeKeyMap.remove(removeNode);
this.keyNodeMap.remove(removeKey);
}
}完整程式碼如下:
package NowCoder2.Class04;
import java.util.HashMap;
public class LRU {
public static class Node<K, V> { //雙向連結串列結構
public K key;
public V value;
public Node<K, V> last;
public Node<K, V> next;
public Node(K key, V value) {
this.key = key;
this.value = value;
}
}
public static class NodeDoubleLinkedList<K, V> {
private Node<K, V> head;
private Node<K, V> tail;
public NodeDoubleLinkedList() {
this.head = null;
this.tail = null;
}
public void addNode(Node<K, V> newNode) {
if (newNode == null) {
return;
}
if (this.head == null) {
this.head = newNode;
this.tail = newNode;
} else {
this.tail.next = newNode;
newNode.last = this.tail;
this.tail = newNode;
}
}
//node已經在連結串列上
public void moveNodeToTail(Node<K, V> node) {
if (this.tail == node) {
return;
}
//node不是尾節點
if (this.head == node) {
this.head = node.next;
this.head.last = null;
} else {
node.last.next = node.next;
node.next.last = node.last;
}
node.last = this.tail;
node.next = null;
this.tail.next = node;
this.tail = node;
}
//頭節點remove並且返回
public Node<K, V> removeHead() {
if (this.head == null) {
return null;
}
Node<K, V> res = this.head;
if (this.head == this.tail) {//雙向連結串列中只有一個節點的時候
this.head = null;
this.tail = null;
} else {//不止一個的時候
this.head = res.next;
res.next = null;
this.head.last = null;
}
return res;
}
}
public static class MyCache<K, V> {
private HashMap<K, Node<K, V>> keyNodeMap;
private NodeDoubleLinkedList<K, V> nodeList;
private int capacity; //快取的容量,固定大小
public MyCache(int capacity) {
if (capacity < 1) {
throw new RuntimeException("should be more than 0");
}
this.keyNodeMap = new HashMap<>();
this.nodeList = new NodeDoubleLinkedList<>();
this.capacity = capacity;
}
public V get(K key) {
if (this.keyNodeMap.containsKey(key)) {
Node<K, V> res = this.keyNodeMap.get(key);
this.nodeList.moveNodeToTail(res);
return res.value;
}
return null;
}
public void set(K key, V value) {
if (this.keyNodeMap.containsKey(key)) {
Node<K, V> node = this.keyNodeMap.get(key);
node.value = value;
this.nodeList.moveNodeToTail(node);
} else {//新建操作
Node<K, V> newNode = new Node<>(key, value);
this.keyNodeMap.put(key, newNode);
this.nodeList.addNode(newNode);
if (this.keyNodeMap.size() == this.capacity + 1) {
removeUnusedCache();
}
}
}
private void removeUnusedCache() {
this.keyNodeMap.remove(this.nodeList.removeHead().key);
}
}
public static void main(String[] args) {
MyCache<String, Integer> testCache = new MyCache<>(3);
testCache.set("A", 1);
testCache.set("B", 2);
testCache.set("C", 3);
System.out.println(testCache.get("B"));
System.out.println(testCache.get("A"));
testCache.set("D", 4);
System.out.println(testCache.get("D"));
System.out.println(testCache.get("C"));
}
}
題目三:實現LFU快取結構
上一題實現了LRU快取演算法,LFU也是一個著名的快取演算法,自行了解之後實現LFU中的設定和GET。
要求:兩個方法的時間複雜度都為O(1)。
LFU:在快取中使用次數最小的被移除,如果次數都一樣多,誰最早進快取,刪除誰。
思路:桶結構,桶表示次數,桶內部節點之間通過雙向連結串列連線,桶與桶之間也通過雙向連結串列連線。兩張表和一個二維雙向連結串列實現該資料結構。
程式碼:
package NowCoder2.Class04;
import java.util.HashMap;
public class LFU {
public static class Node {
public Integer key;
public Integer value;
public Integer times;
public Node up;
public Node dowm;
public Node(int key, int value, int times) {
this.key = key;
this.value = value;
this.times = times;
}
}
public static class NodeBucket {
public Node head;
public Node tail;
public NodeBucket last;
public NodeBucket next;
public NodeBucket(Node node) {
head = node;
tail = node;
}
public void addNodeFromHead(Node newHead) {
newHead.dowm = head;
head.up = newHead;
head = newHead;
}
public boolean isEmpty() {
return head == null;
}
//潛臺詞:node 已經確定在桶中
public void deleteNode(Node node) {
if (head == tail) {//只剩一個節點
head = null;
tail = null;
} else {//不止一個節點
if (node == head) {
head = node.dowm;
head.up = null;
} else if (node == tail) {
tail = node.up;
tail.dowm = null;
} else {
node.up.dowm = node.dowm;
node.dowm.up = node.up;
}
}
node.up = null;
node.dowm = null;
}
}
public static class LFUCache {
private int capacity;//總記憶體限制
private int size;//目前收了多少資料
private HashMap<Integer, Node> keyNodeMap;
private HashMap<Node, NodeBucket> nodeBucketMap;
private NodeBucket headBucket;
public LFUCache(int capacity) {
this.capacity = capacity;
this.size = 0;
this.keyNodeMap = new HashMap<>();
this.nodeBucketMap = new HashMap<>();
headBucket = null;
}
public void set(int key, int value) {
if (keyNodeMap.containsKey(key)) {//更新
Node node = keyNodeMap.get(key);
node.value = value;
node.times++;
NodeBucket curNodeBucket = nodeBucketMap.get(node);
move(node, curNodeBucket);//node從老桶出,進次數+1的桶,有,直接進,無,新建
} else {//新建記錄
if (size == capacity) {
Node deleteNode = headBucket.tail;
headBucket.deleteNode(deleteNode);
deleteBucketModifyHeadBucket(headBucket);
keyNodeMap.remove(deleteNode.key);
nodeBucketMap.remove(deleteNode);
size--;
}
//記憶體夠用
Node node = new Node(key, value, 1);
if (headBucket == null) {
headBucket = new NodeBucket(node);
} else {
if (headBucket.head.times.equals(node.times)) {
headBucket.addNodeFromHead(node);
} else {//頭桶詞頻不是1
NodeBucket newBucket = new NodeBucket(node);
newBucket.next = headBucket;
headBucket.last = newBucket;
headBucket = newBucket;
}
}
keyNodeMap.put(key, node);
nodeBucketMap.put(node, headBucket);
size++;
}
}
//已經確定node屬於oldBucket
//但此時該node運算元量增加,所以需要從老的桶中,刪掉
//加入到運算元量+1的新桶中
//如果運算元量+1的下一個桶已經存在,直接放
//否則,新建運算元量+1的下一個桶
//老桶可以會刪除,刪除的時候也可能存在換頭桶的情況
//並且保持桶之間,依然是雙向連結串列連線
private void move(Node node, NodeBucket oldBucket) {
oldBucket.deleteNode(node);
//node要放入新桶中,對於新桶來說,前一個是誰
NodeBucket preBucket = deleteBucketModifyHeadBucket(oldBucket) ? oldBucket.last :oldBucket;
NodeBucket nextBucket = oldBucket.next;
//新桶目前還沒有建立出來
if (nextBucket == null) {//node之前就是最大詞頻,需要更大詞頻的桶
NodeBucket newBucket = new NodeBucket(node);
if (preBucket != null) {
preBucket.next = nextBucket;
}
newBucket.last = preBucket;
if (headBucket == null) {//第一個桶剛剛被建立的情況
headBucket = newBucket;
}
nodeBucketMap.put(node, newBucket);
} else {//node原來的桶,存在下一個桶
if (nextBucket.head.times.equals(node.times)) {
nextBucket.addNodeFromHead(node);
nodeBucketMap.put(node, nextBucket);
} else {//老桶下一個桶的詞頻,比node詞頻++之後大
NodeBucket newBucket = new NodeBucket(node);
if (preBucket != null) {
preBucket.next = nextBucket;
}
newBucket.last = preBucket;
newBucket.next = nextBucket;
newBucket.last = newBucket;
if (headBucket == nextBucket) {
headBucket = newBucket;
}
nodeBucketMap.put(node, newBucket);
}
}
}
//如果當前的桶是空的,刪掉他
//如果刪掉的桶又是頭桶的話,換頭桶
//如果真的刪了,返回true
//如果不需要刪,返回false
private boolean deleteBucketModifyHeadBucket(NodeBucket bucket) {
if (bucket.isEmpty()) {
if (headBucket == bucket) {
headBucket = bucket.next;
if (headBucket != null) {
headBucket.last = null;
}
} else {
bucket.last.next = bucket.next;
if (bucket.next != null) {
bucket.next.last = bucket.last;
}
}
return true;
}
return false;
}
public int get(int key) {
if (!keyNodeMap.containsKey(key)) {
return -1;
}
Node node = keyNodeMap.get(key);
node.times++;
NodeBucket curNodeList = nodeBucketMap.get(node);
move(node, curNodeList);
return node.value;
}
}
}
題目四:找到二叉樹中的最大搜索二叉子樹
題目描述:給定一棵二叉樹的頭節點head,已知其中所有節點的值都不一樣,找到含有節點最多的搜尋二叉子樹,並返回這棵子樹的頭節點。
要求:如果節點數為N,要求時間複雜度為O(N),額外空間複雜度為O(h),h為二叉樹的高度。
思路:
以節點node為頭的樹中,最大的搜尋二叉子樹只可能來自以下兩種情況:
第一種:如果來自node左子樹上的最大搜索二叉子樹是以node.left為頭的;來自node右子樹上的最大搜索二叉子樹是以node.right為頭的;node左子樹上的最大搜索二叉子樹的最大值小於node.value;node右子樹上的最大搜索二叉子樹的最小值大於node.value,那麼以節點node為頭的整課樹都是搜尋二叉樹。
第二種:如果不滿足第一種情況,說明以節點node為頭的數整體不能連成搜尋二叉樹,這種情況下,以node為頭的樹上的最大搜索二叉子樹是來自node的左子樹上的最大搜索二叉子樹和來自node的右子樹上的最大搜索二叉子樹之間,節點數較多的那個。
通過以上的分析,求解的具體過程如下:
- 整體過程是二叉樹的後序遍歷
- 遍歷到當前節點記為cur時,先遍歷cur的左子樹收集4個資訊,分別是左子樹上的最大搜索二叉子樹的頭節點(lBST)、節點數(lSize)、最小值(lMin)和最大值(lMax)。在遍歷cur的右子樹收集4個資訊,分別是右子樹上最大搜索二叉子樹的頭節點(rBST)、節點數(rSize)、最小值(rMin)和最大值(rMax)。
- 根據步驟2所收集的資訊,判斷是否滿足第一種情況,如果滿足第一種情況,就返回cur節點,如果滿足第二種情況,就返回lBST和rBST中較大的一個。
- 可以使用全域性變數的方式實現步驟2中收集節點數、最小值和最大值的問題。
程式碼:
package NowCoder2.Class04;
public class BiggestSubBST {
public class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
public Node biggestSubBST(Node head) {
int[] record = new int[3];
return posOrder(head, record);
}
private Node posOrder(Node head, int[] record) {
if (head == null) {
record[0] = 0;
record[1] = Integer.MAX_VALUE;
record[2] = Integer.MIN_VALUE;
return null;
}
int value = head.value;
Node left = head.left;
Node right = head.right;
Node lBST = posOrder(left, record);
int lSize = record[0];
int lMin = record[1];
int lMax = record[2];
Node rBST = posOrder(right, record);
int rSize = record[0];
int rMin = record[1];
int rMax = record[2];
record[1] = Math.min(lMin, value);
record[2] = Math.max(rMax, value);
if (left == lBST && right == rBST && lMax < value && value < rMin) {
record[0] = lSize + rSize + 1;
return head;
}
record[0] = Math.max(lSize, rSize);
return lSize > rSize ? lBST : rBST;
}
}
題目五:給定一棵二叉樹的頭節點的頭,請返回最大搜索二叉子樹的大小
題目描述:給定一棵二叉樹的頭節點head,已知所有節點的值都不一樣,返回其中最大的且符合搜尋二叉樹條件的最大拓撲結構的大小。
思考:
方法一:二叉樹的節點數為N,時間複雜度為O(N^2)的方法。
首先來看這樣一個問題,以節點head為頭的樹中,在拓撲結構中也必須以head為頭的情況下,怎麼找到符合搜尋二叉樹條件的最大結構?這個問題有一種比較容易理解的解法,先考察head的孩子節點,根據孩子節點的值從head開始按照二叉搜尋的方式移動,如果最後能移動到同一個孩子節點上,說明這個孩子節點可以作為這個拓撲的一部分,並繼續考查這個孩子節點的孩子節點,一直延伸下去。
也就是說,我們根據一個節點的值,根據這個值的大小,共head開始,每次向左或向右移動,如果最後能移動到原來的節點上,說明該節點可以作為以head為頭的拓撲的一部分。
解決了以節點head為頭的樹中,在拓撲結構也必須以head為頭的情況下,怎麼找到符合搜尋二叉樹條件的最大結構?接下來只需要遍歷所有的二叉樹節點,並在以每個節點為頭的子樹中都求一遍其中的最大拓撲結構,其中最大的那個就是我們想找的結構,它的大小就是返回值。
方法二:二叉樹的節點數為N、時間複雜度最好為O(N)、最差為O(NlogN)的方法。
首先介紹一個非常重要的概念——拓撲貢獻記錄。每個節點的旁邊都有被括號括起來的兩個值,把它稱為節點對當前頭節點的拓撲貢獻記錄。第一個值代表節點的左子樹可以為當前頭節點的拓撲貢獻幾個節點,第二個值代表節點的右子樹可以為當前頭節點的拓撲貢獻幾個節點。整個方法二的核心就是如果分別得到了head左右兩個孩子為頭的拓撲貢獻記錄,可以快速得到以head為頭的拓撲貢獻記錄。
當我們得到以head為頭的拓撲貢獻記錄後,相當於求出了以head為頭的最大拓撲的大小。方法二正是不斷地用這種方法,從小樹的記錄整合成大樹的記錄,從而求出整棵樹中符合搜尋二叉樹條件的最大拓撲的大小。所以整個過程大體說來是利用二叉樹的後序遍歷,對每個節點來說,先生成其左孩子的記錄,然後是右孩子的記錄,接著把兩組記錄修改成以這個節點為頭的拓撲貢獻記錄,並找出所有節點的最大拓撲大小中最大的那個。
方法一和方法二的程式碼如下:
package NowCoder2.Class04;
import java.util.HashMap;
import java.util.Map;
public class BSTTopoSize {
// ****** 方法一 ******
public class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
public int bstTopoSize1(Node head) {
if (head == null) {
return 0;
}
int max = maxTopo(head, head);
max = Math.max(bstTopoSize1(head.left), max);
max = Math.max(bstTopoSize1(head.right), max);
return max;
}
public int maxTopo(Node h, Node n) {
if (h != null && n != null && isBSTNode(h, n, n.value)) {
return maxTopo(h, n.left) + maxTopo(h, n.right) + 1;
}
return 0;
}
public boolean isBSTNode(Node h, Node n, int value) {
if (h == null) {
return false;
}
if (h == n) {
return true;
}
return isBSTNode(h.value > value ? h.left : h.right, n, value);
}
// ****** 方法一結束 *******
// ****** 方法二 ********
public class Record {
public int l;
public int r;
public Record(int left, int right) {
this.l = left;
this.r = right;
}
}
public int bstTopoSize2(Node head) {
Map<Node, Record> map = new HashMap<>();
return posOrder(head, map);
}
public int posOrder(Node h, Map<Node, Record> map) {
if (h == null) {
return 0;
}
int ls = posOrder(h.left, map);
int rs = posOrder(h.right, map);
modifyMap(h.left, h.value, map, true);
modifyMap(h.right, h.value, map, false);
Record lr = map.get(h.left);
Record rr = map.get(h.right);
int lbst = lr == null ? 0 : lr.l + lr.r + 1;
int rbst = rr == null ? 0 : rr.l + rr.r + 1;
map.put(h, new Record(lbst, rbst));
return Math.max(lbst + rbst + 1, Math.max(ls, rs));
}
public int modifyMap(Node n, int v, Map<Node, Record> m, boolean s) {
if (n == null || (!m.containsKey(n))) {
return 0;
}
Record r = m.get(n);
if ((s & n.value > v) || ((!s) && n.value < v)) {
m.remove(n);
return r.l + r.r + 1;
} else {
int minus = modifyMap(s ? n.right : n.left, v, m, s);
if (s) {
r.r = r.r - minus;
} else {
r.l = r.l - minus;
}
m.put(n, r);
return minus;
}
}
// ****** 方法二結束 *******
}
題目六:未排序陣列中累加和為給定值的最長子陣列系列問題
題目描述:給定一個無序陣列arr,其中元素可正、可負、可0,給定一個整數k,求arr所有的子陣列中累加和等於k的最長子陣列的長度
示例:arr = {7,3,2,1,1,7,7,7} num = 7
其中有很多的子陣列累加和等於7,但是最長的子陣列是{3,2,1,1},所以返回其長度4。
補充題目1:給定一個無序陣列arr,其中元素可正、可負、可0。求arr所有的子陣列中正數與負數個數相等的最長子陣列長度。
補充題目2:給定一個無序陣列arr,其中元素只是1或0。求arr所有的子陣列中0和1個數相等的最長子陣列長度。
解法:
先定義s的概念,s(i)代表子陣列arr[0...i]所有元素的累加和。那麼子陣列arr[j...i](0<=j<=i<arr.length)的累加和為s(i)-s(j-1),因為根據定義,s(i)= arr[0...i]的累加和=arr[0....j-1]的累加和+arr[j...i]的累加和,又有arr[0...j-1]的累加和為s(j-1)。所以arr[j...i]的累加和為s(i)-s(j-1),這個結論是求解本題的核心。
原問題的解法只遍歷一次arr,具體過程為:
- 設定變數sum=0,表示從0位置開始一直加到i位置所有元素的和。設定變數len=0,表示累加和為k的最長子陣列長度。設定雜湊表map,其中key表示從arr最左邊開始累加的過程中出現過的sum值,對應的value值則表示sum值最早出現的位置。
- 從左到右開始遍歷,遍歷的當前元素為arr[i]。
- 令sum=sum+arr[i],即之前所有元素的累加和為s(i),在map中檢視是否存在sum-k。
- 如果sum-k存在,從map中取出sum-k對應的value值,記為j,j代表從左到右不斷累加的過程中第一次加出sum-k這個累加和的位置。根據之前得出的結論,arr[j+1...i]的累加和為s(i)-s(j),此時s(i)=sum,又有s(j)=sum-k,所以arr[j+1...i]的累加和為k。同時因為map中只記錄每一個累加和最早出現的位置,所以此時的arr[j+1...i]是在必須以arr[i]結尾的所有子陣列中,最長的累加和為k的子陣列,如果該子陣列的長度大於len,就更新len。
- 如果sum-k不存在,說明必須以arr[i]結尾的情況下沒有累加和為k的子陣列。
- 檢查當前的sum(即s(i))是否在map中。如果不存在,說明此時的sum值是第一次出現的,就把記錄(sum,i)加入到map中。如果sum存在,說明之前已經出現過sum,map只記錄一個累加和最早出現的位置,所以此時什麼記錄也不加。
- 令sum=sum+arr[i],即之前所有元素的累加和為s(i),在map中檢視是否存在sum-k。
- 繼續遍歷下一個元素,直到所有的元素遍歷完。
還有一個問題需要處理:根據arr[j+1...i]的累加和為s(i)-s(j),所以,如果從0位置開始累加,會導致j+1>=1。也就是說,所有從0位置開始的子陣列都沒有考慮過。所以,應該從-1位置開始累加,也就是在遍歷之前先把(0,-1)這個記錄放進map,這個記錄的意義是如果任何一個數也不加時,累加和為0,這樣,從0位置開始的子陣列就被我們考慮到了。
明白了原問題的解法,補充問題就可迎刃而解了。第一個補充問題,先把陣列arr中的正數全部1,負數全部變成-1,0不變,然後求累加和為0的最長子陣列長度即可。第二個補充問題,先把陣列arr中的0全部變成-1,1不變,然後求累加和為0的最長子陣列長度即可。
原問題的程式碼如下:
package NowCoder2.Class04;
import java.util.HashMap;
/**
* 求未排序陣列中累加和為給定值的最長子陣列系列問題
*/
public class LongestSumSubArrayLength {
public static int maxLength(int[] arr, int k) {
if (arr == null || arr.length == 0) {
return 0;
}
HashMap<Integer, Integer> map = new HashMap<>();
map.put(0, -1);//重要
int len = 0;
int sum = 0;
for (int i = 0; i < arr.length; i++) {
sum += arr[i];
if (map.containsKey(sum - k)) {
len = Math.max(i - map.get(sum - k), len);
}
if (!map.containsKey(sum)) {
map.put(sum, i);
}
}
return len;
}
/**
* 隨機生成陣列
*
* @param size
* @return
*/
public static int[] generateArray(int size) {
int[] result = new int[size];
for (int i = 0; i != size; i++) {
result[i] = (int) (Math.random() * 11) - 5;
}
return result;
}
/**
* 列印陣列元素
*
* @param arr
*/
public static void printArray(int[] arr) {
for (int i = 0; i != arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
int[] arr = generateArray(20);
printArray(arr);
System.out.println(maxLength(arr, 10));
}
}
題目七:定義陣列的異或和的概念:
陣列中所有的數異或起來,得到的結果叫做陣列的異或和,比如陣列{3,2,1}的異或和是3 ^ 2 ^ 1 = 0
給定一個數組arr,你可以任意把arr分成很多不相容的子陣列,你的目的是:分出來的子陣列中,異或和為0的子陣列最多。
請返回:分出來的子陣列中,異或和為0的子陣列最多是多少?
解答:
本題屬於動態規劃問題。
程式碼:
import java.util.HashMap;
public class Most_EOR {
public static int mostEOR(int[] arr) {
//dp[i]->arr[0~i]這個範圍上,最多劃分出幾個異或和為0的子陣列
int[] dp = new int[arr.length];
HashMap<Integer, Integer> map = new HashMap<>();
map.put(0, -1);//一個數都沒有的時候,異或和為0
int eor_all = arr[0];//0~i 字首異或和
dp[0] = arr[0] == 0 ? 1 : 0; //0~0 答案顯而易見
for (int i = 1; i < arr.length; i++) {
eor_all ^= arr[i];
if (map.containsKey(eor_all)) {
//map.get(eor_all) 就是最後一個有效部分的,前一個位置j
int k = map.get(eor_all); //k+1 ->j ,k最後一個有效部分的前一個位置
dp[i] = k == -1 ? 1 : dp[k] + 1;
}
dp[i] = Math.max(dp[i - 1], dp[i]);
map.put(eor_all, i);
}
return dp[arr.length - 1];
}
}
題目八:給定一個字串str,str表示一個公式,公式裡可能有整數,加減乘除符號和左右括號,返回公式的計算結果。
例如:
STR = “48 *((70-65)-43)+ 8 * 1” 時,返回-1816。
STR =“3 + 1 * 4”,返回7.str = “3+(1 * 4)”,返回7
說明:
- 可以認為給定的字串一定是正確的公式,即不需要對STR做公式有效性檢查。
- 如果是負數,就需要用括號括起來,比如“4 *( - 3)”。但如果負數作為公式的開頭或括號部分的開頭,則可以沒有括號,比如“-3 * 4”和“( - 3 * 4)”都是合法的。
- 不用考慮計算過程中會發生溢位的情況。
思路:本體可以使用遞迴的方法,具體過程如下:
從左到右遍歷str,如果遇到左括號就進入遞迴,相當於將括號裡的內容當成一個新的公式,等括號裡的內容計算完成後將結果返回,此時再接著繼續遍歷str,直到str遍歷完或者遇到右括號,這樣就相當於str中不再包含左右括號。遞迴過程需要返回兩個結果,一個是當前子公式計算的結果,一個是當前遍歷到的str的位置。這樣上級遞迴函式就可以根據這兩個資料繼續向後遍歷。計算公式的結果時,先將乘法和除法計算完,最後再統一計算計算加法和減法。
既然在遞迴過程中遇到‘(’就交給下一層的遞迴過程處理,自己只用接收‘(’和‘)’之間的公式字元子串的結果,所以對所有的遞迴過程來說,可以看作計算的公式都是不含有'('和')'字元的。所以只要想清楚如何計算一個不含有'('和')'的公式字串,整個實現就完成了。
程式碼如下:
package NowCoder2.Class04;
import java.util.Deque;
import java.util.LinkedList;
/**
* 公式字串求值
*/
public class ExpressionCompute {
//公式字串求值
public static int getValue(String exp) {
return value(exp.toCharArray(), 0)[0];
}
private static int[] value(char[] chars, int i) {
Deque<String> deq = new LinkedList<String>();
int pre = 0;
int[] bra = null;
while (i < chars.length && chars[i] != ')') {
if (chars[i] >= '0' && chars[i] <= '9') {
pre = pre * 10 + chars[i++] - '0';
} else if (chars[i] != '(') {
addNum(deq, pre);
deq.addLast(String.valueOf(chars[i++]));
pre = 0;
} else {
bra = value(chars, i + 1);
pre = bra[0];
i = bra[1] + 1;
}
}
addNum(deq, pre);
return new int[]{getNum(deq), i};
}
//計算乘法除法
private static void addNum(Deque<String> deq, int num) {
if (!deq.isEmpty()) {
int cur = 0;
String top = deq.pollLast();
if (top.equals("+") || top.equals("-")) {
deq.addLast(top);
} else {
cur = Integer.valueOf(deq.pollLast());
num = top.equals("*") ? (cur * num) : (cur / num);
}
}
deq.addLast(String.valueOf(num));
}
//計算加法減法
private static int getNum(Deque<String> deq) {
int res = 0;
boolean add = true;
String cur = null;
int num = 0;
while (!deq.isEmpty()) {
cur = deq.pollFirst();
if (cur.equals("+")) {
add = true;
} else if (cur.equals("-")) {
add = false;
} else {
num = Integer.valueOf(cur);
res += add ? num : (-num);
}
}
return res;
}
public static void main(String[] args) {
String exp = "48*((70-65)-43)+8*1";
System.out.println(getValue(exp));
exp = "4*(6+78)+53-9/2+45*8";
System.out.println(getValue(exp));
exp = "10-5*3";
System.out.println(getValue(exp));
exp = "-3*4";
System.out.println(getValue(exp));
exp = "3+1*4";
System.out.println(getValue(exp));
}
}
