【演算法】牛客網演算法進階班(Morris遍歷和sortedMap)
Morris遍歷和sortedMap
介紹一種時間複雜度O(N),額外空間複雜度為O(1)的二叉樹的遍歷方式,N為二叉樹的節點個數
當前節點cur,cur初始時來到head:
- 如果cur沒有左子樹,cur向右移動,cur=cur.right
- 如果cur有左子樹,找到左子樹最右節點,記為mostright
- 如果mostright的右指標指向null,讓它指向cur,然後cur向左移動,cur=cur.left
- 如果mostright的右指標指向cur,讓它指回null,然後cur向右移動,cur=cur.right
Morris遍歷過程中,有左子樹的節點能夠被遍歷兩次,沒有左子樹的節點被遍歷一次
遞迴函式實現先序、中序、後續遍歷的本質是系統棧三次達到每個節點的狀態實現的
Morris遍歷:利用Morris遍歷實現二叉樹的先序、中序、後續遍歷,時間複雜度為O(N),額外空間複雜度為O(1).
思考:Morris遍歷的是指就是避免用棧結構,而是讓下層到上層有指標,具體是通過讓底層節點指向null的空閒指標指回上層的某個節點,從而完成下層到上層的移動。
以Morris中序遍歷的過程為例;
- 假設當前子樹的頭節點為h,讓h的左子樹中最右節點的right指標指向h,然後h的左子樹繼續步驟1的處理過程,直到遇到某一個節點沒有左子樹時記為node,進入步驟2.
- 從node開始通過每個節點的right指標進行移動,並依次列印,假設移動到的節點為cur。對每一個cur節點都判斷cur節點的左子樹中最右節點是否指向cur。
- 如果是,讓cur節點的左子樹中最右節點的right指標指向空,也就是把步驟1的調整後再逐漸調整回來,然後列印cur,繼續通過cur的right指標移動到下一個節點,重複步驟2.
- 如果不是,以cur為頭的子樹重回步驟1執行。
- 步驟2最終移動到null,整個過程結束。
Morris先序遍歷的實現就是Morris中序遍歷實現的簡單改寫。先序遍歷的列印時機放在了步驟2所描述的移動過程中,而先序遍歷只要把列印時機放在步驟1發生的時候即可。步驟1發生的時候,正在處理以h為頭的子樹,並且是以h為頭的子樹首次進入調整過程,此時直接列印h,就可以做到先根列印。
Morris後序遍歷的實現也是Morris中序遍歷實現的改寫,但包含更復雜的調整過程。總的來說,邏輯很簡單,就是依次逆序列印所有節點的左子樹的右邊界,列印的時機放在步驟2的條件1被觸發的時候,也就是調回去的過程發生的時候。
程式碼:
public class MorrisTraversal {
/**
* 使用遞迴的方式實現二叉樹的先序、中序、後序遍歷
* 將列印置於不同位置可以實現不同的遍歷效果
*
* @param head
*/
public static void process(Node head) {
if (head == null) {
return;
}
// 1
//System.out.println(head.value);
process(head.left);
// 2
//System.out.println(head.value);
process(head.right);
// 3
//System.out.println(head.value);
}
public static class Node {
public int value;
Node left;
Node right;
public Node(int data) {
this.value = data;
}
}
/**
* Morris遍歷實現二叉樹的先序遍歷
*
* @param head
*/
public static void morrisIn(Node head) {
if (head == null) {
return;
}
Node cur1 = head;
Node cur2 = null;
while (cur1 != null) {
cur2 = cur1.left;
if (cur2 != null) {
while (cur2.right != null && cur2.right != cur1) {
cur2 = cur2.right;
}
if (cur2.right == null) {//第一次到達有左子樹的節點
cur2.right = cur1;
cur1 = cur1.left;
continue;
} else {
cur2.right = null;
}
}
System.out.print(cur1.value + " ");//將列印語句放在第二次達到有左子樹的節點
cur1 = cur1.right;
}
System.out.println();
}
/**
* Morris遍歷的先序遍歷
*
* @param head
*/
public static void morrisPre(Node head) {
if (head == null) {
return;
}
Node cur1 = head;
Node cur2 = null;
while (cur1 != null) {
cur2 = cur1.left;
if (cur2 != null) {
while (cur2.right != null && cur2.right != cur1) {
cur2 = cur2.right;
}
if (cur2.right == null) {
cur2.right = cur1;
System.out.print(cur1.value + " ");
cur1 = cur1.left;
continue;
} else {
cur2.right = null;
}
} else {
System.out.print(cur1.value + " ");
}
cur1 = cur1.right;
}
System.out.println();
}
/**
* Morris遍歷的後序遍歷
*
* @param head
*/
public static void morrisPos(Node head) {
if (head == null) {
return;
}
Node cur1 = head;
Node cur2 = null;
while (cur1 != null) {
cur2 = cur1.left;
if (cur2 != null) {
while (cur2.right != null && cur2.right != cur1) {
cur2 = cur2.right;
}
if (cur2.right == null) {
cur2.right = cur1;
cur1 = cur1.left;
continue;
} else {
cur2.right = null;
printEdge(cur1.left);
}
}
cur1 = cur1.right;
}
printEdge(head);
System.out.println();
}
public static void printEdge(Node head) {
Node tail = reverseEdge(head);
Node cur = tail;
while (cur != null) {
System.out.print(cur.value + " ");
cur = cur.right;
}
reverseEdge(tail);
}
public static Node reverseEdge(Node from) {
Node pre = null;
Node next = null;
while (from != null) {
next = from.right;
from.right = pre;
pre = from;
from = next;
}
return pre;
}
// for test -- print tree
public static void printTree(Node head) {
System.out.println("Binary Tree:");
printInOrder(head, 0, "H", 17);
System.out.println();
}
public static void printInOrder(Node head, int height, String to, int len) {
if (head == null) {
return;
}
printInOrder(head.right, height + 1, "v", len);
String val = to + head.value + to;
int lenM = val.length();
int lenL = (len - lenM) / 2;
int lenR = len - lenM - lenL;
val = getSpace(lenL) + val + getSpace(lenR);
System.out.println(getSpace(height * len) + val);
printInOrder(head.left, height + 1, "^", len);
}
public static String getSpace(int num) {
String space = " ";
StringBuffer buf = new StringBuffer("");
for (int i = 0; i < num; i++) {
buf.append(space);
}
return buf.toString();
}
public static void main(String[] args) {
Node head = new Node(4);
head.left = new Node(2);
head.right = new Node(6);
head.left.left = new Node(1);
head.left.right = new Node(3);
head.right.left = new Node(5);
head.right.right = new Node(7);
printTree(head);
morrisIn(head);
morrisPre(head);
morrisPos(head);
printTree(head);
}
}
在二叉樹上,何為一個節點的後繼節點?何為搜尋二叉樹?
題目描述:現在有一種新的二叉樹節點型別如下:
public class Node{
public int value;
public Node left;
public Node right;
public Node parent;
public Node(int data){
this.value = data;
}
}該結構比普通二叉樹節點結構多了一個指向父結點的parent指標。假設有一棵Node型別的節點組成的二叉樹,樹中每個節點的parent指標都正確地指向自己的父結點,頭節點的parent指向null。只給一個在二叉樹中的某個節點node,請實現返回node的後繼節點的函式。在二叉樹的中序遍歷的序列中,node的下一個節點叫作node的後繼節點。
思考:簡答的解法:既然新型別的二叉樹節點有指向父節點的指標,那麼一直往上移動,自然可以找到頭節點。找到頭節點之後,再進行二叉樹的中序遍歷,生成中序遍歷序列,然後在這個序列中找到node節點的下一個節點返回即可。如果二叉樹的節點數為N,這種方法要把二叉樹的所有節點至少遍歷一遍,生成中序遍歷的序列還需要大小為N的空間,所以該方法的時間複雜度和空間複雜度都為O(N)。
最優的解法不必遍歷所有的節點,如果node節點和node後繼節點之間的實際距離為L,最優解法只用走過L個節點,時間複雜度為O(L),空間複雜度為O(1)。接下來詳細說明最優解法是如何找到node的後繼節點的。
- 情況1:如果node有右子樹,那麼後繼節點就是右子樹最左邊的節點。
- 情況2:如果node沒有右子樹,那麼先看node是不是node父結點的左孩子,如果是,那麼此時node的父節點就是node的後繼節點;如果是右孩子,就向上尋找node的後繼節點,假設向上移動到的節點記為s,s的父節點記為p,如果發現s是p的左孩子,那麼節點p就是node節點的後繼節點,否則就一直向上移動。
- 情況3:如果在情況2中一直向上尋找,都移動到空節點時還是沒有發現node的後繼節點,說明node根本不存在後繼節點。
程式碼如下:
public Node getNextNode(Node node) {
if (node == null) {
return node;
}
if (node.right != null) { //情況1
return getLeftMost(node.right);
} else { //情況2
Node parent = node.parent;
while (parent != null && parent.left != node) {
node = parent;
parent = node.parent;
}
return parent;
}
}
private Node getLeftMost(Node node) {
if (node == null) {
return node;
}
while (node.left != null) {
node = node.left;
}
return node;
}根據後序陣列重建搜尋二叉樹
題目:給定一個整型陣列arr,已知其中沒有重複值,判斷arr是否可能是節點值型別為整型的搜尋二叉樹後序遍歷的結果。
進階:如果整型陣列arr中沒有重複值,且已知是一棵搜尋二叉樹的後序遍歷結果,通過陣列arr重構二叉樹。
解法:原問題的解法:二叉樹的後序遍歷為先左、再右,最後根的順序,所以,如果一個數組是二叉樹後序遍歷結果,那麼頭節點的值一定會是陣列的最後一個元素。搜尋二叉樹的性質,所有比後序陣列最後一個元素值小的陣列會在陣列的左邊,比陣列最後一個元素值大的陣列會在陣列的右邊。如果不滿足這種情況,說明這個陣列一定不可能是搜尋二叉樹後續遍歷的結果,接下來陣列劃分成左邊陣列和右邊陣列,相當於二叉樹分出了左子樹和右子樹,只要遞迴地進行如上判斷即可。
程式碼:
/**
* 根據後序陣列重建搜尋二叉樹
*/
public class IsPostArray {
public boolean isPostArray(int[] arr) {
if (arr == null || arr.length == 0) {
return false;
}
return isPost(arr, 0, arr.length - 1);
}
public boolean isPost(int[] arr, int start, int end) {
if (start == end) {
return true;
}
int less = -1;
int more = end;
for (int i = start; i < end; i++) {
if (arr[end] > arr[i]) {
less = i;
} else {
more = more == end ? i : more;
}
}
if (less == -1 || more == end) {
return isPost(arr, start, end - 1);
}
if (less != more - 1) {
return false;
}
return isPost(arr, start, less) && isPost(arr, more, end - 1);
}
}
進階問題的分析與原問題同理,一棵樹的後序陣列中最後一個值為二叉樹頭節點的陣列左部分都比頭節點的值小,用來生成頭節點的左子樹,剩下的部分用來生成右子樹。
/**
* 已知一棵搜尋二叉樹的後序遍歷結果,通過陣列arr重構二叉樹
*/
public class PosArrayToBST {
public class Node {
public int value;
public Node left;
public Node right;
public Node(int value) {
this.value = value;
}
}
public Node posArrayToBST(int[] posArr) {
if (posArr == null) {
return null;
}
return posToBST(posArr, 0, posArr.length - 1);
}
private Node posToBST(int[] posArr, int start, int end) {
if (start > end) {
return null;
}
Node head = new Node(posArr[end]);
int less = -1;
int more = end;
for (int i = start; i < end; i++) {
if (posArr[end] > posArr[i]) {
less = i;
} else {
more = more == end ? i : more;
}
}
head.left = posToBST(posArr, start, less);
head.right = posToBST(posArr, more, end - 1);
return head;
}
}
如何實現搜尋二叉樹的查詢?插入?刪除?
定義:二叉搜尋樹是這樣的一種二叉樹:
(1)每個元素都有一個關鍵值,並且沒有任意兩個元素有相同的關鍵值
(2)根節點的左子樹中任意元素的關鍵值小於根節點的關鍵值。
(3)根節點的右子樹中任意元素的關鍵值大於根節點的關鍵值。
(4)根節點的左右子樹也是二叉搜尋樹。
從定義看出,二叉搜尋樹是一種特殊的二叉樹,它給每個元素加上了序的概念,但又不同於最大最小堆,它總是 左<根<右的。
查詢:
從根元素開始遍歷,如果找到匹配的,則直接將其對應元素的值返回。
如果關鍵值比當前查詢元素的關鍵值小,那麼關鍵值一定在左子樹中,所以遞迴的在左子樹中查詢。
如果關鍵值比當前查詢元素的關鍵值大,那麼關鍵值一定在右子樹中,所以遞迴的在右子樹中查詢。
上述遞迴跳出的條件就是當前查詢元素為空,一旦為空都找不到匹配,則說明該二叉搜尋樹中沒有匹配值。
插入:
插入之前必須保證二叉搜尋樹的第一條定義,所以先找下是否有匹配元素,如果有,則不執行插入動作。
然後從根開始折半找,根據子元素的值來確定這個值插入左邊還是右邊,直到選擇到一個精確的位置,使得待插元素的關鍵值剛好落在當前元素和其某個子元素之間(或者沒有子元素)
刪除:
刪除複雜多了,先遍歷找到要刪除的元素,
分為3種情況:
- 如果該元素左,右子樹都不為空,則把該元素替換為其左子樹中的最大元素或者右子樹的最小元素(因為這2個元素剛好是與當前元素最近的2個元素)
- 如果該元素左,右子樹都為空( 也就是葉節點),那麼直接丟棄,當然也要考慮根節點的情況。
- 如果該元素左或者右子樹不為空,那麼需要找到該元素的父親元素,然後把其不為空的這個分支的根元素設為父親元素的直接子元素,當然也要考慮根節點的情況。
public class AbstractBinarySearchTree {
public static class Node {
public Integer value;
public Node parent;
public Node left;
public Node right;
public Node(Integer value, Node parent, Node left, Node right) {
super();
this.value = value;
this.parent = parent;
this.left = left;
this.right = right;
}
public boolean isLeaf() {
return left == null && right == null;
}
@Override
public int hashCode() {
final int prime = 31;
int result = 1;
result = prime * result + ((value == null) ? 0 : value.hashCode());
return result;
}
@Override
public boolean equals(Object obj) {
if (this == obj)
return true;
if (obj == null)
return false;
if (getClass() != obj.getClass())
return false;
Node other = (Node) obj;
if (value == null) {
if (other.value != null)
return false;
} else if (!value.equals(other.value))
return false;
return true;
}
}
/**
* 整個樹開始的根節點.
*/
public Node root;
/**
* 樹的大小.
*/
protected int size;
/**
* 因為這是抽象類,並且各種樹在不同節點上具有不同的附加資訊,
* 所以子類使用該抽象方法來建立節點。
* (maybe of class {@link Node} or maybe some
* different node sub class).
*
* @param value Value that node will have.
* @param parent Node's parent.
* @param left Node's left child.
* @param right Node's right child.
* @return Created node instance.
*/
protected Node createNode(int value, Node parent, Node left, Node right) {
return new Node(value, parent, left, right);
}
/**
* 查詢具有特定值的節點。 如果未找到,則返回null。
*
* @param element Element value.
* @return Node with value provided, or null if not found.
*/
public Node search(int element) {
Node node = root;
while (node != null && node.value != null && node.value != element) {
if (element < node.value) {
node = node.left;
} else {
node = node.right;
}
}
return node;
}
/**
* 插入新元素.
*
* @param element Element to insert.
*/
public Node insert(int element) {
if (root == null) {
root = createNode(element, null, null, null);
size++;
return root;
}
Node insertParentNode = null;
Node searchTempNode = root;
while (searchTempNode != null && searchTempNode.value != null) {
insertParentNode = searchTempNode;
if (element < searchTempNode.value) {
searchTempNode = searchTempNode.left;
} else {
searchTempNode = searchTempNode.right;
}
}
Node newNode = createNode(element, insertParentNode, null, null);
if (insertParentNode.value > newNode.value) {
insertParentNode.left = newNode;
} else {
insertParentNode.right = newNode;
}
size++;
return newNode;
}
/**
* 如果存在具有此值的節點,則刪除元素.
*
* @param element Element value to remove.
* @return New node that is in place of deleted node. Or null if element for
* delete was not found.
*/
public Node delete(int element) {
Node deleteNode = search(element);
if (deleteNode != null) {
return delete(deleteNode);
} else {
return null;
}
}
/**
* 找到節點時刪除邏輯.
*
* @param deleteNode Node that needs to be deleted.
* @return 用於替換已刪除節點的新節點。 如果未找到要刪除的元素,則返回null。
*/
protected Node delete(Node deleteNode) {
if (deleteNode != null) {
Node nodeToReturn = null;
if (deleteNode != null) {
if (deleteNode.left == null) {
nodeToReturn = transplant(deleteNode, deleteNode.right);
} else if (deleteNode.right == null) {
nodeToReturn = transplant(deleteNode, deleteNode.left);
} else {
Node successorNode = getMinimum(deleteNode.right);
if (successorNode.parent != deleteNode) {
transplant(successorNode, successorNode.right);
successorNode.right = deleteNode.right;
successorNode.right.parent = successorNode;
}
transplant(deleteNode, successorNode);
successorNode.left = deleteNode.left;
successorNode.left.parent = successorNode;
nodeToReturn = successorNode;
}
size--;
}
return nodeToReturn;
}
return null;
}
/**
* 將一個節點從樹(newNode)放到另一個節點(nodeToReplace).
*
* @param nodeToReplace Node which is replaced by newNode and removed from tree.
* @param newNode New node.
* @return New replaced node.
*/
private Node transplant(Node nodeToReplace, Node newNode) {
if (nodeToReplace.parent == null) {
this.root = newNode;
} else if (nodeToReplace == nodeToReplace.parent.left) {
nodeToReplace.parent.left = newNode;
} else {
nodeToReplace.parent.right = newNode;
}
if (newNode != null) {
newNode.parent = nodeToReplace.parent;
}
return newNode;
}
/**
* @param element
* @return true if tree contains element.
*/
public boolean contains(int element) {
return search(element) != null;
}
/**
* @return Minimum element in tree.
*/
public int getMinimum() {
return getMinimum(root).value;
}
/**
* @return Maximum element in tree.
*/
public int getMaximum() {
return getMaximum(root).value;
}
/**
* Get next element element who is bigger than provided element.
*
* @param element Element for whom descendand element is searched
* @return Successor value.
*/
// TODO Predecessor
public int getSuccessor(int element) {
return getSuccessor(search(element)).value;
}
/**
* @return Number of elements in the tree.
*/
public int getSize() {
return size;
}
/**
* Tree traversal with printing element values. In order method.
*/
public void printTreeInOrder() {
printTreeInOrder(root);
}
/**
* Tree traversal with printing element values. Pre order method.
*/
public void printTreePreOrder() {
printTreePreOrder(root);
}
/**
* Tree traversal with printing element values. Post order method.
*/
public void printTreePostOrder() {
printTreePostOrder(root);
}
/*-------------------PRIVATE HELPER METHODS-------------------*/
private void printTreeInOrder(Node entry) {
if (entry != null) {
printTreeInOrder(entry.left);
if (entry.value != null) {
System.out.println(entry.value);
}
printTreeInOrder(entry.right);
}
}
private void printTreePreOrder(Node entry) {
if (entry != null) {
if (entry.value != null) {
System.out.println(entry.value);
}
printTreeInOrder(entry.left);
printTreeInOrder(entry.right);
}
}
private void printTreePostOrder(Node entry) {
if (entry != null) {
printTreeInOrder(entry.left);
printTreeInOrder(entry.right);
if (entry.value != null) {
System.out.println(entry.value);
}
}
}
protected Node getMinimum(Node node) {
while (node.left != null) {
node = node.left;
}
return node;
}
protected Node getMaximum(Node node) {
while (node.right != null) {
node = node.right;
}
return node;
}
protected Node getSuccessor(Node node) {
// 如果有右子樹,則後繼是該子樹的最左邊節點
if (node.right != null) {
return getMinimum(node.right);
} else { // 否則它是最低的祖先,其左孩子也是節點的祖先
Node currentNode = node;
Node parentNode = node.parent;
while (parentNode != null && currentNode == parentNode.right) {
// 直到我們發現父節點currentNode不在右子樹中。
currentNode = parentNode;
parentNode = parentNode.parent;
}
return parentNode;
}
}
// -------------------------------- TREE PRINTING
// ------------------------------------
public void printTree() {
printSubtree(root);
}
public void printSubtree(Node node) {
if (node.right != null) {
printTree(node.right, true, "");
}
printNodeValue(node);
if (node.left != null) {
printTree(node.left, false, "");
}
}
private void printNodeValue(Node node) {
if (node.value == null) {
System.out.print("<null>");
} else {
System.out.print(node.value.toString());
}
System.out.println();
}
private void printTree(Node node, boolean isRight, String indent) {
if (node.right != null) {
printTree(node.right, true, indent + (isRight ? " " : " | "));
}
System.out.print(indent);
if (isRight) {
System.out.print(" /");
} else {
System.out.print(" \\");
}
System.out.print("----- ");
printNodeValue(node);
if (node.left != null) {
printTree(node.left, false, indent + (isRight ? " | " : " "));
}
}
}
擴充套件:
- 如何實現在搜尋二叉樹上查詢與給定值aim最近的值
- 如何實現在搜尋二叉樹上查詢<=給定值aim最近的值
- 如何實現在搜尋二叉樹上查詢>=給定值aim最近的值
思考:
問題1:使用遞迴查詢,如果當前節點值小於目標值,則結果只可能是當前節點值或者右子樹中的值;如果當前節點值大於目標值,則結果只可能是當前節點值或者左子樹中的值。
程式碼:
/**
* 二叉搜尋樹最接近值查詢
*/
public class ClosestValue {
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
private int value;
public int closestValue(TreeNode root, double target) {
if (root.val == target)
return root.val;
if (root.val < target) {
if (root.right == null)
return root.val;
int right = closestValue(root.right, target);
if (Math.abs(root.val - target) <= Math.abs(right - target))
return root.val;
return right;
} else {
if (root.left == null)
return root.val;
int left = closestValue(root.left, target);
if (Math.abs(root.val - target) <= Math.abs(left - target))
return root.val;
return left;
}
}
}
問題2:同理,如果在二叉搜尋樹中查詢小於等於aim的最大值,則
- 如果當前節點值等於目標值,則返回該節點的值
- 如果當前節點值小於目標值,則結果只可能是當前節點值或者其存在於其左子樹中
- 如果當前節點值大於目標值,則結果只可能存在與其左子樹中
程式碼:
/**
* 在二叉搜尋樹中找最大的小於某個key值的節點
* 迭代實現
*
* @param root
* @param key
* @return
*/
public TreeNode FindCeiling3(TreeNode root, int key) {
TreeNode ceiling = null;
TreeNode current = root;
while (current != null) {
if (current.val >= key) {
current = current.left;
} else {
ceiling = current;
current = current.right;
}
}
return ceiling;
}問題3:如果在二叉搜尋樹中查詢大於等於aim的最小值,則
- 如果當前節點值等於目標值,則返回該節點的值
- 如果當前節點值小於目標值,則結果只可能存在於其右子樹中
- 如果當前節點值大於目標值,則結果只可能是當前節點值或者其左子樹中的值。
程式碼:
/**
* 在二叉搜尋樹中找最小的大於某個key值的節點
* 迭代實現
*
* @param root
* @param key
* @return
*/
public TreeNode FindCeiling1(TreeNode root, int key) {
TreeNode ceiling = null;
TreeNode current = root;
while (current != null) {
if (current.val <= key) {
current = current.right;
} else {
ceiling = current;
current = current.left;
}
}
return ceiling;
}
/**
* 遞迴實現
*
* @param root
* @param key
* @return
*/
public TreeNode FindCeiling2(TreeNode root, int key) {
if (root == null) {
return root;
}
if (root.val <= key) {
return FindCeiling2(root.right, key);
} else {
TreeNode ceiling = FindCeiling2(root.left, key);
return ceiling != null ? ceiling : root;
}
}判斷一棵二叉樹是否為平衡二叉樹
題目:平衡二叉樹的性質為:要麼是一棵空樹,要麼任何一個節點的左右子樹高度差的絕對值不超過1.給定一棵二叉樹的頭節點head,判斷這棵二叉樹是否為平衡二叉樹。
要求:如果二叉樹的節點數為N,要求時間複雜度為O(N)。
解法:解法的整體過程為二叉樹的後序遍歷,對任何一個節點node來說,先遍歷node的左子樹,遍歷過程中收集兩個資訊,node的左子樹是否為平衡二叉樹,node的左子樹最深到哪一層記為lH。如果發現node的左子樹不是平衡二叉樹,無序進行任何後續過程,此時返回什麼已不重要,因為已經發現整棵樹不是平衡二叉樹,退出遍歷過程;如果node的左子樹是平衡二叉樹,再遍歷node的右子樹,遍歷過程中再收集兩個資訊,node的右子樹是否為平衡二叉樹,node的右子樹最深到哪一層記為rH。如果發現node的右子樹不是平衡二叉樹,無須進行任何後續過程,返回什麼也不重要,因為已經發現整棵樹不是平衡二叉樹,退出遍歷過程;如果node的右子樹也是平衡二叉樹,就看lH和rH差的絕對值是否大於1,如果大於1,說明已經發現整棵樹不是平衡二叉樹,如果不大於1,則返回lH和rH較大的一個。
程式碼:
public class IsBalance {
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public boolean isBalance(TreeNode head) {
boolean[] res = new boolean[1];
res[0] = true;
getHeight(head, 1, res);
return res[0];
}
/**
* 一旦發現不符合平衡二叉樹的性質,遞迴過程會迅速推出
* 整個後序遍歷的過程中,每個節點最多遍歷一次,如果中途發現不滿足平衡二叉樹的性質,整個過程會迅速退出,沒遍歷的節點也不用遍歷了,
* 所以時間複雜度為O(N)
*
* @param head
* @param level
* @param res 長度為1,功能相當於一個全域性的Boolean變數
* @return
*/
private int getHeight(TreeNode head, int level, boolean[] res) {
if (head == null) {
return level;
}
int lH = getHeight(head.left, level + 1, res);
if (!res[0]) {
return level;
}
int rH = getHeight(head.right, level + 1, res);
if (!res[0]) {
return level;
}
if (Math.abs(lH - rH) > 1) {
res[0] = false;
}
return Math.max(lH, rH);
}
}
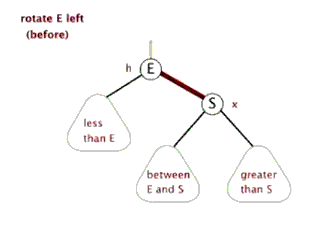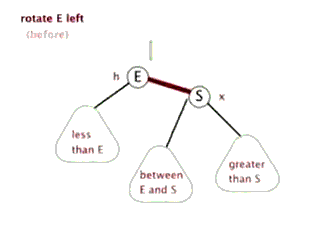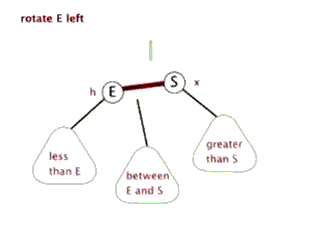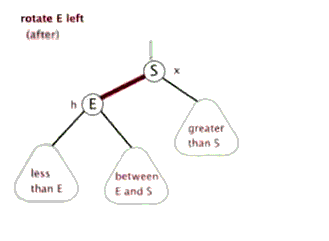
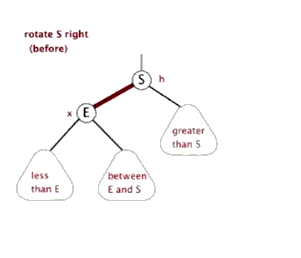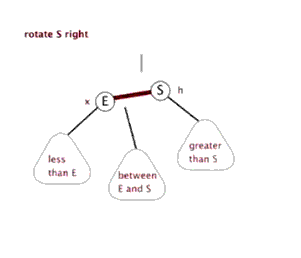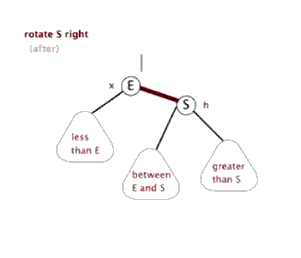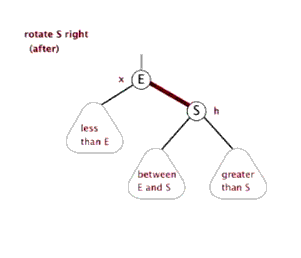
樹的左旋與右旋
- 介紹調整樹的左旋操作
- 介紹調整樹的右旋操作
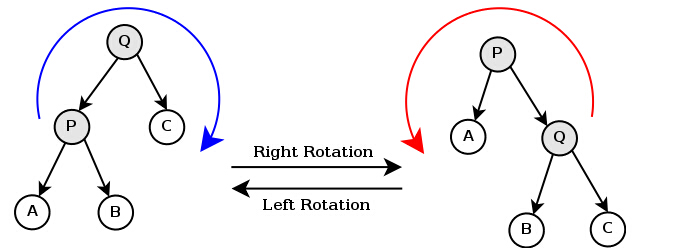
思考:如下圖所示的操作中,對節點Q的操作為右旋,對節點P的操作為左旋,二者互為逆操作。簡單地講:
- 右旋:自己變為左孩子的右孩子
- 左旋:自己變為右孩子的左孩子
程式碼:
public class BinTree {
/**
* 定義二叉樹節點
*/
private class Node {
int val;
Node lchild;
Node rchild;
Node parent;
Node(int data) {
this.val = data;
}
}
public Node root;//根節點
public void rightRotate(Node node) {
Node p = node.lchild;
Node b = p.rchild;
Node fa = node.parent;
b.parent = node;
node.lchild = b;
node.parent = p;
p.rchild = node;
if (root == node) {
root = p;
} else {
p.parent = fa;
if (fa.lchild == node)
fa.lchild = p;
else
fa.rchild = p;
}
}
public void leftRoate(Node node) {
Node q = node.rchild;
Node b = q.lchild;
Node fa = node.parent;
b.parent = node;
node.rchild = b;
node.parent = q;
q.lchild = node;
if (node == root) {
root = node;
} else {
q.parent = fa;
if (fa.lchild == node)
fa.lchild = q;
else
fa.rchild = q;
}
}
}
#include
class BinTree{
private:
typedef struct node{
int data;
node*lchild,*rchild,*parent;
}*tree;
tree root;
public:
void right_rotate(node *p);
void left_rotate(node *p);
};
void BinTree::right_rotate(node *q){
node* p=q->lchild;
node* b=p->rchild;
node* fa=q->parent;
b->parent=q;
q->lchild=b;
q->parent=p;
p->rchild=q;
if(q==root)
root=p;//此時p->parent==q 但沒關係,已經標記了根為p
else{
p->parent=fa;
if(fa->lchild==q) fa->lchild=p;
else fa->rchild=p;
}
}
void BinTree::left_rotate(node *p){
tree q=p->rchild;
tree b=q->lchild;
node* fa=p->parent;
b->parent=p;
p->rchild=b;
p->parent=q;
q->lchild=p;
if(p==root)
root=q;//此時q->parent==p 但沒關係,已經標記了根為q
else{
q->parent=fa;
if(fa->lchild==p) fa->lchild=q;
else fa->rchild=q;
}
}
/**
* Abstract class for self balancing binary search trees. Contains some methods
* that is used for self balancing trees.
*
* @author Ignas Lelys
* @created Jul 24, 2011
*/
public abstract class AbstractSelfBalancingBinarySearchTree extends AbstractBinarySearchTree {
/**
* Rotate to the left.
* 左旋
*
* @param node Node on which to rotate.
* @return Node that is in place of provided node after rotation.
*/
protected Node rotateLeft(Node node) {
Node temp = node.right;
temp.parent = node.parent;
node.right = temp.left;
if (node.right != null) {
node.right.parent = node;
}
temp.left = node;
node.parent = temp;
// temp took over node's place so now its parent should point to temp
if (temp.parent != null) {
if (node == temp.parent.left) {
temp.parent.left = temp;
} else {
temp.parent.right = temp;
}
} else {
root = temp;
}
return temp;
}
/**
* Rotate to the right.
* 右旋
*
* @param node Node on which to rotate.
* @return Node that is in place of provided node after rotation.
*/
protected Node rotateRight(Node node) {
Node temp = node.left;
temp.parent = node.parent;
node.left = temp.right;
if (node.left != null) {
node.left.parent = node;
}
temp.right = node;
node.parent = temp;
// temp took over node's place so now its parent should point to temp
if (temp.parent != null) {
if (node == temp.parent.left) {
temp.parent.left = temp;
} else {
temp.parent.right = temp;
}
} else {
root = temp;
}
return temp;
}
}
介紹AVL樹
- 當插入或刪除一個節點時,可能會讓整棵AVL不平衡。此時,只需要把最小不平衡子樹調整即可恢復整體的平衡性。
- 介紹樹的LL,RR,LR,RL調整
- 介紹插入節點時的調整細節
- 介紹刪除節點時的調整細節
AVL樹是帶有平衡條件的二叉查詢樹。這個平衡條件必須容易保持,而且它保證樹的深度必須是O(log N)。一顆AVL樹是其每個節點的左子樹和右子樹的高度最多差1的二叉查詢樹(空樹的高度定義為-1)。對AVL樹進行插入操作可能會使其失去平衡的條件,但這可以通過對樹進行簡單的修正來保持其平衡的屬性,這種操作稱之為旋轉。
一顆平衡二叉樹,如果有n個結點,其高度可保持O(log2^n),平均搜尋長度也可以保持在O(log2^n)
平衡化旋轉 AVL樹相較於普通的二叉搜尋樹,最主要的就是做了平衡化處理,使得二叉樹變的平衡,高度降低。 在插入一個結點後應該沿搜尋路徑將路徑上的結點平衡因子進行修改,當平衡因子大於1時,就需要進行平衡化處理。從發生不平衡的結點起,沿剛才回溯的路徑取直接下兩層的結點,如果這三個結點在一條直線上,則採用單旋轉進行平衡化,如果這三個結點位於一條折線上,則採用雙旋轉進行平衡化。 單旋轉
- 左單旋
如下圖的動畫演示:將右子樹的左子樹連結到父結點的右孩子節點,父結點作為ptr節點的左孩子節點便完成了旋轉。
- 右單旋
如下圖動畫演示:右單旋是左單旋的映象旋轉,當前節點ptr,與父結點和當前節點的左孩子節點位於一條直線上時,使用右單旋進行平衡。
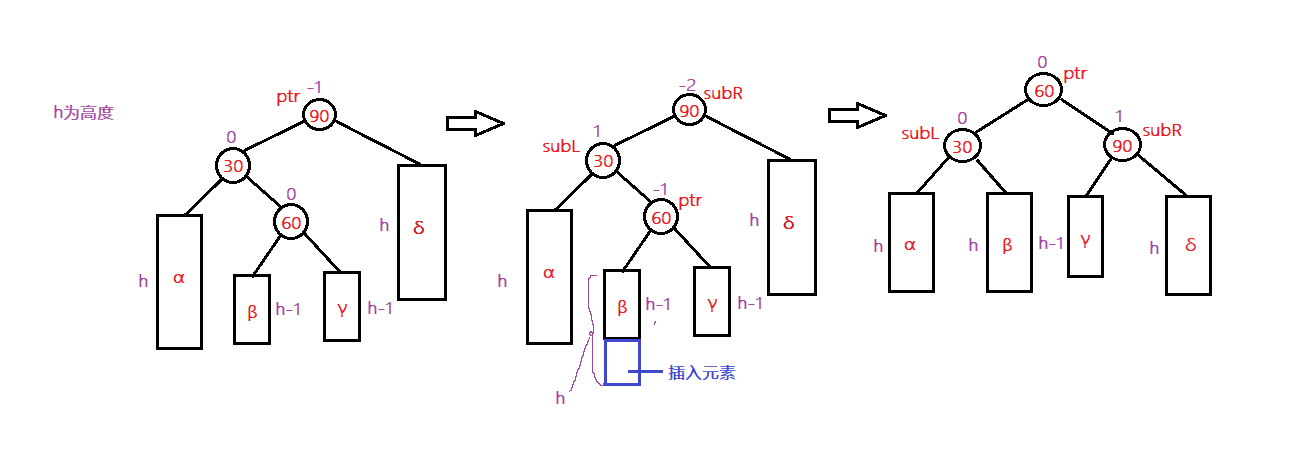
雙旋轉
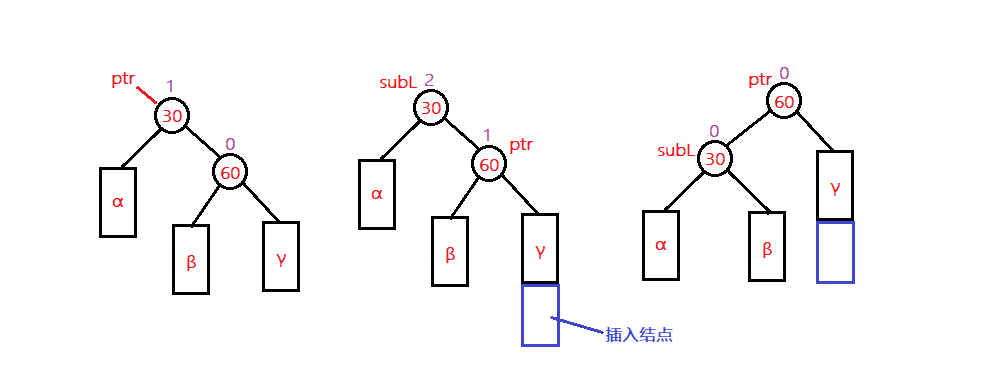
當在ptr的左子樹的右子樹中插入一個結點後,造成了ptr平衡因子為-2的不平衡,將ptr向下找到當前節點的左孩子的右孩子,先進行左單旋ptr->left=subL,然後將ptr的右子樹斷開指向subR,此時便完成了旋轉,最後將平衡因子進行更新。
分為先右單旋再左單旋和先左單旋後右單旋兩種方式,互為映象旋轉。
詳細過程的程式碼如下
/**
* AVL tree implementation.
*
* In computer science, an AVL tree is a self-balancing binary search tree, and
* it was the first such data structure to be invented.[1] In an AVL tree, the
* heights of the two child subtrees of any node differ by at most one. Lookup,
* insertion, and deletion all take O(log n) time in both the average and worst
* cases, where n is the number of nodes in the tree prior to the operation.
* Insertions and deletions may require the tree to be rebalanced by one or more
* tree rotations.
*
* @author Ignas Lelys
* @created Jun 28, 2011
*
*/
public class AVLTree extends AbstractSelfBalancingBinarySearchTree {
/**
* @see trees.AbstractBinarySearchTree#insert(int)
*
* AVL tree insert method also balances tree if needed. Additional
* height parameter on node is used to track if one subtree is higher
* than other by more than one, if so AVL tree rotations is performed
* to regain balance of the tree.
*/
@Override
public Node insert(int element) {
Node newNode = super.insert(element);
rebalance((AVLNode)newNode);
return newNode;
}
/**
* @see trees.AbstractBinarySearchTree#delete(int)
*/
@Override
public Node delete(int element) {
Node deleteNode = super.search(element);
if (deleteNode != null) {
Node successorNode = super.delete(deleteNode);
if (successorNode != null) {
// if replaced from getMinimum(deleteNode.right) then come back there and update heights
AVLNode minimum = successorNode.right != null ? (AVLNode)getMinimum(successorNode.right) : (AVLNode)successorNode;
recomputeHeight(minimum);
rebalance((AVLNode)minimum);
} else {
recomputeHeight((AVLNode)deleteNode.parent);
rebalance((AVLNode)deleteNode.parent);
}
return successorNode;
}
return null;
}
/**
* @see trees.AbstractBinarySearchTree#createNode(int, trees.AbstractBinarySearchTree.Node, trees.AbstractBinarySearchTree.Node, trees.AbstractBinarySearchTree.Node)
*/
@Override
protected Node createNode(int value, Node parent, Node left, Node right) {
return new AVLNode(value, parent, left, right);
}
/**
* Go up from inserted node, and update height and balance informations if needed.
* If some node balance reaches 2 or -2 that means that subtree must be rebalanced.
*
* @param node Inserted Node.
*/
private void rebalance(AVLNode node) {
while (node != null) {
Node parent = node.parent;
int leftHeight = (node.left == null) ? -1 : ((AVLNode) node.left).height;
int rightHeight = (node.right == null) ? -1 : ((AVLNode) node.right).height;
int nodeBalance = rightHeight - leftHeight;
// rebalance (-2 means left subtree outgrow, 2 means right subtree)
if (nodeBalance == 2) {
if (node.right.right != null) {
node = (AVLNode)avlRotateLeft(node); //左單旋
break;
} else {
node = (AVLNode)doubleRotateRightLeft(node); //先右旋後左旋的雙旋轉
break;
}
} else if (nodeBalance == -2) {
if (node.left.left != null) {
node = (AVLNode)avlRotateRight(node); //右單旋
break;
} else {
node = (AVLNode)doubleRotateLeftRight(node); //先左旋後右旋的雙旋轉
break;
}
} else {
updateHeight(node);
}
node = (AVLNode)parent;
}
}
/**
* Rotates to left side.左單旋
*/
private Node avlRotateLeft(Node node) {
Node temp = super.rotateLeft(node);
updateHeight((AVLNode)temp.left);
updateHeight((AVLNode)temp);
return temp;
}
/**
* Rotates to right side.右單旋
*/
private Node avlRotateRight(Node node) {
Node temp = super.rotateRight(node);
updateHeight((AVLNode)temp.right);
updateHeight((AVLNode)temp);
return temp;
}
/**
* Take right child and rotate it to the right side first and then rotate
* node to the left side.
* 先右旋後左旋
*/
protected Node doubleRotateRightLeft(Node node) {
node.right = avlRotateRight(node.right);
return avlRotateLeft(node);
}
/**
* Take right child and rotate it to the right side first and then rotate
* node to the left side.
* 先左旋後右旋
*/
protected Node doubleRotateLeftRight(Node node) {
node.left = avlRotateLeft(node.left);
return avlRotateRight(node);
}
/**
* Recomputes height information from the node and up for all of parents.
* It needs to be done after delete.
*/
private void recomputeHeight(AVLNode node) {
while (node != null) {
node.height = maxHeight((AVLNode)node.left, (AVLNode)node.right) + 1;
node = (AVLNode)node.parent;
}
}
/**
* Returns higher height of 2 nodes.
*/
private int maxHeight(AVLNode node1, AVLNode node2) {
if (node1 != null && node2 != null) {
return node1.height > node2.height ? node1.height : node2.height;
} else if (node1 == null) {
return node2 != null ? node2.height : -1;
} else if (node2 == null) {
return node1 != null ? node1.height : -1;
}
return -1;
}
/**
* Updates height and balance of the node.
*
* @param node Node for which height and balance must be updated.
*/
private static final void updateHeight(AVLNode node) {
int leftHeight = (node.left == null) ? -1 : ((AVLNode) node.left).height;
int rightHeight = (node.right == null) ? -1 : ((AVLNode) node.right).height;
node.height = 1 + Math.max(leftHeight, rightHeight);
}
/**
* Node of AVL tree has height and balance additional properties. If balance
* equals 2 (or -2) that node needs to be re balanced. (Height is height of
* the subtree starting with this node, and balance is difference between
* left and right nodes heights).
*
* @author Ignas Lelys
* @created Jun 30, 2011
*
*/
protected static class AVLNode extends Node {
public int height;
public AVLNode(int value, Node parent, Node left, Node right) {
super(value, parent, left, right);
}
}
}
何為紅黑樹?
紅黑樹的定義是含有紅黑連線並滿足下列條件的二叉查詢樹:
- 紅連結均為左連結
- 沒有任何一個結點同時和兩條紅連結相連
- 該樹是完美黑色平衡的,即任意空連結到根結點的路徑上的黑連結數量相同。
上述定義摘自《演算法》第四版
R-B Tree,全稱是Red-Black Tree,又稱為“紅黑樹”,它一種特殊的二叉查詢樹。紅黑樹的每個節點上都有儲存位表示節點的顏色,可以是紅(Red)或黑(Black)。
紅黑樹的特性:
(1)每個節點或者是黑色,或者是紅色。 (2)根節點是黑色。 (3)每個葉子節點(NIL)是黑色。 [注意:這裡葉子節點,是指為空(NIL或NULL)的葉子節點!] (4)如果一個節點是紅色的,則它的子節點必須是黑色的。 (5)從一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑節點。
注意: (01) 特性(3)中的葉子節點,是隻為空(NIL或null)的節點。 (02) 特性(5),確保沒有一條路徑會比其他路徑長出倆倍。因而,紅黑樹是相對是接近平衡的二叉樹。
紅黑樹示意圖如下:
何為SB樹?
每棵子樹的大小,不小於其兄弟的子樹大小(即每棵叔叔樹的大小,不小於侄子樹的大小)。(陳啟峰發明與2006年底完成的論文《Size Balanced Tree》,並在2007年的全國青少年資訊學奧林匹克競賽冬令營中發表)