# 匯入模組，並重命名為np
import numpy as np
# 單個列表建立一維陣列
arr1 = np.array([3,10,8,7,34,11,28,72])
print('一維陣列：\n',arr1)
# 一維陣列元素的獲取
print(arr1[[2,3,5,7]])

# 巢狀元組建立二維陣列
arr2 = np.array(((8.5,6,4.1,2,0.7),(1.5,3,5.4,7.3,9),(3.2,3,3.8,3,3),(11.2,13.4,15.6,17.8,19)))
print('二維陣列：\n',arr2)
# 二維陣列元素的獲取
# 第2行第3列元素
print(arr2[1,2])
# 第3行所有元素
print(arr2[2,:])
# 第2列所有元素
print(arr2[:,1])
# 第2至4行，2至5行
print(arr2[1:4,1:5])
# 第一行、最後一行和第二列、第四列構成的陣列
print(arr2[[0,-1],[1,3]])
# 第一行、最後一行和第一列、第三列、第四列構成的陣列
print(arr2[[0,-1,0],[1,2,3]])
# 第一行、最後一行和第二列、第四列構成的陣列
print(arr2[np.ix_([0,-1],[1,3])])
# 第一行、最後一行和第一列、第三列、第四列構成的陣列
print(arr2[np.ix_([0,-1],[1,2,3])])

# 讀入資料
stu_score = np.genfromtxt(fname = r'F:\\python_Data_analysis_and_mining\\04\\stu_socre.txt',delimiter='\t',skip_header=1)
# 檢視資料結構
print(type(stu_score))
# 檢視資料維數
print(stu_score.ndim)
# 檢視資料行列數
print(stu_score.shape)
# 檢視陣列元素的資料型別
print(stu_score.dtype)
# 檢視陣列元素個數
print(stu_score.size)

arr3 = np.array([[1,5,7],[3,6,1],[2,4,8],[5,8,9],[1,5,9],[8,5,2]])
# 陣列的行列數
print(arr3.shape)
# 使用reshape方法更改陣列的形狀
print(arr3.reshape(2,9))
# 列印陣列arr3的行列數
print(arr3.shape)

arr4 = np.array([[1,10,100],[2,20,200],[3,30,300]])
print('原陣列：\n',arr4)
# 預設排序降維
print('陣列降維：\n',arr4.ravel())
print(arr4.flatten())
print(arr4.reshape(-1))
# 改變排序模式的降維
print(arr4.ravel(order = 'F'))
print(arr4.flatten(order = 'F'))
print(arr4.reshape(-1, order = 'F'))
# 更改預覽值
arr4.flatten()[0] = 2000
print('flatten方法：\n',arr4)
arr4.ravel()[1] = 1000
print('ravel方法：\n',arr4)
arr4.reshape(-1)[2] = 3000
print('reshape方法：\n',arr4)

arr4 = np.array([[1,10,100],[2,20,200],[3,30,300]])
arr5 = np.array([1,2,3])
print(arr4)
print(arr5)
print('vstack縱向合併陣列：\n',np.vstack([arr4,arr5]))
print('row_stack縱向合併陣列：\n',np.row_stack([arr4,arr5]))
arr6 = np.array([[5],[15],[25]])
print('hstack橫向合併陣列：\n',np.hstack([arr4,arr6]))
print('column_stack橫向合併陣列：\n',np.column_stack([arr4,arr6]))
print(arr4)
print('垂直方向計算陣列的和：\n',np.sum(arr4,axis = 0))
print('水平方向計算陣列的和：\n',np.sum(arr4, axis = 1))

# 加法運算
math = np.array([98,83,86,92,67,82])
english = np.array([68,74,66,82,75,89])
chinese = np.array([92,83,76,85,87,77])
tot_symbol = math+english+chinese
tot_fun = np.add(np.add(math,english),chinese)
print('符號加法：\n',tot_symbol)
print('函式加法：\n',tot_fun)

# 除法運算
height = np.array([165,177,158,169,173])
weight = np.array([62,73,59,72,80])
BMI_symbol = weight/(height/100)**2
BMI_fun = np.divide(weight,np.divide(height,100)**2)
print('符號除法：\n',BMI_symbol)
print('函式除法：\n',BMI_fun)

arr7 = np.array([[1,2,10],[10,8,3],[7,6,5]])
arr8 = np.array([[2,2,2],[3,3,3],[4,4,4]])
print('陣列arr7：\n',arr7)
print('陣列arr8：\n',arr8)
# 求餘數
print('計算餘數：\n',arr7 % arr8)
# 求整除
print('計算整除：\n',arr7 // arr8)
# 求指數
print('計算指數：\n',arr7 ** arr8)

print(np.modf(arr7/arr8))
# 整除部分
print(np.modf(arr7/arr8)[1])

arr7 = np.array([[1,2,10],[10,8,3],[7,6,5]])
arr8 = np.array([[2,2,2],[3,3,3],[4,4,4]])
print('陣列arr7：\n',arr7)
print('陣列arr8：\n',arr8)
# 取子集
# 從arr7中取出arr7大於arr8的所有元素
print('滿足條件的二維陣列元素獲取：\n',arr7[arr7>arr8])
# 從arr9中取出大於10的元素
arr9 = np.array([3,10,23,7,16,9,17,22,4,8,15])
print('滿足條件的一維陣列元素獲取：\n',arr9[arr9>10])

# 判斷操作
# 將arr7中大於7的元素改成5，其餘的不變
print('二維陣列的條件操作：\n',np.where(arr7>7,5,arr7))
# 將arr9中大於10 的元素改為1，否則改為0
print('一維陣列的條件操作：\n',np.where(arr9>10,1,0))

# 各輸入陣列維度一致，對應維度值相等
arr10 = np.arange(12).reshape(3,4)
print(arr10)
arr11 = np.arange(101,113).reshape(3,4)
print(arr11)
print('3×4的二維矩陣運算：\n',arr10 + arr11)

# 各輸入陣列維度不一致，對應維度值相等
arr12 = np.arange(60).reshape(5,4,3)
print(arr12)
arr10 = np.arange(12).reshape(4,3)
print(arr10)
print('維數不一致，但末尾的維度值一致：\n',arr12 + arr10)

# 各輸入陣列維度不一致，對應維度值不相等，但其中有一個為1
arr12 = np.arange(60).reshape(5,4,3)
print(arr12)
arr13 = np.arange(4).reshape(4,1)
print(arr13)
print('維數不一致，維度值也不一致，但維度值至少一個為1：\n',arr12 + arr13)
# 加1補齊
arr14 = np.array([5,15,25])
print('arr14的維度自動補齊為(1,3)：\n',arr10 + arr14)

# 一維陣列的點積
vector_dot = np.dot(np.array([1,2,3]), np.array([4,5,6]))
print('一維陣列的點積：\n',vector_dot)

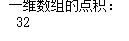
# 二維陣列的乘法
print('兩個二維陣列：')
print(arr10)
print(arr11)
arr2d = np.dot(arr10,arr11)
print('二維陣列的乘法：\n',arr2d)

import numpy as np

# diag的使用
arr15 = np.arange(16).reshape(4,-1)
print('4×4的矩陣：\n',arr15)
print('取出矩陣的主對角線元素：\n',np.diag(arr15))
print('由一維陣列構造的方陣：\n',np.diag(np.array([5,15,25])))
print('由一維陣列構造的方陣：\n',np.diag(np.array(np.diag(arr15))))

# 計算方陣的特徵向量和特徵根
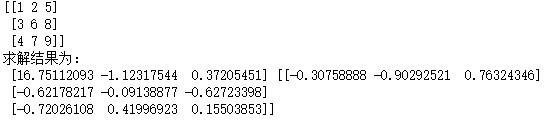
arr16 = np.array([[1,2,5],[3,6,8],[4,7,9]])
print(arr16)
a,b = np.linalg.eig(arr16)
print('求解結果為：\n',a,b)

# 計算偏回歸係數
X = np.array([[1,1,4,3],[1,2,7,6],[1,2,6,6],[1,3,8,7],[1,2,5,8],[1,3,7,5],[1,6,10,12],[1,5,7,7],[1,6,3,4],[1,5,7,8]])
print(X)
print(X.shape)
Y = np.array([3.2,3.8,3.7,4.3,4.4,5.2,6.7,4.8,4.2,5.1])
print(Y)
print(Y.shape)
X_trans_X_inverse = np.linalg.inv(np.dot(np.transpose(X),X))
print(X_trans_X_inverse)
beta = np.dot(np.dot(X_trans_X_inverse,np.transpose(X)),Y)
print('偏回歸係數為：\n',beta)

# 多元線性方程組
A = np.array([[3,2,1],[2,3,1],[1,2,3]])
print(A)
b = np.array([39,34,26])
print(b)
X = np.linalg.solve(A,b)
print('三元一次方程組的解：\n',X)

# 範數的計算
arr17 = np.array([1,3,5,7,9,10,-12])
print(arr17)
# 一範數
res1 = np.linalg.norm(arr17, ord = 1)
print('向量的一範數：\n',res1)
# 二範數
res2 = np.linalg.norm(arr17, ord = 2)
print('向量的二範數：\n',res2)
# 無窮範數
res3 = np.linalg.norm(arr17, ord = np.inf)
print('向量的無窮範數：\n',res3)

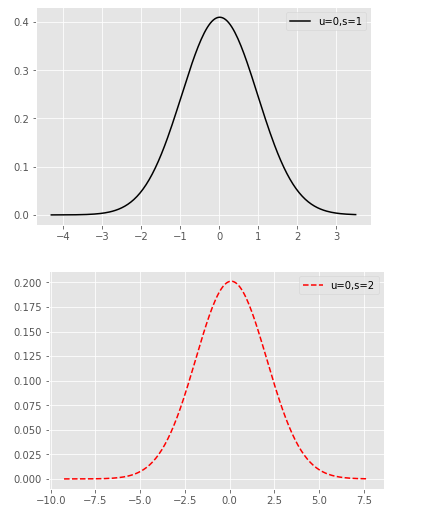
import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats

# 生成各種正態分佈隨機數
np.random.seed(1234)
rn1 = np.random.normal(loc = 0, scale = 1, size = 1000)
print(rn1.shape)
rn2 = np.random.normal(loc = 0, scale = 2, size = 1000)
print(rn2.shape)
rn3 = np.random.normal(loc = 2, scale = 3, size = 1000)
print(rn3.shape)
rn4 = np.random.normal(loc = 5, scale = 3, size = 1000)
print(rn4.shape)
# 繪圖
plt.style.use('ggplot')
sns.distplot(rn1, hist = False, kde = False, fit = stats.norm, fit_kws = {'color':'black','label':'u=0,s=1','linestyle':'-'})
# 呈現圖例
plt.legend()
plt.show()

sns.distplot(rn2, hist = False, kde = False, fit = stats.norm, fit_kws = {'color':'red','label':'u=0,s=2','linestyle':'--'})
# 呈現圖例
plt.legend()
plt.show()
sns.distplot(rn3, hist = False, kde = False, fit = stats.norm, fit_kws = {'color':'blue','label':'u=2,s=3','linestyle':':'})
# 呈現圖例
plt.legend()
plt.show()

sns.distplot(rn4, hist = False, kde = False, fit = stats.norm, fit_kws = {'color':'purple','label':'u=5,s=3','linestyle':'-.'})
# 呈現圖例
plt.legend()
plt.show()

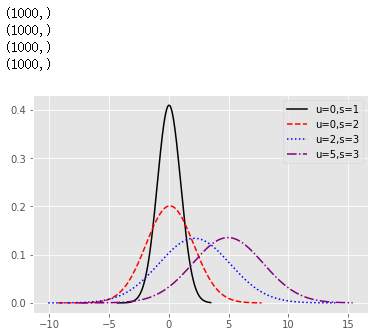
import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats

# 生成各種正態分佈隨機數
np.random.seed(1234)
rn1 = np.random.normal(loc = 0, scale = 1, size = 1000)
print(rn1.shape)
rn2 = np.random.normal(loc = 0, scale = 2, size = 1000)
print(rn2.shape)
rn3 = np.random.normal(loc = 2, scale = 3, size = 1000)
print(rn3.shape)
rn4 = np.random.normal(loc = 5, scale = 3, size = 1000)
print(rn4.shape)
# 繪圖
plt.style.use('ggplot')
sns.distplot(rn1, hist = False, kde = False, fit = stats.norm, fit_kws = {'color':'black','label':'u=0,s=1','linestyle':'-'})
sns.distplot(rn2, hist = False, kde = False, fit = stats.norm, fit_kws = {'color':'red','label':'u=0,s=2','linestyle':'--'})
sns.distplot(rn3, hist = False, kde = False, fit = stats.norm, fit_kws = {'color':'blue','label':'u=2,s=3','linestyle':':'})
sns.distplot(rn4, hist = False, kde = False, fit = stats.norm, fit_kws = {'color':'purple','label':'u=5,s=3','linestyle':'-.'})
# 呈現圖例
plt.legend()
plt.show()

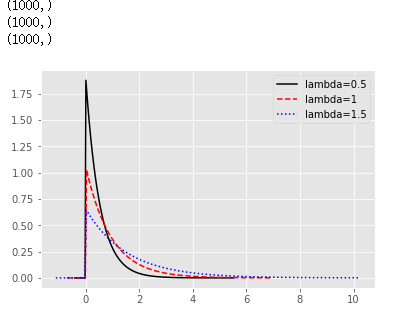
# 生成各種指數分佈隨機數
np.random.seed(1234)
re1 = np.random.exponential(scale = 0.5, size = 1000)
re2 = np.random.exponential(scale = 1, size = 1000)
re3 = np.random.exponential(scale = 1.5, size = 1000)
print(re1.shape)
print(re2.shape)
print(re3.shape)
# 繪圖
sns.distplot(re1, hist = False, kde = False, fit = stats.expon,
fit_kws = {'color':'black','label':'lambda=0.5','linestyle':'-'})
sns.distplot(re2, hist = False, kde = False, fit = stats.expon,
fit_kws = {'color':'red','label':'lambda=1','linestyle':'--'})
sns.distplot(re3, hist = False, kde = False, fit = stats.expon,
fit_kws = {'color':'blue','label':'lambda=1.5','linestyle':':'})
# 呈現圖例
plt.legend()
# 呈現圖形
plt.show()