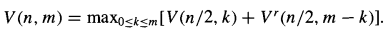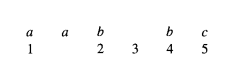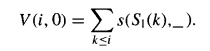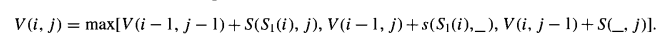入門生物資訊學，選了一條比較難的路，直接從底層演算法開始，這種做法其實不太明智。讀了"Algorithms on Strings, Trees and Sequences"，一本厚厚的演算法書，後半部分其實讀得有些粗糙。今天讀完了第一遍，總的來說還是有些收穫，將筆記記錄於此。

全書總共分為四部分：基本字串演算法、字尾樹演算法、非精確匹配演算法、對映與測序。基本字串演算法以KMP為代表，這個是基本功，而且很久之前的部落格竟然正好記錄了這個演算法；字尾樹演算法在前幾篇部落格專門進行了描述；非精確匹配以動態規劃為基礎，這個也算是老朋友，近期的部落格也專門討論了這個主題，本文也將繼續延伸這個話題；對映與測序，也將在此進行討論。因此本文分為兩大部分：非精確匹配的進一步討論、對映與測序。

整理得有點亂，甚至有些部分直接用的截圖，以後有機會再進一步整理。本文的主要目的是記錄一些核心思路，方便今後回顧。

 

非精確匹配的進一步討論

Refining Core String Edits and Alignments

空間優化：Computing alignments in only linear space

那麼轉移方程可以寫成如下形式：

由轉移方程可知，空間可壓縮一維。

 

時間優化：Faster algorithms when the number of differences is bounded 

之前在後綴樹的應用裡討論過 k-mismatch的問題，這裡講討論 k-difference 的問題，區別在於：前者只允許替換，而後者還允許增刪。

兩類特殊的 k-difference問題：

k-difference global alignment 

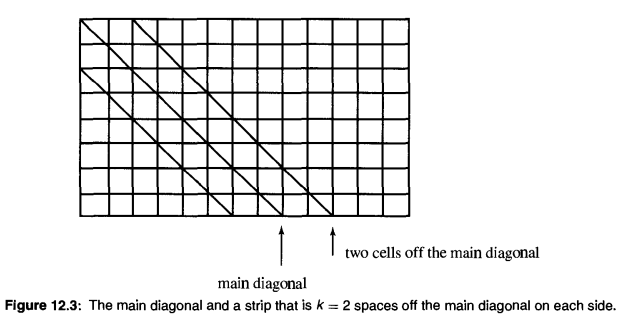
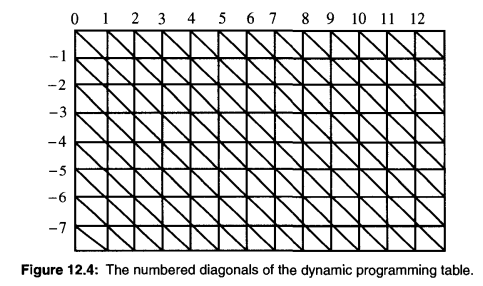
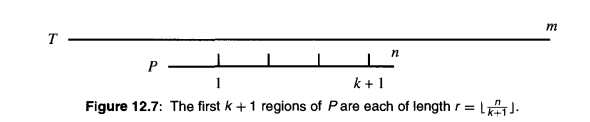
下圖為動態規劃轉移表，(0, 0)開始的對角線為主對角線，其左下方的為負對角線，其右上方的為正對角線。若最多允許k 個不同，則最終結果必然從 -k對角線 至 k對角線 之間的條帶中的狀態推導而來，因為這個條帶以外的狀態，其匹配已經出現了超過k個不同的字元。

 

Exclusion methods: fast expected running time 

先排除一些不可能匹配成功的片段，進而優化計算速度。總的思路如下：

具體的演算法很多，這裡描述兩個典型的：BYP演算法、CL演算法。

BYP演算法：

 

CL演算法：

 

Yet more suffix trees and more hybrid dynamic programming 

有兩個典型的問題。

The P-against-all problem Given strings P and T, compute the edit distance between P and every substring T' of T. 

The threshold all-against-all problem Given strings P and T and a threshold d, find every pair of substrings P' of P and T' of T such that the edit distance between P' and T' is less than d. 

思路：

對於P-against-all 問題，可以先構建出T的字尾樹，在這個字尾樹上計算與P的編輯距離，即在後綴樹上進行深度優先的動態規劃。優點在於可以省去很多重複計算。對於all-against-all 問題，請參考書上相關章節（12.4.2）。

 

LCS 的快速演算法

其實就是將LCS 問題轉化為LIS 問題，而LIS 可以在O(N*logN) 內實現，因此LCS 也變成了O(N*logN)。

LIS的O(N*logN)演算法

D為數字序列，D的一個cover定義為D的下降序列的集合，且這個集合涵蓋了S的序列全部。cover的大小為這個集合中下降序列的個數。

如：S= 5, 3, 4, 9, 6, 2, 1, 8, 7, 10。則 {5, 3, 2, 1}; {4}; {9, 6}; {8, 7}; {10} 是S 的一個cover，這個cover的大小為5。

根據定理12.5.4可知，構建最小cover的過程可以採用二分搜尋法，因此最終的時間複雜度為O(N*logN)。

 

如何將LCS 問題轉歸為LIS 問題

定義：r(i)表示S1[i]這個字元 在S2中出現過多少次，r=∑r(i)。

定義：t(x)表示x 這個字元在S2 中出現的位置的列表，並且順序為從大到小排列。

舉例：S1=abacx， S2=baabca，則 r=3+2+3+1+0=9，t(a)=(6,3,2)，t(b)=(4,1)。

基於S1構建列表SS：對於S1中每個位置i，用t(S1[i])列表進行替換，最終可以得到長度為r的新列表SS。

舉例：對於以上S1和S2，構建的SS為：（6,3,2,4,1,6,3,2,5）。

定理：SS的LIS 與S1和S2的LCS對應。

 

拓展：多個字串的LCS問題，可以用類似的方法轉換成LIS問題。

 

Extending the Core Problem

主要討論了3個問題：Parametric sequence alignment 、Computing suboptimal alignments  和 Chaining diverse local alignments。此處主要看下 Parametric sequence alignment。

實際工作中，會遇到不少帶引數的字串匹配問題。

 

Multiple String Comparison

將字串對齊問題（非精確匹配）從2個字串拓展到多個字串，即為多字串比較問題。實際上從生物學角度來看，多個字串的問題與兩個字串的問題是相反的。

兩個生物學事實。

The first fact of biological sequence analysis: In biomolecular sequences (DNA, RNA, or amino acid sequences), high sequence similarity usually implies significant functional or structural similarity. 

The second fact of biological sequence comparison: Evolutionarily and functionally related molecular strings can differ significantly throughout much of the string and yet preserve the same three-dimensional structure(s), or the same two-dimensional substructure(s) (motifs, domains), or the same active sites, or the same or related dispersed residues (DNA or amino acid). 

第一個事實是兩個字串問題的生物學基礎，第二個事實是間隔問題及多個字串問題的生物學基礎。

Multiple String Comparison的3大應用：蛋白家族（及超級家族）的呈現、DNA或蛋白質中與結構（或功能）相關的保守片段的識別和呈現、DNA或蛋白質的進化史的推導（進化樹的形式呈現）（進化樹的內容本文略去）。

 

Family and superfamily representation

常用的呈現方式有3種：profile representations, consensus sequence representations, and signature representations. 

 

profile representations

定義：Given a multiple alignment of a set of strings, a profile for that multiple alignment specifies for each column the frequency that each character appears in the column. A profile is sometimes also called a weight matrix in the biological literature. 

舉例：下圖是對齊後的結果。

對每列的各個字元計算出現頻率，得到下表，即為profile representations。

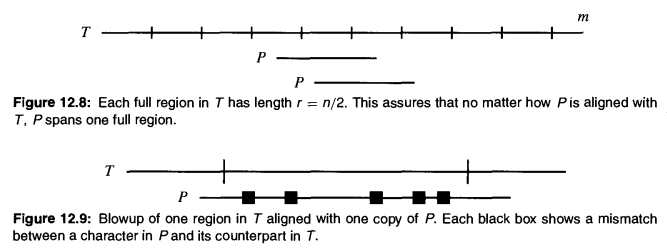
對於新字串aabbc，其相對於profile的最佳對齊方式應當如下圖所示。

解決思路：

For a character y and column j, let p(y, j) be the frequency that character y appears in column j of the profile, and let S(x, j) denote ∑y[s(x, y) x p(y, j)], the score for aligning x with column j. 

Let V(i, j) denote the value of the optimal alignment of substring S[l..i] with the first j columns of C. 

初始條件：

 

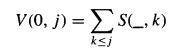
轉移方程：

 

signature representations

一些保守序列可以用類似於正則表示式的形式表示，這種表示即為signature representations。如某個motif 可表示如下：

[&H][&A]D[DE]xn[TSN]x4[QK]Gx7[&A]

"&" stands for any amino acid from the group (/, L,V, M, F, Y, W), "x" stands for any amino acid, and alternative amino acids are bracketed together. The subscript on x gives the length of a permitted substring; "n" indicates that any length substring is possible. 

 

consensus sequence representations

找一個公認的有代表性序列，作為該蛋白家族的呈現，即為consensus sequence representations。

Steiner consensus strings 

D(Si, Sj) denotes the weighted edit distance of strings Si, and Sj. 

Given a set of strings S, and given another string S', the consensus error of a string S' relative to S is E(S') = ∑si∈s D(S' Si). Note that S' need not be from S. 

Given a set of strings S, an optimal Steiner string S* for <S is a string that minimizes the consensus error E(S*) over all possible strings. 

 

Multiple string alignments 的計算

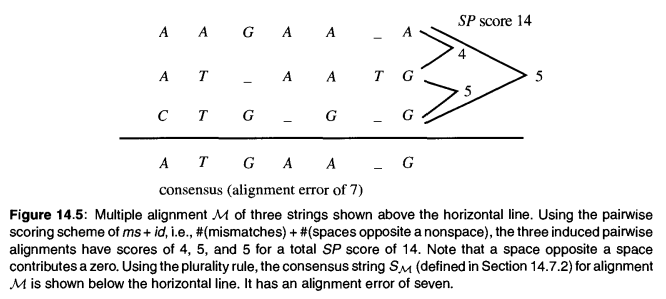
給定一種對齊方式，對於其中任意兩個字串計算分值，最後將所有分值求和，得到總分值SP（sum of pairs），目標是使得SP最小化。

這個問題雖然可以使用動態規劃準確求解，但是時間複雜度是指數級的，這是個NP 完全問題。書上給出了三個字串的SP求解示例程式（pascal語言）。

此外，書中還給出了bounded-error approximation 的方法（界定誤差的近似求法）——center star法。感興趣的請直接參考章節14.6.2。

 

Sequence Databases and Their Uses

這個部分介紹了常見的幾個資料庫 及其背後的部分演算法，如：FASTA、BLAST、PAM、BLOCKS和BLOSUM 等。

本文此處不進行記錄，直接看書吧，或者在實際操作中去領會。

 

對映與測序

Mapping

概念

以下概念摘自網路資源（具體來源不詳）。

遺傳圖譜（genetic maps）：某一物種的染色體圖譜（也就是我們所知的連鎖圖譜），顯示所知的基因和/或遺傳標記的相對位置，而不是在每條染色體上特殊的物理位置。採用遺傳學分析方法將基因或其它DNA標記按一定的順序排列在染色體上，這一方法包括雜交實驗，家系分析。標記間的距離（遺傳圖距）用減數分裂中的交換頻率來表示，單位為釐摩Centi-Morgan, cM), 每單位釐摩定義為1%交換率。遺傳學圖譜的解像度（解析度）低，大約只能達到100萬鹼基對(1Mb)的水平。

物理圖譜（physical maps）：顧名思義，是DNA中一些可識別的界標（如限制性酶切位點、基因等）在DNA上的物理位置，圖距是物理長度單位，如染色體的帶區、核苷酸對的數量等。

兩者異同：
　　①遺傳圖譜是基於重組頻率，物理圖譜是基於直接測量的DNA結構。
　　②減數分裂重組的頻率並不統一沿大多數染色體。有一些熱點和冷點在重組和/或突變。熱點和冷點會導致相當大的格律失真時，遺傳圖譜和物理地圖並排排列時。
　　③遺傳圖譜表示的是基因或標記間的相對距離，以重組值表示，單位CM
　　④物理圖譜表示的是基因或標記間的物理距離，距離的單位為長度單位，如μm或者鹼基對數（bp或kp）等。

簡而言之，前者是描述的基因相對位置,後者是具體的鹼基位置。

STS是序列標記位點（sequence-tagged site）的縮寫，是指染色體上位置已定的、核苷酸序列已知的、且在基因組中只有一份拷貝的DNA短片斷，一般長200bp－500bp。它可用PCR方法加以驗證。將不同的STS依照它們在染色體上的位置依次排列構建的圖為STS圖。在基因組作圖和測序研究時，當各個實驗室發表其DNA測序資料或構建成的物理圖時，可用STS來加以鑑定和驗證，並確定這些測序的DNA片段在染色體上的位置；還有利於彙集分析各實驗室發表的資料和資料，保證作圖和測序的準確性。

EST是表達序列標籤（expressed sequence tag）的縮寫，在人類基因組測序工作中，有一個區別於"全基因組戰略"的"cDNA戰略"，即只測定轉錄的DNA序列。此時，須從cDNA文庫中獲取一些長為300－400各鹼基序列作為表達序列標籤，其作用相當於全基因組測序時的序列標記位點（STS），即可用來驗證和整理不同實驗室發表的cDNA測序資料。兩端又重疊序列的EST可以裝配成全長的cDNA序列。特定的EST序列有時可代表特定的cDNA。

輻射性雜交製圖技術（radiation-hybrid mapping）是一種體細胞雜交技術，適用於構建人類基因組長範圍內的高解析度連續物理圖譜。利用高劑量的X射線將候選染色體打斷成若干片段，含有這種片段的細胞可與倉鼠細胞形成雜交克隆。在這種雜交中，人類染色體片段被插入到倉鼠染色體的中間部分，因此大部分克隆片段在進行有絲分裂時處於穩定的狀態。

利用類似於遺傳重組原理和最大似然性的統計學方法來計算存在於DNA片段上的多型性或非多型性標記之間的斷點頻率，以此估計標記之間的距離，並建立人類基因組拷貝庫---體細胞雜交系統。可根據不同要求構建出斷裂程度不同的多套拷貝，從而得到不同解析度的放射雜交圖。總之，輻射性雜交是建立在受到X射線照射的供體細胞與非放射線處理的受體細胞融合基礎上的一種體細胞遺傳學方法。

Physical mapping：STS-content mapping and ordered clone libraries

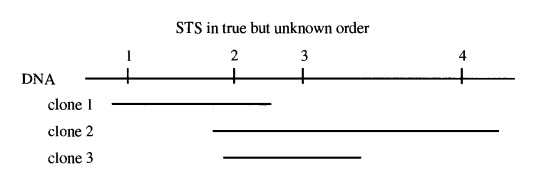
下圖中有4個STS，其真實順序如下圖所示，但是這個順序我們事先是不知道的，需要結合後面的計算去推斷出來。下圖還包含3個clone片段。

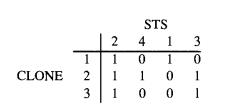
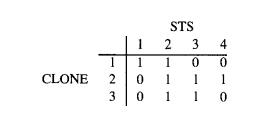
匹配出3個片段各自包含了哪些STS之後，可得到下圖的01矩陣，由於事先並不知道各個STS的排列順序，因此此時順序是打亂的。

找出一種排列順序，使得每行中的1具有連續性，成為一個獨立的塊。這也就實現了STS順序的重建。

Physical mapping: radiation-hybrid mapping 

這個是加強版的STS順序問題，每個細胞具有多個不相鄰的片段，如下圖所示。

由於不知道真實順序，匹配各個STS後，得到以下的01矩陣。

重建STS順序的方法：traveling salesman tour。

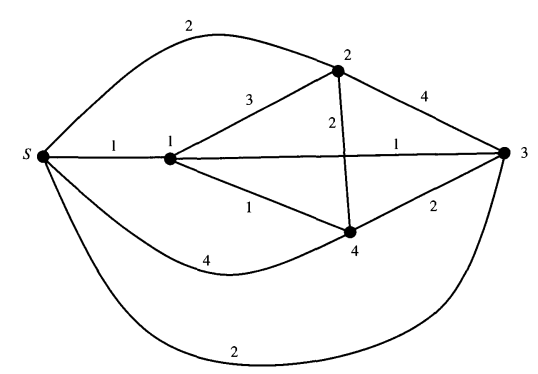
構建無向圖，邊 e(u ,v)表示編號為u與v的STS 列，之間有幾個01值不相同。為了方便起見，此處略去5-7這3個STS，構建的無向圖如下所示。

找一個從S出發且經歷所有節點的路徑，且經歷的路徑總長度（即所有e(u ,v)之和）最短，這條路徑的順序很可能就是STS的順序。上圖求得的最短路徑為：S-3-1-4-2，長度為6，對應的連續塊的數量為4。遺憾的是並不是真實的順序1234（真實順序的連續塊的數量竟然更大…）。（期待更好的方法解決這個問題）

Physical mapping: fingerprinting for general map construction 

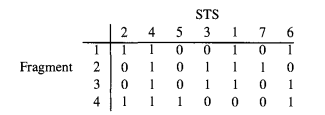
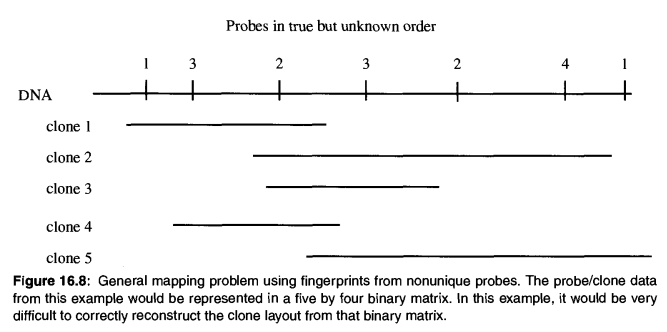
探針問題與STS問題類似，但是探針在DNA序列中可以重複出現，如下圖所示。

上圖最終構造的01矩陣是5*4的規模，重建出其真實順序的難度比較大。有不少文章提出過解決方案，書中描述了一種貪心方法，請參考章節16.8。

 

Sequencing

引物步移（primer walking）：一種長鏈DNA測序的策略。根據已測出的序列結構設計測序引物，按第一輪測序得出的新序列，再設計引物進行第二輪測序，如此重複，直至獲得全序列。

巢狀缺失法（Nested deletion） : 該法基本原理是基因DNA鏈的一端與載體相連固定,另一端在核酸外切酶的作用下隨著時間的延長,較勻速地消化變短。這樣可人為獲得一組長度不等(如依次相差200～250 bp)的從一端開始缺失的DNA片段。它們從缺失端開始的測序可讀部分宛如拉桿天線的一段套管,最長片段(未被核酸外切酶作用的DNA)相當於拉桿天線的全長,它的可讀部分相當於拉桿天線的最遠端的套管。這些DNA片段從長至短雖然依次相差200～250 bp,但從缺失端可讀取300～500 bp序列,重疊部分便可準確無誤地將相鄰段重合拼接。測序中,它們的引物相同因而可以很方便地首先讀出引物序列,找出該DNA片段的起始,起始段DNA序列也正是前一較長DNA片段可讀的後一部分序列,它們如此重疊巢狀,便可準確測出整個基因(或長DNA鏈)的序列。

書中還提到了 "Top-down, bottom-up sequencing( the picture using YACs)" 、"Shotgun DNA sequencing" 等方法的描述。這些東西將會重新學習一遍，之後會系統地學一下WGS的知識。

 

----------------------------------------------------------------------------------

2018/10/02 補充

學習路上吃了很多虧，無法及時的將所學的東西運用起來。時間不夠用啊，我的專業不是這個方向，有很多事情等著我去做呢，這個時候最高效的方式是先了解如何使用，然後練習即可。學有餘力再去專研其理論知識（人生苦短）。以今天的經驗教訓來看，本文的這些東西（包括之前字串的非精確匹配、3篇字尾樹系列部落格），以後不要再糾結了，儘量不要把時間花在這方面。