分治演算法入門
阿新 • • 發佈:2018-12-04
https://blog.csdn.net/rainchxy/article/details/78957851可以看這篇部落格
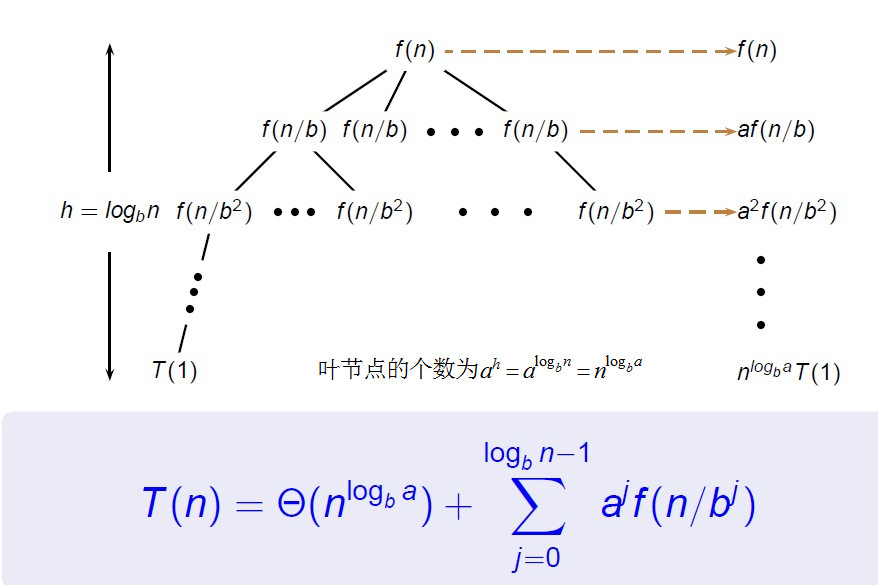
分治的複雜度分析:對於規模為n的問題,將其分成a個子問題,每個問題的規模是n/b。

證明:在遞推式中每次往下分治時,子問題數量都會乘以a,子問題規模都會除以b,那麼當子問題規模到達1時,子問題數量就是a^logb(n)、即n^logb(a)
f(n)是子問題向上合併的代價,每次往下分治時,merge的代價是其問題數量*合併當前規模的問題的代價,當分治到問題規模是1時,向上合併的代價就是a^logb(n)-1 + ... + af(n/b) + f(n),

有上述推導式可以得知分治演算法的複雜度只看兩個因子,一是n^logb(a),二是sum{ aj * f(n/bj) },0<=j<=logb(n)-1,用等比數列的級數求和算出最終複雜度即可
對應如下遞迴樹
casr1: 當f(n)<O(n^logb(a))時,假設f(n)=O(n^(logb(a)-e)),e>0,
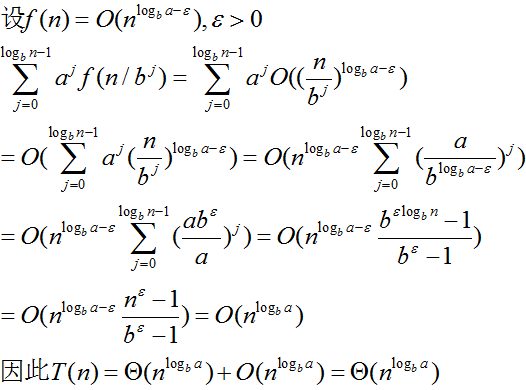
遞迴樹的每層成本從根向下呈幾何級數增長,成本在葉節點一層達到最高,即最後一次遞迴是整個過程中成本最高的一次,故其占主導地位。所以遞迴分治的總成本在漸進趨勢上和葉子層的成本一樣。 此情況下分治代價由樹的葉子節點代價決定
case 2:當f(n)=O(n^logb(a))時,假設f(n)=O(n^logb(a))
 遞迴樹每層的成本在漸進趨勢上一樣,此情況下分治代價均勻分佈在樹的各層上
遞迴樹每層的成本在漸進趨勢上一樣,此情況下分治代價均勻分佈在樹的各層上
case 3:f(n)>O(n^logb(a)),
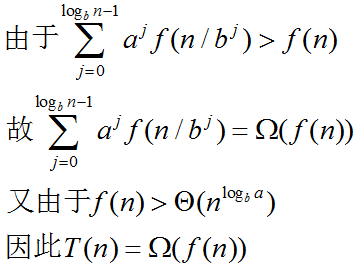 遞迴樹每層成本呈幾何級數遞減,樹根一層的成本占主導地位。因此,總成本就是樹根層的成本。分治代價集中在根的代價上
遞迴樹每層成本呈幾何級數遞減,樹根一層的成本占主導地位。因此,總成本就是樹根層的成本。分治代價集中在根的代價上
