LSM樹（Log-Structured Merge Tree）儲存引擎

代表資料庫：nessDB、leveldb、hbase，kudu等

核心思想的核心就是放棄部分讀能力，換取寫入的最大化能力。LSM Tree ，這個概念就是結構化合並樹的意思，它的核心思路其實非常簡單，就是假定記憶體足夠大，因此不需要每次有資料更新就必須將資料寫入到磁碟中，而可以先將最新的資料駐留在磁碟中，等到積累到最後多之後，再使用歸併排序的方式將記憶體內的資料合併追加到磁碟隊尾(因為所有待排序的樹都是有序的，可以通過合併排序的方式快速合併到一起)。

日誌結構的合併樹（LSM-tree）是一種基於硬碟的資料結構，與B-tree相比，能顯著地減少硬碟磁碟臂的開銷，並能在較長的時間提供對檔案的高速插入（刪除）。然而LSM-tree在某些情況下，特別是在查詢需要快速響應時效能不佳。通常LSM-tree適用於索引插入比檢索更頻繁的應用系統。Bigtable在提供Tablet服務時，使用GFS來儲存日誌和SSTable，而GFS的設計初衷就是希望通過新增新資料的方式而不是通過重寫舊資料的方式來修改檔案

磁碟的技術特性:對磁碟來說，能夠最大化的發揮磁碟技術特性的使用方式是:一次性的讀取或寫入固定大小的一塊資料，並儘可能的減少隨機尋道這個操作的次數。

轉自：http://blog.csdn.net/dbanote/article/details/8897599

LSM樹是Hbase裡非常有創意的一種資料結構，它和傳統的B+樹不太一樣，下面先說說B+樹。

1 B+樹

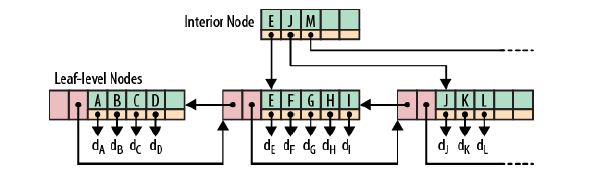
相信大家對B+樹已經非常的熟悉，比如Oracle的普通索引就是採用B+樹的方式，下面是一個B+樹的例子：

根節點和枝節點很簡單，分別記錄每個葉子節點的最小值，並用一個指標指向葉子節點。

葉子節點裡每個鍵值都指向真正的資料塊（如Oracle裡的RowID），每個葉子節點都有前指標和後指標，這是為了做範圍查詢時，葉子節點間可以直接跳轉，從而避免再去回溯至枝和跟節點。

B+樹最大的效能問題是會產生大量的隨機IO，隨著新資料的插入，葉子節點會慢慢分裂，邏輯上連續的葉子節點在物理上往往不連續，甚至分離的很遠，但做範圍查詢時，會產生大量讀隨機IO。

對於大量的隨機寫也一樣，舉一個插入key跨度很大的例子，如7->1000->3->2000 ... 新插入的資料儲存在磁碟上相隔很遠，會產生大量的隨機寫IO.

從上面可以看出，低下的磁碟尋道速度嚴重影響效能（近些年來，磁碟尋道速度的發展幾乎處於停滯的狀態）。

2 LSM樹

為了克服B+樹的弱點，HBase引入了LSM樹的概念，即Log-Structured Merge-Trees。

為了更好的說明LSM樹的原理，下面舉個比較極端的例子：

現在假設有1000個節點的隨機key，對於磁碟來說，肯定是把這1000個節點順序寫入磁碟最快，但是這樣一來，讀就悲劇了，因為key在磁碟中完全無序，每次讀取都要全掃描；

那麼，為了讓讀效能儘量高，資料在磁碟中必須得有序，這就是B+樹的原理，但是寫就悲劇了，因為會產生大量的隨機IO，磁碟尋道速度跟不上。

LSM樹本質上就是在讀寫之間取得平衡，和B+樹相比，它犧牲了部分讀效能，用來大幅提高寫效能。

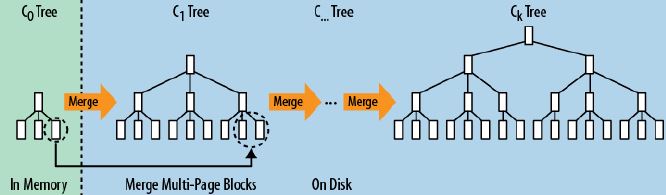
它的原理是把一顆大樹拆分成N棵小樹， 它首先寫入到記憶體中（記憶體沒有尋道速度的問題，隨機寫的效能得到大幅提升），在記憶體中構建一顆有序小樹，隨著小樹越來越大，記憶體的小樹會flush到磁碟上。當讀時，由於不知道資料在哪棵小樹上，因此必須遍歷所有的小樹，但在每顆小樹內部資料是有序的。

以上就是LSM樹最本質的原理，有了原理，再看具體的技術就很簡單了。

1）首先說說為什麼要有WAL（Write Ahead Log），很簡單，因為資料是先寫到記憶體中，如果斷電，記憶體中的資料會丟失，因此為了保護記憶體中的資料，需要在磁碟上先記錄logfile，當記憶體中的資料flush到磁碟上時，就可以拋棄相應的Logfile。

2）什麼是memstore, storefile？很簡單，上面說過，LSM樹就是一堆小樹，在記憶體中的小樹即memstore，每次flush，記憶體中的memstore變成磁碟上一個新的storefile。

3）為什麼會有compact？很簡單，隨著小樹越來越多，讀的效能會越來越差，因此需要在適當的時候，對磁碟中的小樹進行merge，多棵小樹變成一顆大樹。

關於LSM Tree，對於最簡單的二層LSM Tree而言，記憶體中的資料和磁碟中的資料merge操作，如下圖

下面說說詳細例子:

LSM Tree弄了很多個小的有序結構，比如每m個數據，在記憶體裡排序一次，下面100個數據，再排序一次……這樣依次做下去，就可以獲得N/m個有序的小的有序結構。

在查詢的時候，因為不知道這個資料到底是在哪裡，所以就從最新的一個小的有序結構裡做二分查詢，找得到就返回，找不到就繼續找下一個小有序結構，一直到找到為止。

很容易可以看出，這樣的模式，讀取的時間複雜度是(N/m)*log2N 。讀取效率是會下降的。

這就是最本來意義上的LSM tree的思路。那麼這樣做，效能還是比較慢的，於是需要再做些事情來提升，怎麼做才好呢？

LSM Tree優化方式：

a、Bloom filter: 就是個帶隨即概率的bitmap,可以快速的告訴你，某一個小的有序結構裡有沒有指定的那個資料的。於是就可以不用二分查詢，而只需簡單的計算幾次就能知道資料是否在某個小集合裡啦。效率得到了提升，但付出的是空間代價。

b、compact:小樹合併為大樹:因為小樹他效能有問題，所以要有個程序不斷地將小樹合併到大樹上，這樣大部分的老資料查詢也可以直接使用log2N的方式找到，不需要再進行(N/m)*log2n的查詢了